Произвольные выражения векторной алгебры
Федеральное государственное образовательное бюджетное учреждение
Высшего образования
«ФИНАН
«ФИНАНСОВЫЙ УНИВЕРСИТЕТ ПРИ ПРАВИТЕЛЬСТВЕ
РОССИЙСКОЙ ФЕДЕРАЦИИ»
Департамент анализа данных, принятия решений и финансовых технологий
С.А.Зададаев
Векторная алгебра (R S tudio)
Учебно-методические рекомендации для проведения
семинара №27 по компьютерному практикуму
Для бакалавров направления 38.03.01 «Экономика»
Электронное издание
Москва 2017
Векторная алгебра (R S tudio)
В этом разделе мы рассмотрим большинство операций, связанных с арифметическими векторами.
Задание. Для векторов
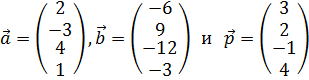
вычислить следующие выражения:
a)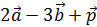 
– линейная комбинация векторов
b)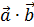 
и 
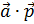– скалярное произведение векторов
c)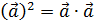 
– квадрат вектора
d) a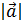 
, b 
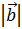и p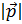 
– длины векторов
e) cosa , b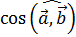 
– косинус угла между векторами a 
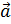и b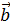 
f) 2 a , b ∙ p +3 b ∙ p 2 - b ∙ b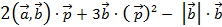 
– сложное выражение векторной алгебры
Решение. Подробно разберем каждую из перечисленных операций векторной алгебры, но сначала образуем в R указанные три вектора:
a <- c(2, -3, 4, 1) # Сформировать вектор a из набора чисел 2, -3, 4, 1
b <- c(-6, 9, -12, -3) # Сформировать вектор b из набора чисел -6, 9, -12, -3
p <- c(3, 2, -1, 4) # Сформировать вектор a из набора чисел 3, 2, -1, 4
a; b; p # Смотрим результат
Не забываем выделить этот фрагмент и кликнуть мышкой по кнопке меню Run или нажать сочетание клавиш Ctrl + Enter. Обязательно проверьте отчет компилятора в нижнем окне консоли на предмет ошибок ввода векторов:
|
|
|
> a; b; p
[1] 2 -3 4 1
[1] -6 9 -12 -3
[1] 3 2 -1 4
Линейная комбинация векторов
a) вычислить 2 a -3 b + p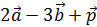
Для вычисления подобных выражений, называемых линейными комбинациями из-за того, что векторы складываются друг с другом и/или умножаются на числа, достаточно просто записать аналогичную строчку в R:
2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации
с результатом в консоли:
> 2*a-3*b+p # Вычисление вектора, равного указанной линейной комбинации векторов[1] 25 -31 43 15Напомним, что линейные операции над векторами осуществляются покоординатно, т.е. в нашем случае должен получиться вектор
2 a 1 -3 b 1 + p 1 ; 2 a 2 -3 b 2 + p 2 ;…; 2 a 4 -3 b 4 + p 4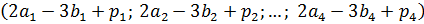 
Попробуйте проверить этот результат вручную.
Скалярное произведение векторов
b) вычислить a ∙ b 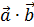и a ∙ p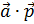
В отличие от предыдущего пункта, здесь нельзя составить обычное умножение векторов, т.к. компилятор R покоординатно перемножит векторы, что не является скалярным произведением. Вообще, важно различать покоординатное произведение векторов (не используется в векторной алгебре, но удобно в программировании):
|
|
|
a 1 b 1 ; a 2 b 2 ;…; a n b n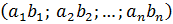 
и скалярное произведение векторов (то что нам сейчас нужно):
a ∙ b = a 1 b 1 + a 2 b 2 +…+ a n b n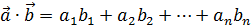 
.
Как видите, в результате получается не вектор, а число (скаляр) – отсюда и название скалярное произведение. Желая подчеркнуть эту разницу в линейной алгебре часто используют круглые скобки для обозначения скалярного произведения: a ∙ b = a ; b .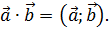 
В языке R эти два приёма программируется следующим образом:
a*b # Покоординатное произведение векторов (не скалярное произведение!)
a%*%b # Скалярное произведение векторов
с результатом:
> a*b # Покоординатное произведение векторов (не скалярное произведение!)[1] -12 -27 -48 -3> a%*%b # Скалярное произведение векторов [,1][1,] -90Обратите внимание, что результат скалярного произведения представлен в виде матрицы 1×1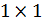 
, т.к. в языке R эта операция интерпретируется как частный случай произведения специальных матриц. Если мы не хотим видеть результат в виде матрицы, мы можем вывести его как обычное число:
as.numeric(a%*%b) # Скалярное произведение векторов
> as.numeric(a%*%b)[1] -90 Аналогично получим скалярное произведение a ∙ p :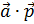
as.numeric(a%*%p) # Скалярное произведение векторов
|
|
|
Кстати, в последнем случае результат оказался равным нулю, что говорит об ортогональности (перпендикулярности) векторов a 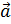и p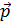 
.
Впрочем, для нахождения скалярного произведения мы могли бы использовать простую конструкцию в виде суммы (sum) попарных произведений координат:
sum(a*p) # Фактически тоже скалярное произведение векторов
с тем же результатом.
с) вычислить a 2 = a ∙ a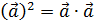
Квадрат вектора a 2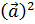 
понимается в векторной алгебре как скалярное произведение самого на себя a ∙ a 
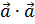, поэтому легко получить:
as.numeric(a%*%a) # Квадрат вектора
> as.numeric(a%*%a) # Квадрат вектора[1] 30Проверьте, что результат, действительно, равен сумме квадратов координат вектора:
a 2 = a ∙ a = a 1 a 1 + a 2 a 2 +…+ a n a n = a 1 2 +… +a n 2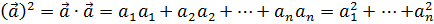 
Замечание. Ошибкой было бы записать a*a или a^2, т.к. в этом случае R выдал бы покоординатное выполнение указанных операций, а не их сумму: (a 1 2 ,… ,a n 2 )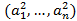 
.
Длина вектора
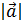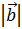d) вычислить a , b и p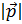
Длиной вектора называют число, равное квадратному корню из a 2 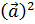и по смыслу это число является длиной отрезка, соединяющего начало и конец вектора, если его интерпретировать как направленный отрезок в евклидовой геометрии:
|
|
|
a = a 1 2 +… +a n 2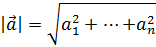 
В языке R получить данное выражение можно несколькими способами. Первый из них – вызвать специальную функцию вычисления нормы элемента для вектора:
norm(a, type="2") # Длина вектора a (обычная евклидова)
с результатом:
> norm(a, type="2") # Длина вектора a (обычная евклидова)[1] 5.477226Второй способ – образовать, согласно формуле, корень из суммы квадратов элементов:
sqrt(sum(a^2)) # Альтернатива: длина вектора a
с тем же результатом:
> sqrt(sum(a^2)) # Альтернатива: длина вектора a[1] 5.477226Аналогично получаем для оставшихся векторов:
norm(b, type="2") # Длина вектора b (обычная евклидова)
sqrt(sum(p^2)) # Альтернатива: длина вектора p
Косинус угла между векторами
e) вычислить cosa,b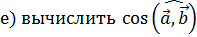 
Воспользуемся формулой для косинуса угла между арифметическими векторами
cosa,b = a∙b a ∙ b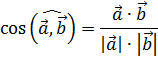 
(a%*%b)/(norm(a, type="2")*norm(b, type="2")) # Косинус угла между a и b
с результатом
> (a%*%b)/(norm(a,type="2")*norm(b,type="2")) [,1][1,] -1 Обратим внимание, что косинус оказался равным –1, что говорит об угле между векторами, равном π.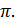 
Это означает, что векторы коллинеарны (параллельны) и противоположно направлены. Кстати, это можно было заметить изначально, т.к. координаты векторов пропорциональны с отрицательным коэффициентом: b =-3 a .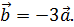 
Конечно, чтобы формула не выглядела громоздкой, ее можно было запрограммировать поэтапно:
ab <- a%*%b # Образуем в переменной ab скалярное произведение векторов a и b
L.a <- norm(a, type="2") # Сохраняем длину вектора a в переменной L.a
L.b <- norm(b, type="2") # Сохраняем длину вектора b в переменной L.b
ab/(L.a*L.b) # Получаем косинус угла
Произвольные выражения векторной алгебры
f) Вычислить 2 a , b ∙ p +3 b ∙ p 2 - b ∙ b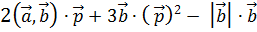 
Вычислим отдельно три слагаемых выражения и образуем из них ответ:
S1 <- 2*as.numeric(a%*%b)*p # Первое слагаемое
S2 <- 3*b*as.numeric(p%*%p) # Второе слагаемое
S3 <- norm(b, type="2")*b # Третье слагаемое
S1 + S2 - S3 # Ответ
c результатом в виде вектора
> S1 + S2 - S3[1] -981.4099 302.1149 -702.8199 -940.7050Обратите внимание, что при вычислении скалярных произведений необходимо конвертировать ответ в число с помощью команды as.numeric(), иначе произойдет несовпадение типов (матрицы и векторы как бы перемешаются в одном выражении) и компилятор R выдаст ошибку.
Если вычисление скалярных произведений производится для многих пар векторов, то для этих целей удобно запрограммировать специальную пользовательскую функцию, скажем, под названием cosV:
cosV <- function(x,y) { # Объявление имени функции cosV двух аргументов
L.x <- norm(x, type="2"); L.y <- norm(y, type="2") # Нахождение длин векторов
cosV <- x%*%y/(L.x*L.y) # Нахождение косинуса угла
return(as.numeric(cosV)) # Возвращение косинуса в качестве значения функции
}
cosV(a,b) # Вызов пользовательской функции cosV
> cosV(a,b) # Вызов пользовательской функции cosV[1] -1
Дата добавления: 2021-05-18; просмотров: 84; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!