Разрешимость задачи анализа потоковых
РАЗДЕЛ 3. ОБНАРУЖЕНИЕ И ПРЕДОТВРАЩЕНИЕ БЛОКИРОВОК РАСПРЕДЕЛЕННЫХ ВЫЧИСЛЕНИЙ
Разметка М-сетей и анализ реализуемости распределенных вычислений
Анализ свойств программ на размеченных графах. Для распознавания и исследования свойств моделей вычислений и программ широко используются различные графы. Метки, присваиваемые дугам или вершинам графа, представляют интересующие семантические свойства, а сама процедура сопоставления дугам и вершинам меток по заданным правилам называется разметкой графа. Разметка, определяемая иногда как анализ информационных потоков (data flow analysis), является процессом сбора информации о свойствах графа, кодируемых элементами (метками) некоторого множества  . В контексте анализа под информационными потоками имеется в виду не только передача операндов (данных), но и управления, синхронизация параллельных процессов и т.д. Далее понятия разметки и анализа графа будут рассматриваться нами как эквивалентные.
. В контексте анализа под информационными потоками имеется в виду не только передача операндов (данных), но и управления, синхронизация параллельных процессов и т.д. Далее понятия разметки и анализа графа будут рассматриваться нами как эквивалентные.
Стандартное окружение для анализа представляет собой следующий набор. Это – структурный граф 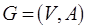 программы с множеством
программы с множеством  вершин и множеством
вершин и множеством  дуг. Вершины, как правило, обозначают операторы программы, а дуги из
дуг. Вершины, как правило, обозначают операторы программы, а дуги из  могут соответствовать передаче данных или управления, а также синхронизации процессов. В некоторых графовых моделях могут присутствовать "разносортные" дуги. Следующий компонент окружения – алгебраическая структура в виде решетки
могут соответствовать передаче данных или управления, а также синхронизации процессов. В некоторых графовых моделях могут присутствовать "разносортные" дуги. Следующий компонент окружения – алгебраическая структура в виде решетки  , нижней
, нижней 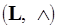 или верхней
или верхней  полуструктуры семантических свойств, где
полуструктуры семантических свойств, где 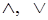 – операции пересечения и объединения на множестве меток (свойств) из
– операции пересечения и объединения на множестве меток (свойств) из  . Третья составляющая – множество
. Третья составляющая – множество  монотонных функций
монотонных функций  , которые называют потоковыми функциями или преобразователями свойств. Функция
, которые называют потоковыми функциями или преобразователями свойств. Функция  монотонна, если
монотонна, если 
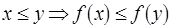 . Здесь
. Здесь 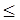 обозначает отношение частичного порядка на
обозначает отношение частичного порядка на  . Наконец, четвертая составляющая окружения для анализа – это частичное отображение
. Наконец, четвертая составляющая окружения для анализа – это частичное отображение  , сопоставляющее подмножествам вершин и дуг графа некоторую монотонную функцию
, сопоставляющее подмножествам вершин и дуг графа некоторую монотонную функцию 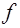 . Потоковая функция
. Потоковая функция  может ассоциироваться с определенной вершиной
может ассоциироваться с определенной вершиной 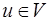 графа
графа  и представлять собой отображение входной информации (меток входящих дуг) в выходную информацию (метки исходящих дуг) вершины
и представлять собой отображение входной информации (меток входящих дуг) в выходную информацию (метки исходящих дуг) вершины  .
.
|
|
|
Пусть 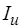 ,
, 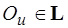 являются метками входа и выхода вершины
являются метками входа и выхода вершины  . Они связаны посредством потоковой функции
. Они связаны посредством потоковой функции  . Часто эту связь представляют так называемым потоковым уравнением вида
. Часто эту связь представляют так называемым потоковым уравнением вида
 , или
, или  , (3.1)
, (3.1)
где  .
.
В (3.1)  – параметры, интерпретируемые следующим образом. Выходная информация
– параметры, интерпретируемые следующим образом. Выходная информация 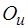 генерируется вершиной
генерируется вершиной  , что обозначается параметром
, что обозначается параметром  , или являются частью входной информации (метка
, или являются частью входной информации (метка 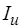 ), сохраняемой при передаче
), сохраняемой при передаче 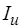 на выход, чему соответствует параметр
на выход, чему соответствует параметр  . Нужно заметить, что в общем случае в (3.1) параметр
. Нужно заметить, что в общем случае в (3.1) параметр  может зависеть от метки
может зависеть от метки 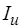 входа вершины
входа вершины  . Информация
. Информация 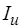 поступает на вход вершины
поступает на вход вершины  от вершин, принадлежащих множеству
от вершин, принадлежащих множеству 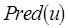 вершин-предшественников
вершин-предшественников  , т.е.
, т.е.
|
|
|
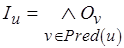 или
или  . (3.2)
. (3.2)
В (3.2) фигурирует операция пересечения или объединения в зависимости от постановки задачи анализа и структуры семантических свойств. Таким образом, с графом связывается система из  потоковых уравнений вида
потоковых уравнений вида
 или
или 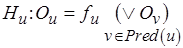 . (3.3)
. (3.3)
Если параметр  не зависит от информации
не зависит от информации 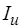 на входе вершины
на входе вершины  , то уравнения (3.3) могут быть записаны в следующем виде:
, то уравнения (3.3) могут быть записаны в следующем виде:
 или
или  . (3.4)
. (3.4)
Разметка графа является стационарной, если свойства его дуг и вершин, определяемые, в частности, системой потоковых уравнений  ,
, 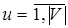 (3.3) или (3.4), не изменяются никаким применением правил разметки. Правило определяет характер замены меток на отдельных этапах анализа. Например, из двух меток некоторой дуги, ранее ей присвоенной
(3.3) или (3.4), не изменяются никаким применением правил разметки. Правило определяет характер замены меток на отдельных этапах анализа. Например, из двух меток некоторой дуги, ранее ей присвоенной 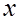 и получаемой на очередном шаге анализа
и получаемой на очередном шаге анализа  , выбирается метка
, выбирается метка 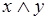 либо метка
либо метка  , где
, где 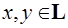 .
.
Известны различные постановки и методы решения задач анализа размеченных графов. Например, заданы: стандартное окружение для анализа 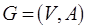 ,
, 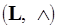 ,
,  ,
,  и некоторая начальная разметка графа
и некоторая начальная разметка графа  . Требуется найти стационарную разметку, при которой свойство любой дуги является наибольшей нижней гранью множества допустимых, в соответствии с правилами разметки, свойств. Задача анализа называется прямой, когда свойства любой вершины определяются свойствами ее предшественников. Если же свойства вершины зависят только от свойств ее преемников, то имеет место обратная задача анализа.
. Требуется найти стационарную разметку, при которой свойство любой дуги является наибольшей нижней гранью множества допустимых, в соответствии с правилами разметки, свойств. Задача анализа называется прямой, когда свойства любой вершины определяются свойствами ее предшественников. Если же свойства вершины зависят только от свойств ее преемников, то имеет место обратная задача анализа.
|
|
|
Многие методы анализа основываются на исключении переменных, однозначно соответствующих меткам. Пусть имеют место два потоковых уравнения:
 ,
,
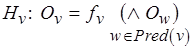 .
.
Исключая переменную  из правой части уравнения
из правой части уравнения  , получаем
, получаем
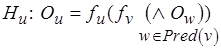 .
.
Это равносильно тому, что в графе исключается дуга  , а вместо нее вводится дуга
, а вместо нее вводится дуга  .
.
Для исключения переменных из рекурсивных уравнений используется операция замыкания, позволяющая найти неподвижную точку уравнения. Пусть, например, свойство вершины  описывается уравнением
описывается уравнением  , где
, где  и
и  – термы, не содержащие переменной
– термы, не содержащие переменной  . Операция замыкания
. Операция замыкания  приводит к уравнению
приводит к уравнению  . Методы вычисления
. Методы вычисления  известны для различных задач анализа. Неподвижная точка
известны для различных задач анализа. Неподвижная точка  существует, если потоковая функция является монотонной, а решетка свойств не содержит бесконечных строго убывающих цепей (последовательность
существует, если потоковая функция является монотонной, а решетка свойств не содержит бесконечных строго убывающих цепей (последовательность  , где
, где  , называется строго убывающей цепью с началом в
, называется строго убывающей цепью с началом в  , если
, если  , где > обозначает отношение частичного порядка на
, где > обозначает отношение частичного порядка на  ).
).
|
|
|
Методы анализа. Кратко рассмотрим ключевые положения, которые лежат в основе двух подходов к анализу графов на основе исключения переменных. Пусть модель вычислений представлена потоковым графом на рис. 3.1, а.
Положим, вершины представляют операторы, а дуги – передачу управления. В графе выделяются две вершины – начальная (В) и конечная (Е). Вершина В представляет точку входа, а вершина Е – точку выхода из программы.
Рассмотрим прямую задачу анализа, когда входная информация любой вершины определяется через объединение свойств выходов вершин-предшественников. Метод так называемого исчерпывающего (exhaustive) анализа позволяет получить такое решение, когда метка выхода вершины  графа полностью определяется параметрами
графа полностью определяется параметрами  ,
,  вершин, непосредственно доминирующих вершину
вершин, непосредственно доминирующих вершину  .
.
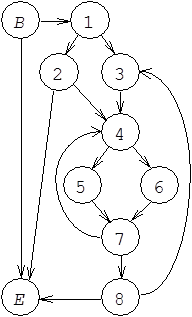
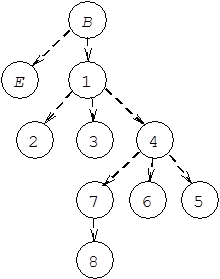
а) б)

в)
Рис. 3.1. Различные формы потоковых графов
Вершина  доминирует вершину
доминирует вершину  тогда и только тогда, когда все пути от начальной вершины В к вершине
тогда и только тогда, когда все пути от начальной вершины В к вершине  проходят через вершину
проходят через вершину  . Отношение доминирования является рефлексивным и транзитивным. Оно может быть представлено деревом доминирования, или D-деревом. На рис. 3.1, б показано D-дерево, соответствующее исходному потоковому графу на рис. 3.1, а. Говорят, что вершина
. Отношение доминирования является рефлексивным и транзитивным. Оно может быть представлено деревом доминирования, или D-деревом. На рис. 3.1, б показано D-дерево, соответствующее исходному потоковому графу на рис. 3.1, а. Говорят, что вершина  непосредственно доминирует вершину
непосредственно доминирует вершину  , если в D-дереве существует дуга
, если в D-дереве существует дуга  . Так, вершина В непосредственно доминирует вершины Е и 1, вершина 1 непосредственно доминирует вершины 2, 3, 4 и т.д. (см. рис. 3.1, б). Формой, занимающей промежуточное положение между потоковым графом и D-деревом, является DJ-граф (рис. 3.1, в). По сути, это D-дерево, дополненное J-дугами, которые вводятся между парой вершин D-дерева, если ни одна из них непосредственно не доминирует другую. Так, на рис. 3.1, в J-дугами являются дуги (2, Е), (2, 4), (8, Е) и т.д.
. Так, вершина В непосредственно доминирует вершины Е и 1, вершина 1 непосредственно доминирует вершины 2, 3, 4 и т.д. (см. рис. 3.1, б). Формой, занимающей промежуточное положение между потоковым графом и D-деревом, является DJ-граф (рис. 3.1, в). По сути, это D-дерево, дополненное J-дугами, которые вводятся между парой вершин D-дерева, если ни одна из них непосредственно не доминирует другую. Так, на рис. 3.1, в J-дугами являются дуги (2, Е), (2, 4), (8, Е) и т.д.
Основные этапы исчерпывающего анализа состоят в следующем:
1) преобразование по определенным правилам DJ-графа в D-дерево;
2) упрощение, на основе исключения переменных, системы потоковых уравнений, записанной для исходного потокового графа;
3) "распространение" решений потоковых уравнений от корня D-дерева к остальным вершинам.
После первого и второго этапов анализа информация на выходе любой вершины определяется через выходную информацию вершин, которые непосредственно доминируют рассматриваемую вершину. Поясним это на примере.
Исходная система потоковых уравнений для графа на рис. 3.1, а имеет следующий вид:
 ,
,
 ,
,
 ,
,
 ,
,
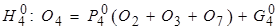 ,
,
 ,
,
 ,
,
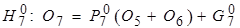 ,
,
 ,
,
 .
.
В этих уравнениях используются символы, смысл которых разъяснен ранее:  – выходная информация,
– выходная информация, 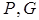 – параметры сохранения и генерации информации. После исключения переменных исходные потоковые уравнения трансформируются следующим образом:
– параметры сохранения и генерации информации. После исключения переменных исходные потоковые уравнения трансформируются следующим образом:
 ,
,
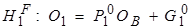 ,
,
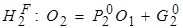 ,
,

 ,
,
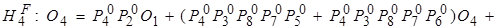

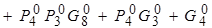 и т.д.
и т.д.
Заметим, что уравнения  и
и  зависимы, причем уравнение
зависимы, причем уравнение  является рекурсивным. Это объясняется циклами в программе, граф которой показан на рис. 3.1, а. Наличие дуги (7, 4) при том, что вершина 4 непосредственно доминирует вершину 7, обуславливает рекурсивность уравнения
является рекурсивным. Это объясняется циклами в программе, граф которой показан на рис. 3.1, а. Наличие дуги (7, 4) при том, что вершина 4 непосредственно доминирует вершину 7, обуславливает рекурсивность уравнения  . Наличие дуги (8, 3) при том, что вершина 7 непосредственно доминирует вершину 8, приводит к зависимости уравнения
. Наличие дуги (8, 3) при том, что вершина 7 непосредственно доминирует вершину 8, приводит к зависимости уравнения  от уравнения
от уравнения  . После выполнения операции замыкания этих двух уравнений результирующие уравнения для вершин 3 и 4 в качестве переменной должны содержать информацию на выходе вершины 1, которая непосредственно доминирует вершины 3, 4 (см. рис. 3.1, б). После замыкания уравнения
. После выполнения операции замыкания этих двух уравнений результирующие уравнения для вершин 3 и 4 в качестве переменной должны содержать информацию на выходе вершины 1, которая непосредственно доминирует вершины 3, 4 (см. рис. 3.1, б). После замыкания уравнения  можно записать уравнение
можно записать уравнение 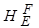 для конечной вершины
для конечной вершины  , которое будет содержать одну переменную
, которое будет содержать одну переменную  .
.
Параметр  является решением уравнения
является решением уравнения  . Вершина В не имеет предшественников, информация на ее выходе генерируется самой вершиной В и является входной информацией для вершин 1 и Е. Решением уравнения
. Вершина В не имеет предшественников, информация на ее выходе генерируется самой вершиной В и является входной информацией для вершин 1 и Е. Решением уравнения 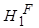 является комбинация параметров
является комбинация параметров 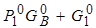 . Это решение "распространяется" по D-дереву к вершинам 2, 3, 4 и т.д.
. Это решение "распространяется" по D-дереву к вершинам 2, 3, 4 и т.д.
Задача инкрементального (incremental) анализа формулируется следующим образом. Пусть для заданной программы получено корректное решение системы потоковых уравнений, например, методом исчерпывающего анализа. Выделим изменяемые части (параметры) этого решения, отражающие соответствующие изменения в программе, в частности, введение или удаление связей по управлению или данным, представленных дугами потокового графа. Требуется после частичных (инкрементальных) изменений параметров решения получить новое решение соответствующей системы потоковых уравнений, не производя для нее полного "пересчета". Это и определяет суть анализа как инкрементального: обновляются лишь те решения, на которые воздействуют частичные модификации потокового графа либо параметров какого-либо исходного уравнения  для некоторой вершины
для некоторой вершины  . Например, результирующее уравнение для вершины 7 потокового графа на рис. 3.1, а после второго этапа исчерпывающего анализа приобретает следующий вид:
. Например, результирующее уравнение для вершины 7 потокового графа на рис. 3.1, а после второго этапа исчерпывающего анализа приобретает следующий вид:
 ,
,
где 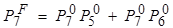 ,
,  .
.
Таким образом, результирующие параметры 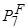 и
и  зависят от исходных параметров
зависят от исходных параметров 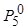 ,
,  и
и  ,
, 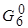 вершин 5 и 6. Следовательно, изменение параметров этих вершин повлияет на параметры вершины 7 и вид решения потокового уравнения. Соответственно, изменяются и решения других уравнений, куда входят параметры
вершин 5 и 6. Следовательно, изменение параметров этих вершин повлияет на параметры вершины 7 и вид решения потокового уравнения. Соответственно, изменяются и решения других уравнений, куда входят параметры 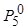 ,
,  ,
,  ,
, 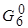 . Однако при этом не нужно воспроизводить всю процедуру решения исходной системы уравнений, чтобы эти изменения учесть.
. Однако при этом не нужно воспроизводить всю процедуру решения исходной системы уравнений, чтобы эти изменения учесть.
До сих пор мы предполагали, что дуги потокового графа являются однотипными и представляют либо передачу управления, либо передачу операндов и т.п. В так называемом 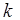 -кратном окружении для анализа потоковый граф программы может содержать
-кратном окружении для анализа потоковый граф программы может содержать 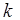 типов дуг. На рис. 3.2 приведен пример такого графа.
типов дуг. На рис. 3.2 приведен пример такого графа.


Рис. 3.2 Потоковый граф с тремя типами дуг для анализа в 3-кратном окружении
Этот граф представляет программу из двух задач (линейных участков, состоящих из операторов 1,...,4 и 5,...,8), которые могут выполняться параллельно. Дуги управления упорядочивают выполнение операторов каждой задачи. Частичный порядок выполнения операторов программы устанавливается с помощью дуг синхронизации, которые вводятся между вершинами, соответствующими P- и V-операциям над бинарными семафорами s1 и s2 (на рис. 3.2 – вершины 2, 5 и 8, 3).
Напомним, для решения проблемы взаимного исключения критических интервалов Дийкстра предложил специальные переменные, называемые семафорами, и две операции P и V над ними. Семафор s принимает целые неотрицательные значения, в частности, может быть бинарным. Операция V присваивает s значение s+1. Если s¹0, то операция P уменьшает s на единицу и процесс продолжается, если s=0, то P не изменяет значения s до тех пор, пока другой процесс не увеличит значение s с помощью операции V. Если один из процессов начинает выполнять P или V-операцию над семафором, то другой процесс не может изменить значение этого семафора до тех пор, пока первый процесс не завершит P или V-операцию либо не будет приостановлен при попытке выполнить P-операцию над семафором s=0. Таким образом, семафоры позволяют синхронизировать действия параллельных процессов.
Так, при выполнении программы, граф которой показан на рис. 3.2, благодаря синхронизации, оператор 2 всегда начинает выполняться раньше оператора 6, а оператор 8 – раньше оператора 4. Кроме этого, в графе на рис. 3.2 показаны транзитивные дуги между вершинами, обозначающими операторы 2, 6 и 8, 4. С помощью этих дуг обеспечивается завершение выполнения тех операторов, которым предшествуют P- и V-операции над семафорами. Оператор 2 устанавливает семафор s1, но не может непосредственно обусловить завершение выполнения оператора 6. Поэтому вводится специальная дуга (2, 6). По аналогии дуга (8, 4) символизирует завершение выполнения оператора 4 после изменения значения семафора s2 V-операцией (оператором 8). Таким образом, граф программы на рис. 3.2 содержит дуги трех типов. Следовательно, для каждой его вершины может существовать три типа источников входной информации, являющейся передачей управления, синхронизацией или завершением выполнения. Это приводит к необходимости введения 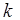 -кратного окружения для анализа (в данном случае
-кратного окружения для анализа (в данном случае 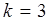 ). В таком окружении можно ставить и решать ряд задач анализа графов параллельных программ , когда результат выполнения какого-либо оператора зависит от типа входной информации. В окружение для анализа вводится множество
). В таком окружении можно ставить и решать ряд задач анализа графов параллельных программ , когда результат выполнения какого-либо оператора зависит от типа входной информации. В окружение для анализа вводится множество 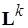 семантических свойств, состоящее из
семантических свойств, состоящее из 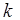 -наборов элементов множества
-наборов элементов множества  . Решение задачи анализа является, как правило, неподвижной точкой
. Решение задачи анализа является, как правило, неподвижной точкой 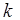 -кратного окружения.
-кратного окружения.
Постановка задачи разметки М-сетей. Рассмотрев некоторые общие подходы к анализу потоковых графов программ, конкретизируем методы анализа с учетом особенностей распределенных вычислений, характерных для масштабируемых систем. М-сеть как специальный вид потокового графа  (см. п. 2.3 раздела 2) соответствует модели распределенных вычислений, в которой процессы взаимодействуют посредством асинхронного обмена сообщениями через буферы. Как уже говорилось, процессы могут иметь как входные, так и выходные, либо только входные буферы. Семантически обе модели эквивалентны. Проблема блокировки, или реализуемости потоковых моделей заключается в согласовании параметров буферов (очередей сообщений) таким образом, чтобы учесть все допустимые истории процессов программы, когда ни один из них не блокируется из-за отсутствия входных сообщений. Исследование реализуемости вычислений может быть сведено к процедуре разметки М-сети. Напомним, маркировка входных и выходных позиций вершин М-сети соответствует ширине буфера (см. рис. 2.6 и 2.7), а метки дуг позволяют получить число сообщений, или глубину буфера, гарантирующую отсутствие "зависаний" программы при любых допустимых историях процессов. Стационарную разметку будем называть неизбыточной, если метки дуг и вершин являются наименьшими из возможных.
(см. п. 2.3 раздела 2) соответствует модели распределенных вычислений, в которой процессы взаимодействуют посредством асинхронного обмена сообщениями через буферы. Как уже говорилось, процессы могут иметь как входные, так и выходные, либо только входные буферы. Семантически обе модели эквивалентны. Проблема блокировки, или реализуемости потоковых моделей заключается в согласовании параметров буферов (очередей сообщений) таким образом, чтобы учесть все допустимые истории процессов программы, когда ни один из них не блокируется из-за отсутствия входных сообщений. Исследование реализуемости вычислений может быть сведено к процедуре разметки М-сети. Напомним, маркировка входных и выходных позиций вершин М-сети соответствует ширине буфера (см. рис. 2.6 и 2.7), а метки дуг позволяют получить число сообщений, или глубину буфера, гарантирующую отсутствие "зависаний" программы при любых допустимых историях процессов. Стационарную разметку будем называть неизбыточной, если метки дуг и вершин являются наименьшими из возможных.
Пусть  – подмножество информационных дуг множества
– подмножество информационных дуг множества  дуг М-сети, инцидентных вершине
дуг М-сети, инцидентных вершине  М-сети,
М-сети,  ,
,  – соответственно входящая и исходящая дуги, или вход и выход, вершины
– соответственно входящая и исходящая дуги, или вход и выход, вершины  . При этом
. При этом  , где
, где  – число операторов программы.
– число операторов программы.
Обозначим через  число аргументов в
число аргументов в  -м буфере – метку входа
-м буфере – метку входа  , инцидентного
, инцидентного  -й входной позиции с маркировкой
-й входной позиции с маркировкой 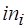 . Глубина
. Глубина  -го буфера входных сообщений процесса, которому соответствует вершина
-го буфера входных сообщений процесса, которому соответствует вершина  , равна
, равна 
 , где
, где  – количество входных буферов.
– количество входных буферов.
Пусть  – число результатов в
– число результатов в  -м выходном буфере (метка выхода
-м выходном буфере (метка выхода  , инцидентного
, инцидентного 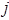 -й выходной позиции вершины
-й выходной позиции вершины  с маркировкой
с маркировкой  ). Тогда глубина
). Тогда глубина 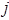 -го выходного буфера равна
-го выходного буфера равна 
 , где
, где  – количество выходных буферов. Наличие альтернатив в развитии вычислений (на рис. 2.6, а это – передача сообщения либо
– количество выходных буферов. Наличие альтернатив в развитии вычислений (на рис. 2.6, а это – передача сообщения либо  , либо
, либо  , а также альтернативная передача управления от
, а также альтернативная передача управления от  ) обуславливает более одной метки дуги. Информационные дуги, инцидентные точке входа в цикл (дуги
) обуславливает более одной метки дуги. Информационные дуги, инцидентные точке входа в цикл (дуги  на рис. 2.6, а), размечаются после эквивалентного преобразования М-сети, обсуждаемого далее, в этом же подразделе.
на рис. 2.6, а), размечаются после эквивалентного преобразования М-сети, обсуждаемого далее, в этом же подразделе.
Рассмотрим два маркированных потоковых графа  и
и 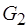 . Пусть
. Пусть  ,
, 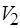 – множества вершин,
– множества вершин, 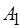 ,
,  – множества дуг графов
– множества дуг графов  ,
, 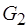 соответственно, а
соответственно, а  – однозначное отображение
– однозначное отображение  в
в 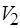 , причем
, причем 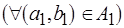
 . Таким образом,
. Таким образом,  – гомоморфизм
– гомоморфизм  в
в 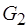 .
.
О п р е д е л е н и е 3.1. Положим,  есть гомоморфизм
есть гомоморфизм  в
в 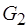 . При этом
. При этом  и
и 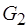 имеют одинаковую маркировку соответствующих дуг
имеют одинаковую маркировку соответствующих дуг  и
и 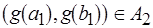 , задаваемую функциями разметки
, задаваемую функциями разметки 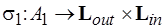 ,
,  . Тогда графы
. Тогда графы  и
и 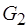 называются равносильными.
называются равносильными.
Пусть  – бесконтурный маркированный потоковый граф с множеством
– бесконтурный маркированный потоковый граф с множеством  вершин и семейством
вершин и семейством  дуг. (Заметим, что
дуг. (Заметим, что  в общем случае является мультиграфом, в котором различным позициям одной и той же вершины соответствуют различные входящие либо исходящие дуги.) Определим порядковую функцию
в общем случае является мультиграфом, в котором различным позициям одной и той же вершины соответствуют различные входящие либо исходящие дуги.) Определим порядковую функцию  ,
,  , графа
, графа  , задающую разбиение множества
, задающую разбиение множества  вершин по
вершин по  уровням. Обозначим через
уровням. Обозначим через  образ вершины
образ вершины 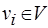 . Ее прообраз обозначим через
. Ее прообраз обозначим через  .
.  и
и  образуют окрестность вершины
образуют окрестность вершины  единичного радиуса.
единичного радиуса.
Уровень есть множество вершин вида
 , где
, где 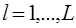 , причем
, причем  , а
, а  . Здесь L – наименьшее целое число такое, что множество прообразов вершин уровня L является пустым.
. Здесь L – наименьшее целое число такое, что множество прообразов вершин уровня L является пустым.
При этом  .
.
Разумеется, можно задать другой порядок уровней:
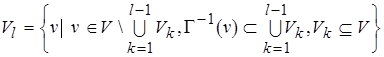 , где
, где  , причем
, причем  , а
, а 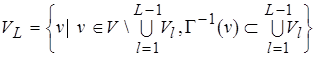 . Будем считать, что при этом определена порядковая функция
. Будем считать, что при этом определена порядковая функция  , обратная
, обратная  .
.
О п р е д е л е н и е 3.2. Бесконтурный маркированный потоковый граф  , где
, где  – множество дуг,
– множество дуг, 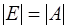 ,
,  – множество дуг равносильного
– множество дуг равносильного  потокового графа
потокового графа  ,
, 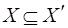 ,
,  ,
,  , с заданной посредством порядковой функции нумерацией уровней
, с заданной посредством порядковой функции нумерацией уровней  , будем называть
, будем называть  -уровневой сетью.
-уровневой сетью.
В графе  , равносильном графу
, равносильном графу  , сохраняется та же маркировка начал и концов дуг, что и в
, сохраняется та же маркировка начал и концов дуг, что и в  , а контуры размыкаются в slt-позициях вершин. Так, М-сети на рис. 2.6, б соответствует трехуровневая сеть, получающаяся при размыкании контура по дуге
, а контуры размыкаются в slt-позициях вершин. Так, М-сети на рис. 2.6, б соответствует трехуровневая сеть, получающаяся при размыкании контура по дуге 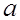 , инцидентной позиции
, инцидентной позиции  (рис. 3.3). Уровни сети – это подмножества вершин
(рис. 3.3). Уровни сети – это подмножества вершин  ,
,  ,
, 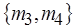 . Исходная М-сеть (см. рис. 2.6, б) и трехуровневая сеть на рис. 3.3 являются равносильными согласно определениям 3.1, 3.2.
. Исходная М-сеть (см. рис. 2.6, б) и трехуровневая сеть на рис. 3.3 являются равносильными согласно определениям 3.1, 3.2.

Рис. 3.3. Трехуровневая сеть
Если уровни нумеруются от выходов ко входам  , то считается заданной прямая порядковая функция
, то считается заданной прямая порядковая функция  , при нумерации от входов к выходам
, при нумерации от входов к выходам  – обратная функция
– обратная функция 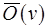 . Понятно, что для любого потокового графа
. Понятно, что для любого потокового графа  существует равносильная ему
существует равносильная ему  -уровневая сеть
-уровневая сеть  . Бесконтурный граф
. Бесконтурный граф  превращается в сеть
превращается в сеть  при задании соответствующей порядковой функции. Положим,
при задании соответствующей порядковой функции. Положим,  содержит контуры. Раскроем все контуры графа
содержит контуры. Раскроем все контуры графа  в
в  -позициях вершин. Вновь полученный бесконтурный граф является гомоморфным образом графа
-позициях вершин. Вновь полученный бесконтурный граф является гомоморфным образом графа  . При сохранении той же маркировки концов дуг, что и в
. При сохранении той же маркировки концов дуг, что и в  , полученный граф по определению 3.1 является равносильным
, полученный граф по определению 3.1 является равносильным  . При задании соответствующей порядковой функции получаем
. При задании соответствующей порядковой функции получаем  -уровневую сеть
-уровневую сеть  , равносильную графу
, равносильную графу  .
.
Теперь поясним, почему равносильное преобразование исходного потокового графа  , в том числе М-сети, в бесконтурную сеть
, в том числе М-сети, в бесконтурную сеть  , является семантически корректным. Рассмотрим М-сеть с циклическим выполнением метаоператора
, является семантически корректным. Рассмотрим М-сеть с циклическим выполнением метаоператора  и теста
и теста  (рис. 3.4, а).
(рис. 3.4, а).

а) в)

б)
Рис. 3.4. Эквивалентные преобразования М-сети
Раскроем цикл, проитерировав  раз пару
раз пару  и сохранив маркировку всех позиций вершин
и сохранив маркировку всех позиций вершин  и
и  , в том числе и метку
, в том числе и метку  входной позиции метаоператора
входной позиции метаоператора  (рис. 3.4, б). Интересующие нас свойства М-сети мы описываем метками дуг и вершин, которые должны быть выявлены в процессе разметки и которые зависят от маркировки входных и выходных позиций вершин (концов и начал дуг). Очевидно, что метки вершин
(рис. 3.4, б). Интересующие нас свойства М-сети мы описываем метками дуг и вершин, которые должны быть выявлены в процессе разметки и которые зависят от маркировки входных и выходных позиций вершин (концов и начал дуг). Очевидно, что метки вершин  ,
,  и соответствующих дуг в
и соответствующих дуг в  -уровневой М-сети на рис. 3.4, б и в двухуровневой М-сети на рис. 3.4, в будут кратными. Поэтому допустимо сведение разметки исходной М-сети (см. рис. 3.4, а) к разметке равносильной ей бесконтурной сети (см. рис. 3.4, в). Из этого примера также должно быть понятным различие между циклическим,
-уровневой М-сети на рис. 3.4, б и в двухуровневой М-сети на рис. 3.4, в будут кратными. Поэтому допустимо сведение разметки исходной М-сети (см. рис. 3.4, а) к разметке равносильной ей бесконтурной сети (см. рис. 3.4, в). Из этого примера также должно быть понятным различие между циклическим,  -кратным выполнением операторов и возможным
-кратным выполнением операторов и возможным  -кратным "участием" некоторого оператора в выполнении программы, где
-кратным "участием" некоторого оператора в выполнении программы, где  – глубина буферов соответствующего процесса, или метка вершины М-сети (см. п. 2.3, рис. 2.11). Итак, разметка любой М-сети может быть сведена к разметке равносильной бесконтурной
– глубина буферов соответствующего процесса, или метка вершины М-сети (см. п. 2.3, рис. 2.11). Итак, разметка любой М-сети может быть сведена к разметке равносильной бесконтурной  -уровневой сети.
-уровневой сети.
Пусть  – частично упорядоченное множество меток дуг (число операндов в буферах), на котором определена операция объединения
– частично упорядоченное множество меток дуг (число операндов в буферах), на котором определена операция объединения 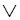 , обладающая свойствами идемпотентности, коммутативности и ассоциативности. Отношение порядка
, обладающая свойствами идемпотентности, коммутативности и ассоциативности. Отношение порядка  таково, что
таково, что 
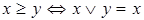 , причем
, причем  . Метки вершин
. Метки вершин  , каждая из которых суть глубина буферов соответствующего процесса, также частичны упорядочены и однозначно определяются свойствами смежных дуг. По аналогии с верхней полуструктурой свойств дуг
, каждая из которых суть глубина буферов соответствующего процесса, также частичны упорядочены и однозначно определяются свойствами смежных дуг. По аналогии с верхней полуструктурой свойств дуг  определяется верхняя полуструктура приведенных свойств вершин
определяется верхняя полуструктура приведенных свойств вершин  .
.
Пара монотонных функций приведения свойств  ,
,  сопоставляет смежным входам либо выходам одно и то же свойство вершины (глубину буферов). Для смежных входов либо выходов определена монотонная функция разметки
сопоставляет смежным входам либо выходам одно и то же свойство вершины (глубину буферов). Для смежных входов либо выходов определена монотонная функция разметки  либо
либо  .
.
Рассмотрим конкретный вид функций приведения и разметки для М-сети. Пусть 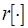 – обозначает наименьшее общее кратное. Если
– обозначает наименьшее общее кратное. Если 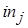 – метка входной позиции, где
– метка входной позиции, где  , которой инцидентен ветвящийся выход метаоператора
, которой инцидентен ветвящийся выход метаоператора  (
(  на рис. 3.3), а
на рис. 3.3), а  – метка его выходной позиции, то все выходы, инцидентные
– метка его выходной позиции, то все выходы, инцидентные 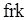 -позиции, имеют метку
-позиции, имеют метку
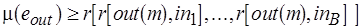 .
.
Функция приведения свойств по выходам – это глубина буферов  процесса, которому соответствует вершина
процесса, которому соответствует вершина  . Эта функция обобщается и на случай, когда у метаоператора больше одной выходной позиции. Для теста эта функция определяется для каждого из альтернативных выходов. Пусть
. Эта функция обобщается и на случай, когда у метаоператора больше одной выходной позиции. Для теста эта функция определяется для каждого из альтернативных выходов. Пусть 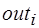 , где
, где  , является меткой выходной позиции вершины
, является меткой выходной позиции вершины  , которой инцидентен вход
, которой инцидентен вход  вершины
вершины  . Глубина буферов процесса, которому соответствует вершина
. Глубина буферов процесса, которому соответствует вершина 
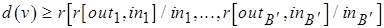 .
.
Метка любого из входов вершины  есть
есть  , а функция приведения свойств по входам –
, а функция приведения свойств по входам –  .
.
Функции разметки по входам и выходам имеют вид:  ,
, 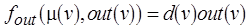 .
.
В М-сети функции приведения определяют глубину буферов, с учетом которой функции разметки "переносят" свойства выходов на входы или наоборот. Это позволяет построить правила разметки, учитывающие свойства всех достижимых из вершины  вершин, а также свойства вершин, из которых достижима вершина
вершин, а также свойства вершин, из которых достижима вершина  . Через приведение свойств дуг учитывается взаимное влияние вершин, находящихся в отношениях прямого или обратного транзитивного замыкания с вершиной
. Через приведение свойств дуг учитывается взаимное влияние вершин, находящихся в отношениях прямого или обратного транзитивного замыкания с вершиной  , но не находящихся в этих отношениях друг с другом, что обеспечивает глобальный анализ сети.
, но не находящихся в этих отношениях друг с другом, что обеспечивает глобальный анализ сети.
Зададим правила замены меток дуг из  и вершины
и вершины  , учитывая, что на верхней полуструктуре свойств
, учитывая, что на верхней полуструктуре свойств  -е применение любого правила разметки приводит к замене метки дуги или вершины
-е применение любого правила разметки приводит к замене метки дуги или вершины 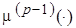 на не меньшую метку
на не меньшую метку  :
:
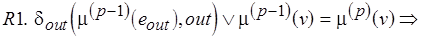
 ,
,
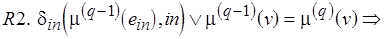
 ,
,
где  ,
, 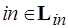 ,
,  ,
, 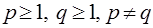 .
.
Стационарной является такая разметка, когда 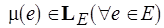 и
и 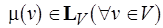 не изменяются никаким применением правил
не изменяются никаким применением правил  ,
,  , причем
, причем
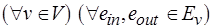
 .
.
Стационарная разметка является неизбыточной, если свойство любых дуги или вершины есть наименьшая верхняя грань множества их допустимых свойств.
Пусть заданы верхние полуструктуры свойств дуг  и вершин
и вершин  , функции приведения и разметки, правила
, функции приведения и разметки, правила  ,
,  замены меток, а также некоторая начальная разметка дуг
замены меток, а также некоторая начальная разметка дуг  и вершин
и вершин 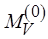 . Задача анализа реализуемости потоковой модели распределенной программы, заданной М-сетью
. Задача анализа реализуемости потоковой модели распределенной программы, заданной М-сетью  , сводится к установлению существования стационарной и нахождению неизбыточной разметки
, сводится к установлению существования стационарной и нахождению неизбыточной разметки  -уровневой сети
-уровневой сети  , равносильной
, равносильной  .
.
Стационарность и неизбыточность разметки. Свойство уровня  ,
, 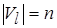 , представим вектором
, представим вектором  , где
, где 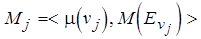 ,
,  ;
; 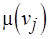 – метка вершины
– метка вершины  , а
, а  – множество меток ее входов и выходов
– множество меток ее входов и выходов  . Разметка сети – это набор свойств уровней
. Разметка сети – это набор свойств уровней  . Начальное свойство уровня обозначим
. Начальное свойство уровня обозначим  , причем
, причем 
 ,
,  .
.
Схемой последовательного анализа свойств сети (ПАСС) назовем определение свойств уровней в соответствии со следующими процедурами:
1) анализ свойств (проход) начинается с уровня, у которого отсутствуют либо преемники, либо предшественники;
2) пусть задана функция  , тогда реализуется первый проход от уровня 1 к уровню
, тогда реализуется первый проход от уровня 1 к уровню  , определение свойств в уровне
, определение свойств в уровне  по правилу
по правилу 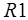 , возвращение к уровню
, возвращение к уровню  от предшественников в уровнях
от предшественников в уровнях  и приведение свойств в
и приведение свойств в  -м уровне по правилу
-м уровне по правилу  ;
;
3) после достижения уровня  реализуется второй проход от предшественников к преемникам, определение свойств в уровне
реализуется второй проход от предшественников к преемникам, определение свойств в уровне  по правилу
по правилу  , возвращение к уровню
, возвращение к уровню  от преемников в уровнях
от преемников в уровнях  и приведение свойств в уровне
и приведение свойств в уровне  по правилу
по правилу 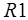 .
.
Шагом ПАСС будем называть определение свойства уровня по правилам 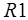 или
или  .
.
Т е о р е м а 3.1. Достигнутая разметка сети  является стационарной тогда и только тогда, когда свойство любого уровня не изменяется после
является стационарной тогда и только тогда, когда свойство любого уровня не изменяется после  шагов ПАСС при любой начальной разметке.
шагов ПАСС при любой начальной разметке.
Д о к а з а т е л ь с т в о. Положим, определена функция  . Пусть достигнутая разметка является стационарной. При первом проходе свойство уровня
. Пусть достигнутая разметка является стационарной. При первом проходе свойство уровня  может измениться однажды в соответствии с правилом
может измениться однажды в соответствии с правилом 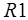 и
и  раз по правилу
раз по правилу  из-за приведения свойств предшественников. При втором проходе свойство уровня
из-за приведения свойств предшественников. При втором проходе свойство уровня  может измениться однажды по правилу
может измениться однажды по правилу  и
и  раз по правилу
раз по правилу 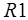 из-за приведения свойств в уровнях
из-за приведения свойств в уровнях  . Следовательно, при любой начальной разметке свойство
. Следовательно, при любой начальной разметке свойство  -го уровня не должно изменяться после (
-го уровня не должно изменяться после ( 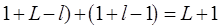 шагов.
шагов.
Докажем, что если после  шага ПАСС свойство какого-либо уровня изменяется, то стационарная разметка вообще не достигается. Пусть реализуется второй проход. Положим, вершина
шага ПАСС свойство какого-либо уровня изменяется, то стационарная разметка вообще не достигается. Пусть реализуется второй проход. Положим, вершина  , где
, где 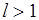 , имеет преемников в уровнях
, имеет преемников в уровнях  . Метку любой из инцидентных ей дуг, полученную при первом проходе, обозначим
. Метку любой из инцидентных ей дуг, полученную при первом проходе, обозначим 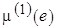 , где
, где  , а после разметки при втором проходе без возвращений к
, а после разметки при втором проходе без возвращений к  -му уровню –
-му уровню – 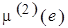 . В силу монотонности функций
. В силу монотонности функций  и
и  при
при  -й разметке уровня
-й разметке уровня  , где
, где  . Положим, что после приведения свойств преемников уровня
. Положим, что после приведения свойств преемников уровня  найдется такая вершина
найдется такая вершина  , что
, что  , где
, где  обозначает переразметку из-за преемников по правилу
обозначает переразметку из-за преемников по правилу  . Зафиксируем
. Зафиксируем  и проведем переразметку уровней с
и проведем переразметку уровней с  -го по
-го по 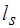 -й по правилу
-й по правилу  . В силу монотонности функций
. В силу монотонности функций  в уровне
в уровне 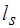 найдется вершина
найдется вершина  такая, что
такая, что 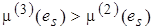 , где
, где 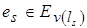 . Тогда, если после возвращения от уровня
. Тогда, если после возвращения от уровня 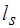 к уровню
к уровню  с применением правила
с применением правила 
 , то процесс разметки никогда не может закончиться. Значит, если после
, то процесс разметки никогда не может закончиться. Значит, если после  шагов при втором проходе с возвращениями свойства уровня
шагов при втором проходе с возвращениями свойства уровня  изменяются, то стационарная разметка не достигается. Поскольку число разметок уровня
изменяются, то стационарная разметка не достигается. Поскольку число разметок уровня  при первом проходе с возвращениями не превышает
при первом проходе с возвращениями не превышает  , то стационарная разметка не достижима, если свойство
, то стационарная разметка не достижима, если свойство  -го уровня изменяется после
-го уровня изменяется после  шагов ПАСС.
шагов ПАСС.
При задании порядковой функции  доказательство теоремы проводится аналогично. Изменяется лишь на противоположную последовательность применения правил
доказательство теоремы проводится аналогично. Изменяется лишь на противоположную последовательность применения правил  . Теорема доказана.
. Теорема доказана.
Таким образом, теорема 3.1 устанавливает критерий стационарности разметки. Стационарной разметки может и не существовать, т.е. потоковая модель является нереализуемой, что означает возможность блокировки вычислений. Соответствующие примеры приводятся в п. 3.2 данного раздела.
Поскольку функции  монотонны, то множество разметок уровня
монотонны, то множество разметок уровня  , достижимых из начальной разметки
, достижимых из начальной разметки  , образует цепь, длина которой конечна, если стационарная разметка существует:
, образует цепь, длина которой конечна, если стационарная разметка существует:
 ,
,
где  .
.
При этом  – верхняя грань этого линейно упорядоченного множества. Пусть
– верхняя грань этого линейно упорядоченного множества. Пусть 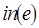 ,
,  – метки входной и выходной позиций, которым инцидентна дуга
– метки входной и выходной позиций, которым инцидентна дуга  М-сети. Если начальная разметка каждого уровня минимальна, т.е.
М-сети. Если начальная разметка каждого уровня минимальна, т.е.  ,
, 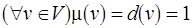 за исключением процессов, не участвующих в альтернативах вычислений, то стационарная разметка М-сети является неизбыточной.
за исключением процессов, не участвующих в альтернативах вычислений, то стационарная разметка М-сети является неизбыточной.
Временную сложность алгоритмов ПАСС определим как функцию от числа шагов разметки уровней. Пусть задана порядковая функция  . Поскольку число шагов разметки уровня
. Поскольку число шагов разметки уровня  при первом проходе составляет
при первом проходе составляет  , то для разметки сети достаточно числа шагов, не превышающего суммы членов арифметической прогрессии
, то для разметки сети достаточно числа шагов, не превышающего суммы членов арифметической прогрессии  . Для разметки сети при втором проходе это – та же величина, поскольку для разметки
. Для разметки сети при втором проходе это – та же величина, поскольку для разметки  -го уровня достаточно
-го уровня достаточно  шагов.
шагов.
Если при повторной переразметке любого из уровней  его свойство строго возрастает, так что
его свойство строго возрастает, так что 
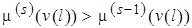 , где
, где 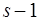 учитывает приведение свойств преемников или предшественников, то стационарной разметки не существует. Таким образом, для установления достижимости стационарной разметки необходимы третий и четвертый проходы. Поэтому общее число шагов разметки не превышает
учитывает приведение свойств преемников или предшественников, то стационарной разметки не существует. Таким образом, для установления достижимости стационарной разметки необходимы третий и четвертый проходы. Поэтому общее число шагов разметки не превышает 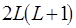 . Следовательно, алгоритмы ПАСС обладают квадратичной асимптотической временной сложностью.
. Следовательно, алгоритмы ПАСС обладают квадратичной асимптотической временной сложностью.
Примеры разметки М-сетей
Разметка элементарных фрагментов. На рис. 3.5 приведены примеры разметки элементарных фрагментов М-сетей по схеме ПАСС: последовательной ветви (рис. 3.5, а), ветвления в  -позиции (рис. 3.5, б), альтернативного слияния в
-позиции (рис. 3.5, б), альтернативного слияния в  -позиции (рис. 3.5, в) и условного ветвления в
-позиции (рис. 3.5, в) и условного ветвления в  -позиции (рис. 3.5, г).
-позиции (рис. 3.5, г).

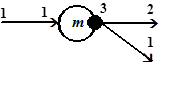



а) б)

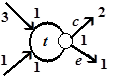



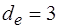
в) г)
Рис. 3.5. Разметка фрагментов М-сети
На рис. 3.5, а под шагом понимается получение метки дуги соответствующего уровня. В значках показаны последовательно получаемые метки дуг, которые кратны числам передаваемых и принимаемых метаоператорами 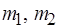 токенов. В итоге на шаге 5 достигаются стационарные и неизбыточные свойства вершин, а именно, значения глубины буферов процессов:
токенов. В итоге на шаге 5 достигаются стационарные и неизбыточные свойства вершин, а именно, значения глубины буферов процессов:  . При разметке ветвления (см. рис. 3.5, б) все дуги, инцидентные
. При разметке ветвления (см. рис. 3.5, б) все дуги, инцидентные 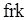 -позиции, получают одну и ту же метку 6. При разметке фрагментов с
-позиции, получают одну и ту же метку 6. При разметке фрагментов с  - и
- и  -позициями (см. рис. 3.5, в и 3.5, г) получаются альтернативные варианты (
-позициями (см. рис. 3.5, в и 3.5, г) получаются альтернативные варианты (  на рис. 3.5, в, г обозначают альтернативные дуги для передачи токенов).
на рис. 3.5, в, г обозначают альтернативные дуги для передачи токенов).
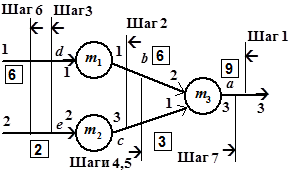
Разметка параллельных ветвей. На рис. 3.6 даны примеры разметки дуг сетей с параллельными ветвями в соответствии со схемой ПАСС. Так же, как и на рис. 3.5, а, шаг ассоциируется с присвоением метки дуге, а в значках приведены стационарные метки дуг.
Разметка является фронтальной, поскольку позволяет получать свойства дуг и вершин в пределах целого уровня. Рассмотрим подробнее процедуру разметки сети на рис. 3.6, а. Исходная маркировка позиций вершин:  ,
,  ,
, 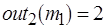 ,
,  ,
, 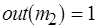 ,
,  ,
, 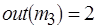 . Обозначим метки начала дуги
. Обозначим метки начала дуги  и концов дуг
и концов дуг  соответственно через
соответственно через  и
и  ,
, 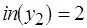 . Начальная разметка дуг отсутствует (символ "-").
. Начальная разметка дуг отсутствует (символ "-").
Шаг 1. Метки дуг  :
:
 ;
;
 .
.
Шаг 2. Метки дуг  :
:
 ;
;
 .
.
Шаг 3. Для согласования глубины выходных буферов метаоператора  выполняется процедура приведения по выходам
выполняется процедура приведения по выходам

и переразмечаются дуги  :
:
 ;
;
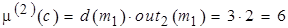 .-метка дуги d!
.-метка дуги d!


а)

б)


в)
Рис. 3.6. Разметка параллельных ветвей с процедурой приведения
Шаг 4. Переразмечаются выходы преемников  :
:
 ;
;
 .
.
Шаг 5. Метка дуги  :
:

 .
.
Далее осуществляется переразметка дуг от входов к выходам сети.
Шаг 6.  ;
;
 .
.
Шаг 7. 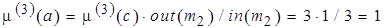 ;
;
 .
.
В общем случае при проходе от входов к выходам сети метки дуг могут изменяться (см. рис. 3.6, б). Для согласования глубины входных буферов метаоператора  на рис. 3.6, б выполняется процедура приведения по входам на шаге 5, переразмечаются входы предшественников
на рис. 3.6, б выполняется процедура приведения по входам на шаге 5, переразмечаются входы предшественников  (шаг 6). Заметим, что процедура приведения по входам может быть выполнена и сразу после шага 2 (см. рис. 3.6, в). Тогда на шаге 4 необходимо переразметить дугу а. Несмотря на такую перестановку шагов, достигается та же стационарная разметка, что и для случая, показанного на рис. 3.6, б. Таким образом, возможны различные варианты (алгоритмы) реализации схемы ПАСС, учитывающие особенности структуры сети, но стационарная и неизбыточная разметка единственна. Значения глубины буферов, соответствующие стационарной разметке в рассмотренных примерах:
(шаг 6). Заметим, что процедура приведения по входам может быть выполнена и сразу после шага 2 (см. рис. 3.6, в). Тогда на шаге 4 необходимо переразметить дугу а. Несмотря на такую перестановку шагов, достигается та же стационарная разметка, что и для случая, показанного на рис. 3.6, б. Таким образом, возможны различные варианты (алгоритмы) реализации схемы ПАСС, учитывающие особенности структуры сети, но стационарная и неизбыточная разметка единственна. Значения глубины буферов, соответствующие стационарной разметке в рассмотренных примерах:  ,
, 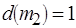 ,
, 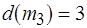 (рис. 3.6, а);
(рис. 3.6, а);  ,
, 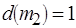 ,
, 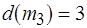 (рис. 3.6, б, в).
(рис. 3.6, б, в).
Альтернативные разметки. Наличие альтернатив в вычислениях приводит к различным разметкам М-сети. Альтернативы в М-сетях реализуются с помощью  - и
- и  -позиций вершин, причем последние ассоциируются только с тестами. Точкой входа в цикл является
-позиций вершин, причем последние ассоциируются только с тестами. Точкой входа в цикл является  -позиция (на рис. 2.6, б и 3.3 это – позиция
-позиция (на рис. 2.6, б и 3.3 это – позиция  ).
).

Рис. 3.3. Трехуровневая сеть
Напомним, семантика  -позиций для организации циклов и альтернативного выбора в развитии вычислений различна. Альтернативные выбор
-позиций для организации циклов и альтернативного выбора в развитии вычислений различна. Альтернативные выбор  и переключение
и переключение  являются аналогом булевой функции исключающее ИЛИ. Смысл введения
являются аналогом булевой функции исключающее ИЛИ. Смысл введения  -позиции для организации циклов иной: соответствующий процесс может быть инициирован данными, передаваемыми по обоим альтернативным входам. Таким образом, здесь имеет место аналог булевой функции ИЛИ. Это и объясняет допустимость эквивалентного преобразования М-сети с циклами путем перехода к равносильной ей бесконтурной
-позиции для организации циклов иной: соответствующий процесс может быть инициирован данными, передаваемыми по обоим альтернативным входам. Таким образом, здесь имеет место аналог булевой функции ИЛИ. Это и объясняет допустимость эквивалентного преобразования М-сети с циклами путем перехода к равносильной ей бесконтурной  -уровневой сети, о чем шла речь в п. 3.1. Следовательно, альтернативные разметки М-сети обусловлены в общем случае наличием
-уровневой сети, о чем шла речь в п. 3.1. Следовательно, альтернативные разметки М-сети обусловлены в общем случае наличием  -позиций для альтернативного выбора и
-позиций для альтернативного выбора и  -позиций для альтернативного переключения потоков данных. Так, существует четыре различных разметки М-сети, показанной на рис. 3.3. Результаты даны в табл. 3.1.
-позиций для альтернативного переключения потоков данных. Так, существует четыре различных разметки М-сети, показанной на рис. 3.3. Результаты даны в табл. 3.1.
Табл. 3.1
Примеры альтернативных разметок М-сети
| Альтернатива | Глубина буферов | ||||
| вычислений | 
| 
| 
| 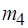
| 
|
 '1' '1'
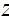 '1' '1'
 '0' '0'
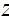 '0' '0'
| 2 4 1 4 | 6 12 3 12 | 3 6 - - | - - 3 12 | 6 12 3 12 |
Альтернативы развития процессов обозначены комбинацией соответствующих дуг для передачи токенов 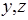 , '1', '0'. Символ "-" в табл. 3.1 означает, что процессы, которым соответствуют метаоператоры
, '1', '0'. Символ "-" в табл. 3.1 означает, что процессы, которым соответствуют метаоператоры  ,
, 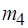 , не участвуют в соответствующей альтернативе вычислений.
, не участвуют в соответствующей альтернативе вычислений.
Рассмотрим более подробно процедуры получения двух альтернативных разметок  '1' и
'1' и 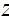 '0' по схеме ПАСС для М-сети на рис. 3.3. Будем считать, что задана прямая порядковая функция, т.е. уровни нумеруются от выходов ко входам сети. В табл. 3.2 и 3.3 приведены значения глубины буферов соответствующих процессов, последовательно получаемые на шагах ПАСС. Для процессов, участвующих в вычислениях, начальная глубина буферов полагается равной 1.
'0' по схеме ПАСС для М-сети на рис. 3.3. Будем считать, что задана прямая порядковая функция, т.е. уровни нумеруются от выходов ко входам сети. В табл. 3.2 и 3.3 приведены значения глубины буферов соответствующих процессов, последовательно получаемые на шагах ПАСС. Для процессов, участвующих в вычислениях, начальная глубина буферов полагается равной 1.
Табл. 3.2
Пошаговая разметка для альтернативы  '1'
'1'
| Шаг | Уровень | Глубина буферов | ||||
| ПАСС | М-сети | 
| 
| 
| 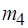
| 
|
| 1 2 3 4 5 6 7 8 | 1 2 1 3 3 2 3 1 | 1 1 1 2 2 2 2 2 | 1 1 1 2 2 2 6 6 | 1 1 3 3 3 3 3 3 | - - - - - - - - | 1 2 2 2 2 6 6 6 |
Табл. 3.3
Пошаговая разметка для альтернативы 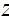 '0'
'0'
| Шаг | Уровень | Глубина буферов | ||||
| ПАСС | М-сети | 
| 
| 
| 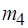
| 
|
| 1 2 3 4 5 6 7 8 | 1 2 1 3 3 2 3 1 | 1 1 1 2 2 2 4 4 | 1 1 1 1 4 4 12 12 | - - - - - - - - | 1 1 1 1 1 1 1 12 | 1 1 1 1 1 12 12 12 |
Шаги ПАСС 1-4 (см. табл. 3.2. и 3.3) представляют процедуру первого прохода от уровня 1 к уровню 3 с применением правила 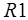 , когда глубина буферов определяется по меткам исходящих дуг. На шаге 3 осуществляется возврат от уровня 2 (теста
, когда глубина буферов определяется по меткам исходящих дуг. На шаге 3 осуществляется возврат от уровня 2 (теста  ) к уровню 1 и производится приведение свойств в соответствии с правилом
) к уровню 1 и производится приведение свойств в соответствии с правилом  по входам метаоператора
по входам метаоператора  (см. табл. 3.2) или метаоператора
(см. табл. 3.2) или метаоператора 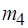 (см. табл. 3.3). Процедура первого прохода завершается на шаге 4 разметкой уровня 3 – определением глубины буферов
(см. табл. 3.3). Процедура первого прохода завершается на шаге 4 разметкой уровня 3 – определением глубины буферов  и
и  по меткам их выходов.
по меткам их выходов.
С шага 5 начинается процедура второго прохода от уровня 3 к уровню 1 с применением правила  , т.е. приведение свойств вершин реализуется по входам. На шаге 5 определяется глубина буферов метаоператоров
, т.е. приведение свойств вершин реализуется по входам. На шаге 5 определяется глубина буферов метаоператоров  ,
,  , причем в альтернативе
, причем в альтернативе 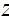 '0' (см. табл. 3.3) свойства
'0' (см. табл. 3.3) свойства  изменяются. На шаге 6 выполняется приведение свойств по входам
изменяются. На шаге 6 выполняется приведение свойств по входам  и затем происходит возвращение у ровню 3 с приведением свойств
и затем происходит возвращение у ровню 3 с приведением свойств  ,
,  по правилу
по правилу 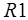 . Наконец, на шаге 8 определяются свойства уровня 1 и на этом процедура разметки заканчивается.
. Наконец, на шаге 8 определяются свойства уровня 1 и на этом процедура разметки заканчивается.
Легко убедиться, что полученные альтернативные разметки являются стационарными и неизбыточными. Таким образом, применение схемы ПАСС сводится к возвратно-поступательным проходам по уровням М-сети и определению их свойств по соответствующим правилам. Практически алгоритмы разметки могут быть реализованы "экономичнее", чем формальная схема. Действительно, если после приведения свойств по входам или выходам вершины ее метка не изменяется, как в случае разметки  '0' на шаге 2 (см. табл. 3.3), то нет необходимости возвращаться к предшественникам или преемникам (например, на шаге 3), поскольку их свойства измениться также не могут. В общем же случае необходимо выполнять все возвраты к уровням предшественников или преемников как, например, при разметке
'0' на шаге 2 (см. табл. 3.3), то нет необходимости возвращаться к предшественникам или преемникам (например, на шаге 3), поскольку их свойства измениться также не могут. В общем же случае необходимо выполнять все возвраты к уровням предшественников или преемников как, например, при разметке  '1' (см. табл. 3.2).
'1' (см. табл. 3.2).
Недостижимость стационарной разметки. В вышерассмотренных примерах стационарная разметка достижима, т.е. соответствующие модели являются реализуемыми и невозможны блокировки вычислений. Теперь рассмотрим примеры противоположной ситуации, когда несмотря на отсутствие ориентированных циклов в М-сетях, блокировка вычислений может возникать. Заметим, что возникновение дедлоков, как правило, связывается с наличием контуров в соответствующих графовых моделях обработки. Примером такой модели может служить граф, вершины которого представляют ресурсные семафоры, а дуги соответствуют последовательности выполнения операций над семафорами (см. п. 3.1). Наличие контура в таком графе свидетельствует о возможности возникновения дедлока. Однако блокировки вычислений могут быть обусловлены и другими причинами, например, взаимозависимостью параллельных путей передачи данных от одного процесса-производителя. Этот эффект был замечен при изучении некоторых акторных моделей, в частности SDF. Пример такого несогласованного SDF-графа рассматривается в п. 2.3 раздела 2 и приведен на рис. 2.5, в.
Рассмотрим бесконтурные М-сети, показанные на рис. 3.7, а, б.
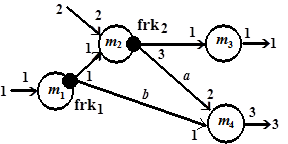

а) б)
Рис. 3.7. Примеры гамаков в М-сетях
Легко убедиться, что стационарной разметки для этих М-сетей не существует. Действительно, в примере на рис. 3.7, а при втором проходе по схеме ПАСС (от  к
к  и далее к
и далее к  ,
,  ) необходимо выполнить приведение по входам метаоператора
) необходимо выполнить приведение по входам метаоператора  . Дуги
. Дуги 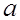 ,
,  до приведения имеют метки
до приведения имеют метки  и
и  . После процедуры приведения их метки приобретают значения
. После процедуры приведения их метки приобретают значения
 ,
,
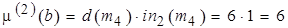 ,
,
где 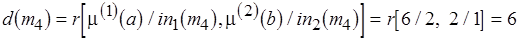 ,
, 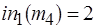 ,
,  .
.
Тогда дуги, исходящие из позиции  метаоператора
метаоператора  (одна из них – дуга
(одна из них – дуга  ) получают общую метку 12. Следовательно, дуга
) получают общую метку 12. Следовательно, дуга 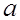 должна получить новую метку 36. Снова необходимо приведение свойств по входам
должна получить новую метку 36. Снова необходимо приведение свойств по входам 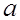 ,
,  вершины
вершины 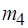 . Понятно, что процедура разметки никогда не может закончиться, т.е. стационарная разметка недостижима. Причина заключается во взаимозависимости разметки путей (
. Понятно, что процедура разметки никогда не может закончиться, т.е. стационарная разметка недостижима. Причина заключается во взаимозависимости разметки путей (  ,
,  ,
, 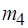 ) и (
) и (  ,
, 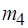 ): результат процесса, которому соответствует метаоператор
): результат процесса, которому соответствует метаоператор  , распространяясь по различным путям, дает аргументы для одного и того же процесса, обозначенного метаоператором
, распространяясь по различным путям, дает аргументы для одного и того же процесса, обозначенного метаоператором 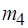 .
.
Так же можно установить, что не достигается стационарная разметка в М-сети на рис. 3.7, б: взаимозависимыми являются процедуры приведения свойств по входам метаоператоров  и
и  . Любое новое приведенное свойство вершины
. Любое новое приведенное свойство вершины  (глубина буферов) требует изменения свойства вершины
(глубина буферов) требует изменения свойства вершины  и наоборот.
и наоборот.
Подграфы М-сетей, подобные приведенным на рис. 3.7, будем называть гамаками. Вершину, соответствующую процессу-производителю, назовем входом (  на рис. 3.7, а), а вершину, обозначающую процесс-потребитель, выходом гамака (
на рис. 3.7, а), а вершину, обозначающую процесс-потребитель, выходом гамака ( 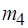 на рис. 3.7, а). Гамак с одним входом и выходом является простейшим. Пример простейшего гамака приведен на рис. 3.7, а. Гамак может быть и составным, когда при одном входе имеется несколько выходов. При этом, разумеется, предполагается, что для каждого из выходов имеется, по крайней мере, два различных пути от входа. М-сеть, показанную на рис. 3.7, б, будем называть связанным гамаком: позиции
на рис. 3.7, а). Гамак с одним входом и выходом является простейшим. Пример простейшего гамака приведен на рис. 3.7, а. Гамак может быть и составным, когда при одном входе имеется несколько выходов. При этом, разумеется, предполагается, что для каждого из выходов имеется, по крайней мере, два различных пути от входа. М-сеть, показанную на рис. 3.7, б, будем называть связанным гамаком: позиции  ,
, 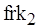 и вершины
и вершины  ,
,  представляют соответственно связанные входы и выходы. Связанный гамак может, конечно же, содержать и более двух входов и выходов. В общем случае могут встречаться подграфы М-сети, представляющие собой сочетания простейших, составных и связанных гамаков.
представляют соответственно связанные входы и выходы. Связанный гамак может, конечно же, содержать и более двух входов и выходов. В общем случае могут встречаться подграфы М-сети, представляющие собой сочетания простейших, составных и связанных гамаков.
Таким образом, наличие гамаков может препятствовать достижимости стационарной разметки и, соответственно, реализуемости соответствующих моделей вычислений. Однако это вовсе не означает, что гамаки всегда приводят к блокировке вычислений. Так, М-сеть на рис. 3.3 содержит два гамака, образованных соответственно вершинами  ,
,  ,
,  и
и  ,
,  ,
, 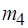 , а также инцидентными им дугами. Тем не менее стационарная разметка достижима для любой из четырех альтернатив развития процессов (см. табл. 3.1). Каким образом, можно установить возможность блокировки вычислений из-за наличия гамаков? В п. 3.1 уже отмечалось, что достаточно повторной переразметки любого из уровней М-сети, чтобы убедиться в достижимости стационарной разметки. Если его свойство при переразметке строго возрастает, то стационарной разметки не существует. Поэтому можно построить конструктивный прием, который следует использовать для проверки существования стационарной разметки М-сети с гамаками.
, а также инцидентными им дугами. Тем не менее стационарная разметка достижима для любой из четырех альтернатив развития процессов (см. табл. 3.1). Каким образом, можно установить возможность блокировки вычислений из-за наличия гамаков? В п. 3.1 уже отмечалось, что достаточно повторной переразметки любого из уровней М-сети, чтобы убедиться в достижимости стационарной разметки. Если его свойство при переразметке строго возрастает, то стационарной разметки не существует. Поэтому можно построить конструктивный прием, который следует использовать для проверки существования стационарной разметки М-сети с гамаками.
Пусть задана прямая порядковая функция и выполнена процедура приведения по входам для вершин-выходов гамака ( 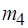 – на рис. 3.7, а). Затем осуществляется разметка дуг гамака обратным фронтом, т.е. по направлению к вершинам-входам гамака (
– на рис. 3.7, а). Затем осуществляется разметка дуг гамака обратным фронтом, т.е. по направлению к вершинам-входам гамака (  – на рис. 3.7, а). Следующий этап – переразметка дуг прямым фронтом от вершин-входов к вершинам-выходам (дуг (
– на рис. 3.7, а). Следующий этап – переразметка дуг прямым фронтом от вершин-входов к вершинам-выходам (дуг (  ,
,  ),
), 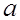 и
и  на рис. 3.7, а). Достаточным признаком того, что гамак не препятствует достижимости разметки, является неизменность меток вершин-выходов, или глубины буферов процессов. Процедура "отражения" обратного (прямого) фронта от входов (выходов) гамака может использоваться в практических алгоритмах обнаружения возможности блокировок вычислений в моделях буферного обмена сообщениями.
на рис. 3.7, а). Достаточным признаком того, что гамак не препятствует достижимости разметки, является неизменность меток вершин-выходов, или глубины буферов процессов. Процедура "отражения" обратного (прямого) фронта от входов (выходов) гамака может использоваться в практических алгоритмах обнаружения возможности блокировок вычислений в моделях буферного обмена сообщениями.


а) б)
Рис. 3.8. Репликация входов гамаков
Другой вопрос, который возникает при наличии гамаков, блокирующих вычисления, заключается в следующем. Каким образом, следует преобразовать М-сеть, чтобы стационарная разметка стала достижимой? Ясно, что для этого каким-то способом нужно устранить взаимозависимость путей, ведущих от входов к выходам гамака. Этого можно добиться за счет репликации, т.е. "тиражирования", вершин-входов или позиций-входов гамаков и инцидентных им дуг. На рис. 3.8, а, б приведены результаты репликации входов гамаков, показанных на рис. 3.7, а и б.
Метаоператор  на рис. 3.7, а заменяется двумя метаоператорами
на рис. 3.7, а заменяется двумя метаоператорами  и
и  , причем соответствующие
, причем соответствующие  ,
,  и
и  процессы должны быть функционально эквивалентными (см. п. 2.1 раздела 2). При этом исчезает позиция
процессы должны быть функционально эквивалентными (см. п. 2.1 раздела 2). При этом исчезает позиция  и устраняется взаимозависимость разметки путей от
и устраняется взаимозависимость разметки путей от  ,
,  к
к 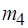 . На рис. 3.8, б показана репликация позиции
. На рис. 3.8, б показана репликация позиции 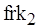 . При этом по дугам
. При этом по дугам 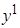 и
и 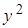 должны передаваться одинаковые данные для метаоператоров
должны передаваться одинаковые данные для метаоператоров  и
и  соответственно. Разумеется, нет необходимости реплицировать входы всех гамаков. Эта процедура применяется лишь к тем гамакам, которые препятствуют достижимости разметки, а для установления этого факта можно использовать "отражение" прямого или обратного фронтов разметки от входов или выходов гамака.
соответственно. Разумеется, нет необходимости реплицировать входы всех гамаков. Эта процедура применяется лишь к тем гамакам, которые препятствуют достижимости разметки, а для установления этого факта можно использовать "отражение" прямого или обратного фронтов разметки от входов или выходов гамака.
Таким образом, основные процедуры алгоритмов разметки М-сетей заключаются в следующем.
1°. Раскрытие циклов, задание порядковой функции, обнаружение гамаков (последнее может быть выполнено построением транзитивного замыкания на графе).
2°. Применение схемы ПАСС.
3°. Переразметка уровней гамака "отражением" фронта.
4°. Если гамак не препятствует достижимости разметки, то к этапу 2°, иначе к этапу 5°.
5°. Репликация входов гамака. К этапу 2°.
Разрешимость задачи анализа потоковых
Дата добавления: 2021-05-18; просмотров: 469; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
