Теоретическая часть для лабораторной работы №3
МАД Лабораторная работа №3
«ИССЛЕДОВАНИЕ МОДЕЛИ ПАРНОЙ ЛИНЕЙНОЙ РЕГРЕССИИ»
Цель работы: построить модели парной и множественной линейной регрессии на основе имеющихся данных, проанализировать качество построенных моделей.
Задание для работы в лаборатории
Требуется построить и исследовать модели парной и множественной линейной регрессии с результативным признаком Y и факторными признаками X1 , X2 , X3, X4 , X5. Исходные данные (лабораторная работа №2) использовать по вариантам. Для выполнения задания воспользоваться методом наименьших квадратов: а) путем решения системы нормальных уравнений, б) путем использования инструмента РЕГРЕССИЯ (Сервис – Анализ данных – РЕГРЕССИОННЫЙ АНАЛИЗ).
1. Формулирование гипотезы о форме связи исследуемого признака и других факторных признаков:
А. Постройте корреляционную матрицу.
Б. Проанализируйте корреляционную матрицу (отберите факторные признаки, наиболее сильно связанные с результативным; выявите мультиколлинеарные факторные признаки).
В. Сделайте предположение о целесообразности построения линейного уравнения регрессии (парного и множественного), включающего наиболее информативные факторные признаки. Запишите модели уравнений регрессии в общем виде.
2. Построение и исследование модели парной линейной регрессии:
А. Рассчитайте параметры парного уравнения регрессии, исходя из выбранных форм связи (линейной).
|
|
|
Б. Поясните интерпретацию уравнения регрессии.
В. Оцените тесноту связи с помощью коэффициента детерминации.
Г. Дайте сравнительную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности.
Д. Оцените качество уравнений регрессии с помощью средней ошибки аппроксимации.
Е. Оцените статистическую значимость результатов регрессионного моделирования с помощью F-критерия Фишера.
Ж. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня.
3. Построение и исследование модели множественной линейной регрессии, включающей все факторные признаки:
А.Рассчитайте параметры линейного уравнения множественной регрессии с перечнем всех факторов (информативных факторов, выявленных в п.1.
Б. Оцените тесноту связи с помощью коэффициента детерминации.
В. Оцените статистическую значимость (существенность) параметров регрессионной модели с помощью t-критерия.
Г. Оцените статистическую значимость уравнения регрессии в целом с помощью F-критерия.
Д. Оцените качество уравнения регрессии через среднюю ошибку аппроксимации.
4. Построение и исследование модели множественной линейной регрессии, включающей только информативные факторные признаки, выявленные в п.1:
|
|
|
А.Рассчитайте параметры линейного уравнения множественной регрессии.
Б. Оцените тесноту связи с помощью коэффициента детерминации.
В. Оцените статистическую значимость (существенность) параметров регрессионной модели с помощью t-критерия.
Г. Оцените статистическую значимость уравнения регрессии в целом с помощью F-критерия.
Д. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
Е. Оцените качество уравнения регрессии через среднюю ошибку аппроксимации.
Ж. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
З. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (α=0,05; α=0,10).
Сравнение полученных в п. 2, 3, 4 результатов (модель парной линейной регрессии и модели множественной линейной регрессии, включающие все факторные признаки и только информативные), используя критерии: коэффициент детерминации, критерий Фишера, критерий Стьюдента, средняя ошибка аппроксимации, сумма квадратов остатков уравнения регрессии. Целесообразно сравнение выполнить в таблице. Оформите выводы.
|
|
|
| Критерий сравнения | Модель парной линейной регрессии | Модель множественной линейной регрессии с включением всех факторов | Модель множественной линейной регрессии с включением только информативных факторов |
| Коэффициент детерминации | |||
| Значение F -критерия и его оценка | |||
| Значения t -критерия и их оценка | |||
| Средняя ошибка аппроксимации | |||
| Сумма квадратов остатков |
Теоретическая часть для лабораторной работы №3
Регрессионный анализ – это статистический метод исследования зависимости случайной величины Y от переменных Х j (j = 1, 2, …, k ), рассматриваемых в регрессионном анализе как неслучайные величины независимо от истинного закона распределения Х j.
Перечислим основные требования, предъявляемые к анализируемой информации:
1) используемые для исследования наблюдения должны являться случайно выбранными из генеральной совокупности объектов. В противном случае исходные данные, представляющие собой определенную выборку из генеральной совокупности, не будут отражать ее характер, полученные по ним выводы о закономерностях развития окажутся бессмысленными и не имеющими никакой практической ценности;
|
|
|
2) требование независимости наблюдений друг от друга.
Зависимость наблюдений друг от друга называется автокорреляцией, для ее устранения в теории корреляционно-регрессионного анализа созданы специальные методы;
3) исходная совокупность данных должна быть однородной, без аномальных наблюдений. Одно-единственное, резко выделяющееся наблюдение может привести к катастрофическим последствиям для регрессионной модели, ее параметры окажутся смещенными, выводы абсурдными;
4) желательно, чтобы исходные данные для анализа подчинялись нормальному закону распределения. Нормальный закон распределения используется для того, чтобы при проверке значимости коэффициентов корреляции и построении для них интервальных границ можно было использовать определенные критерии. Если же проверять значимость и строить интервальные оценки не требуется, переменные могут иметь любой закон распределения.
В регрессионном анализе при построении уравнения регрессии требование нормальности распределения исходных данных предъявляется лишь к результативной переменной Y. Обычно предполагается, что случайная величина Y имеет нормальный закон распределения с условным математическим ожиданием 
Ý = ( x 1 , …, xk ), являющимся функцией от аргументов x j, с постоянной, не зависящей от аргументов дисперсией σ2.
Независимые факторы Х j рассматриваются как неслучайные величины и могут в действительности иметь любой закон распределения. Как и в случае корреляционного анализа, требование нормальности распределения нужно для проверки значимости регрессионного уравнения, его коэффициентов и нахождения доверительных интервалов;
5) число наблюдений, по которым устанавливается взаимосвязь признаков и строится модель регрессии, должно превышать количество факторных признаков хотя бы в 3-4 раза (а лучше в 8-10 раз).
Это объясняется тем, что статистическая связь проявляется только при значительном числе наблюдений на основе действия закона больших чисел, причем, чем связь слабее, тем больше требуется наблюдений для установления связи, чем сильнее - тем меньше;
6) факторные признаки Х j не должны находиться между собой в функциональной зависимости. Значительная связь независимых (факторных, объясняющих) признаков между собой указывает на мультиколлениарность. Ее наличие приводит к построению неустойчивых регрессионных моделей, «ложных» регрессий.
Для проведения регрессионного анализа из (k+1)-мерной генеральной совокупности ( Y , X 1 , X 2 , …, Xj , …, Xk ) берется выборка объемом n и каждое i-ое наблюдение характеризуется значениями переменных (y i , xi 1 , xi 2 , …, xij , …, xik ), где xij - значение j –ой переменной для i-го наблюдения (i = 1,2,…, n ), y i – значение результативного признака для i -го наблюдения.
Наиболее часто используется множественная линейная регрессионная модель. В матричной форме она имеет вид:
, …. ()
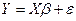где Y – случайный вектор-столбец размерности (n х 1) наблюдаемых значений результативного признака (y1, y2,…, yn);
X – матрица размерности [ n x ( k +1)] наблюдаемых значений аргументов; элемент матрицы xij рассматривается как неслучайная величина (i = 1, 2, …, n , j = 0, 1, 2, …, k);
β – вектор-столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии) модели;
ε – случайный вектор-столбец размерности (n x 1) ошибок наблюдений (остатков). Компоненты вектора ε независимы между собой, имеют нормальный закон распределения с нулевым математическим ожиданием и постоянной дисперсией.
Для оценки вектора β наиболее часто используют метод наименьших квадратов (МНК), согласно которому в качестве оценки принимают вектор b, который минимизирует сумму квадратов отклонения наблюдаемых значений 
от модельных значений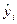 
, т.е. квадратичную форму:
()
Справочные материалы для выполнения лабораторной работы №3 находятся в Приложении Б. Пояснения к результатам использования инструмента РЕГРЕССИЯ (Сервис – Анализ данных – РЕГРЕССИОННЫЙ АНАЛИЗ) сведены в табл. 3.1, 3.2.
Таблица 3.1 - Регрессионная статистика в отчете Excel
| Наименование в отчете Excel | Принятое наименование | Формула |
| Множественный R | Коэффициент множественной корреляции, индекс корреляции | 
|
| R-квадрат | Коэффициент детерминации, R2 |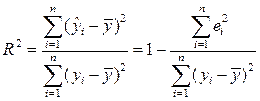 
|
| Нормированный R-квадрат | Скорректированный R2 | 
|
| Стандартная ошибка | Среднеквадратическое отклонение от модели |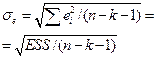 
|
| Наблюдения | Количество значений переменной Y | n |
Множественный R – коэффициент корреляции. Он равен парному линейному коэффициенту корреляции для парного линейного уравнения регрессии. В противном случае его следует рассматривать просто как корень коэффициента детерминации.
R-квадрат – это коэффициент детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
или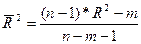 
,
где n – количество значений переменной Y,
m – количество факторных признаков Х j .
Недостатком коэффициента детерминации R-квадрат является то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный, который в отличие от R-квадрат может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Стандартная ошибка - среднее квадратическое отклонение от модели.
Таблица 3.2 - Дисперсионный анализ в отчете Excel
| Наименование в отчете Excel | Df – число степеней свободы | SS – сумма квадратов | MS – дисперсия на одну степень свободы | F- критерий Фишера |
| Регрессия | m |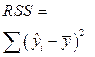 
| 
| 
|
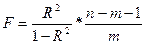
| Остаток | n – m –1 | 
| 
| |
| Итого | n – 1 |
| ||
Приведем некоторые обозначения, используемые в инструменте РЕГРЕССИЯ, для анализа регрессионных уравнений.
Df– число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Значимость F определяется как вероятность полученного значения критериальной статистики. Если эта вероятность меньше, например, 0.05 (заданного уровня значимости), то гипотеза о незначимости регрессии (т.е. гипотеза о том, что все коэффициенты функции регрессии равны нулю) отвергается и считается, что регрессия значима.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
t – значение – расчетное значение статистики Стьюдента 
; используется для оценки значимости коэффициентов уравнения регрессии.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии. Для этого вычисляются уровни значимости, соответствующие значениям критериальных статистик. Если вычисленный уровень значимости меньше заданного уровня значимости (например, 0.05). то принимается гипотеза о значимом отличии коэффициента от нуля; в противном случае принимается гипотеза о незначимом отличии коэффициента от нуля, т.е. что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В столбцах Нижние 95% и Верхние 95% приводятся границы доверительных интервалов с доверительным уровнем 0.95. Эти границы вычисляются по формулам
Нижние 95% = Коэффициент - Стандартная ошибка * tα;
Верхние 95% = Коэффициент + Стандартная ошибка * tα. Здесь tα – квантиль порядка α распределения Стьюдента с (n-m-1) степенью свободы. В данном случае α = 0.95.
Аналогично вычисляются границы доверительных интервалов в столбцах Нижние 90.0% и Верхние 90.0%.
Пример 1.
По семи территориям Уральского района за 2016 г. известны значения двух признаков (табл.3.3).
Таблица 3.3 - Исходные данные
| Район | Расходы на покупку продовольственных товаров в общих расходах, %, у | Среднедневная заработная плата одного работающего, руб., х |
| Удмуртская респ. | 68,8 | 45,1 |
| Свердловская обл. | 61,2 | 59,0 |
| Башкортостан | 59,9 | 57,2 |
| Челябинская обл. | 56,7 | 61,8 |
| Пермская обл. | 55,0 | 58,8 |
| Курганская обл. | 54,3 | 47,2 |
| Оренбургская обл. | 49,3 | 55,2 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры парного линейного уравнения регрессии. Для выполнения задания воспользоваться методом наименьших квадратов.
2. Оценить модель через парный линейный коэффициент корреляции, коэффициент детерминации, среднюю ошибку аппроксимации Ā и F-критерий Фишера.
3. Дать сравнительную оценку силы связи фактора с результатом с помощью среднего коэффициента эластичности.
4. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (α=0,05; α=0,10).
Замечание
Прогнозное значение уп определяется путем подстановки в уравнение регрессии 
соответствующего (прогнозного) значения x п . Вычисляется средняя стандартная ошибка прогноза 
:
; 
.
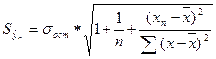Строится доверительный интервал прогноза:
.
Решение
1. Для расчета параметров а и b линейной регрессии у = а + b·х
решаем систему нормальных уравнений относительно а и b:
n·a+b∑x=∑y,
a∑x+b∑x2=∑y·x.
По исходным данным рассчитываем ∑у, ∑x, ∑yx, ∑x2, ∑y2. (табл.2.5)
Таблица 3.4 – Вспомогательная таблица
| y | x | yx | x2 | у2 | ŷх | y-ŷх | Ai | |
| 1 | 68,8 | 45,1 | 3102,88 | 2034,01 | 4733,44 | 61,3 | 7,5 | 10,9 |
| 2 | 61,2 | 59,0 | 3610,80 | 3481,00 | 3745,44 | 56,5 | 4,7 | 7,7 |
| 3 | 59,9 | 57,2 | 3426,28 | 3271,84 | 3588,01 | 57,1 | 2,8 | 4,7 |
| 4 | 56,7 | 61,8 | 3504,06 | 3819,24 | 3214,89 | 55,5 | 1,2 | 2,1 |
| 5 | 55,0 | 58,8 | 3234,00 | 3457,44 | 3025,00 | 56,5 | -1,5 | 2,7 |
| 6 | 54,3 | 47,2 | 2562,96 | 2227,84 | 2948,49 | 60,5 | -6,2 | 11,4 |
| 7 | 49,3 | 55,2 | 2721,36 | 3047,04 | 2430,49 | 57,8 | -8,5 | 17,2 |
| Итого | 405,2 | 384,3 | 22162,34 | 21338,41 | 23685,76 | 405,2 | 0,0 | 56,7 |
| Среднее значение | 57,89 | 54,90 | 3166,05 | 3048,34 | 3383,68 | X | X | 8,1 |
| Σ | 5,74 | 5,86 | X | X | X | X | X | X |
| Σ 2 | 32,92 | 34,34 | X | X | X | X | X | X |
Уравнение регрессии: ŷ = 76,88-0,35 х. С увеличением среднедневной заработной платы на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта.
2. Рассчитаем линейный коэффициент парной корреляции:
|
|
Связь умеренная, обратная.
Определим коэффициент детерминации:
r2xy=(-0,35)2 =0,127.
Вариация результата на 12,7% объясняется вариацией факторов. Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения ух. Найдем величину средней ошибки аппроксимации Ā :
= 
.
В среднем расчетные значения отклоняются от фактических на 8,1%.
Рассчитаем F-критерий:
|
|
Fтабл= 6,61. Fфакт< Fтабл.
Полученное значение указывает на необходимость принять гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.
3. Рассчитаем средний коэффициент эластичности:
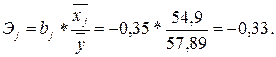
Таким образом, при увеличении среднедневной заработной платы одного работающего (x) на 1% расходы на покупку продовольственных товаров в общих расходах (y) снижаются на 0,33%.
Пример 2.
По данным n=20 сельскохозяйственных районов требуется построить регрессионную модель урожайности на основе следующих показателей: у - урожайность зерновых культур (ц/га); х1 - число колесных тракторов (приведенной мощности) на 100 га; х2 – число зерноуборочных комбайнов на 100 га; х3 – число орудий поверхностной обработки почвы на 100 га; х4 – количество удобрений, расходуемых на гектар; х5 – количество химических средств оздоровления растений, расходуемых на гектар. Исходные данные для анализа приведены в таблице 3.5.
Таблица 3.5 - Исходные данные
| Номер наблюдения | y | Х1 | х2 | х3 | х4 | х5 |
| 1 | 9,70 | 1,59 | 0,26 | 2,05 | 0,32 | 0,14 |
| 2 | 8,40 | 0,34 | 0,28 | 0,46 | 0,59 | 0,66 |
| 3 | 9,00 | 2,53 | 0,31 | 2,46 | 0,30 | 0,31 |
| 4 | 9,90 | 4,63 | 0,40 | 6,44 | 0,43 | 0,59 |
| 5 | 9,60 | 2,16 | 0,26 | 2,16 | 0,39 | 0,16 |
| 6 | 8,60 | 2,16 | 0,30 | 2,69 | 0,32 | 0,17 |
| 7 | 12,50 | 0,68 | 0,29 | 0,73 | 0,42 | 0,23 |
| 8 | 7,60 | 0,35 | 0,26 | 0,42 | 0,21 | 0,08 |
| 9 | 6,90 | 0,52 | 0,24 | 0,49 | 0,20 | 0,08 |
| 10 | 13,50 | 3,42 | 0,30 | 3,02 | 1,37 | 0,73 |
| 11 | 9,70 | 1,78 | 0,30 | 3,19 | 0,73 | 0,17 |
| 12 | 10,70 | 2,40 | 0,32 | 3,30 | 0,25 | 0,14 |
| 13 | 12,10 | 9,36 | 0,40 | 11,51 | 0,39 | 0,38 |
| 14 | 9,70 | 1,72 | 0,28 | 2,26 | 0,82 | 0,17 |
| 15 | 7,00 | 0,59 | 0,29 | 0,60 | 0,13 | 0,35 |
| 16 | 7,20 | 0,28 | 0,26 | 0,30 | 0,09 | 0,15 |
| 17 | 8,20 | 1,64 | 0,29 | 1,44 | 0,20 | 0,08 |
| 18 | 8,40 | 0,09 | 0,22 | 0,05 | 0,43 | 0,20 |
| 19 | 13,10 | 0,08 | 0,25 | 0,03 | 0,73 | 0,20 |
| 20 | 8,70 | 1,36 | 0,26 | 1,17 | 0,99 | 0,42 |
Решение
С целью анализа взаимосвязи показателей построим матрицу парных коэффициентов корреляции (таблица 3.6).
Таблица 3.6 – Матрица парных коэффициентов корреляции
| Y | Х1 | х2 | х3 | х4 | х5 | |
| Y | 1,00 | |||||
| Х1 | 0,43 | 1,00 | ||||
| Х2 | 0,37 | 0,85 | 1,00 | |||
| Х3 | 0,40 | 0,98 | 0,88 | 1,00 | ||
| Х4 | 0,58 | 0,11 | 0,03 | 0,03 | 1,00 | |
| Х5 | 0,33 | 0,34 | 0,46 | 0,28 | 0,57 | 1,00 |
Анализ корреляционной матрицы показывает, что результативный показатель наиболее тесно связан с показателем х4 (количество удобрений, расходуемых на гектар). 
.
В тоже время связь между признаками-факторами достаточно тесная. Например, существует практически функциональная связь между числом колесных тракторов х1 и числом орудий поверхностной обработки почвы х3 ( 
). Это свидетельствует о наличии мультиколлинеарности между признаками х1 и х3. Признаки х1 и х2 , а также х2 и х3 тоже мультиколлинеарны ( 
; 
). Делаем вывод о том, что признаки-факторы, которые мултиколлинеарны, одновременно в уравнение регрессии включены быть не могут.
Продемонстрируем целесообразность такого вывода. Построим регрессионную модель урожайности, включив в нее все исходные показатели.
.
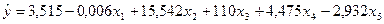Для проверки гипотезы о существенности коэффициентов рассчитаем для каждого коэффициента уравнения регрессии 
: 
; 
; 
; 
; 
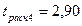. Критическое значение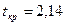 
найдено по таблице t-распределения при уровне значимости α=0,05 и числе степеней свободы ν=14 (ν= 20 – 5 – 1). Из уравнения следует, что статистически существенным является коэффициент регрессии только при х4, так как 
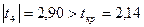. Не поддаются экономической интерпретации отрицательные знаки коэффициентов регрессии при х1 и х5 . Из уравнения следует, что повышение насыщенности сельского хозяйства колесными тракторами х1 и средствами оздоровления растений х5 отрицательно сказывается на урожайности. Таким образом, полученное уравнение регрессии использовать на практике нельзя.
После реализации алгоритма пошагового регрессионного анализа с исключением переменных и учетом того, что в уравнение должна войти только одна из трех тесно связанных переменных (х1,, х2 , х3.), получаем окончательное уравнение регрессии:
.
В уравнение включен х1 , как определяющий из трех показателей. Уравнение значимо при α=0,05, так как 
, найденного по таблице F-распределения при α=0,05;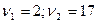 
. Существенны и все коэффициенты регрессии 
и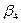 
. В уравнении 
=2,11 (α=0,05; 
). Коэффициент регрессии следует признать существенным ( ≠0) из экономических соображений, при этом 
лишь незначительно меньше =2,11. При α=0,1 =1,76 и статистически существенен. Аналогично существенен и 
: 
.
Интерпретация уравнения регрессии: из уравнения следует, что увеличение на 1 числа тракторов на 100 га пашни приводит к росту урожайности зерновых в среднем на 0,345 ц/га (b1=0,345).
Коэффициенты эластичности Э1=0,068 и Э2=0,161 показывают, что при увеличении показателей х1 и х4 на 1 % урожайность зерновых повышается соответственно на 0,068% и 0,161% ( 
) .
Множественный коэффициент детерминации 
свидетельствует о том, что только 46,9% вариации урожайности объясняется вошедшими в модель показателями (х1 и х4), то есть насыщенностью растениеводства тракторами и удобрениями. Остальная часть вариации обусловлена действием неучтенных факторов (х2 , х3 , х5, погодных условий и др.).
Средняя относительная ошибка аппроксимации 
характеризует адекватность модели.
Дата добавления: 2021-04-24; просмотров: 135; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!