Метод Ньютона (метод касательных)
Численные методы решения нелинейных уравнений
Пусть имеется уравнение вида
f(x)= 0
где f(x) — заданная алгебраическая или трансцендентная функция.
Решить уравнение — значит найти все его корни, то есть те значения x, которые обращают уравнение в тождество.
Если уравнение достаточно сложно, то задача точного определения корней является в некоторых случаях нерешаемой. Поэтому ставится задача найти такое приближенное значение корня xПP, которое отличается от точного значения корня x* на величину, по модулю не превышающую указанной точности (малой положительной величины) ε, то есть
│x* – xпр │< ε
Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.
Этапы приближенного решения нелинейных уравнений
Приближенное решение уравнения состоит из двух этапов:
· Отделение корней, то есть нахождение интервалов из области определения функции f(x), в каждом из которых содержится только один корень уравнения f(x)=0.
· Уточнение корней до заданной точности.
Отделение корней
Отделение корней можно проводить графически и аналитически.
Для того чтобы графически отделить корни уравнения, необходимо построить график функции f(x). Абсциссы точек его пересечения с осью Ox являются действительными корнями уравнения.
Для примера рассмотрим задачу решения уравнения

где угол x задан в градусах. Указанное уравнение можно переписать в виде

Для графического отсечения корней достаточно построить график функции
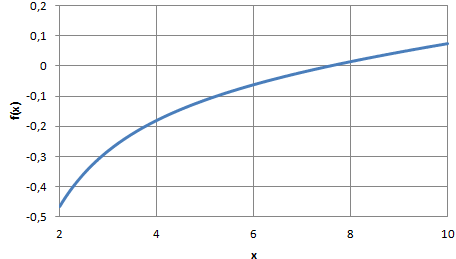
Из рисунка видно, что корень уравнения лежит в промежутке x∈(6;8).
|
|
|
Аналитическое отделение корней
Аналитическое отделение корней основано на следующих теоремах.
Теорема 1. Если непрерывная функция f(x) принимает на концах отрезка [a; b] значения разных знаков, т.е.

то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.
Уточнение корней
Для уточнения корней может использоваться один из следующих методов:
· Метод последовательных приближений (метод итераций)
· Метод Ньютона (метод касательных)
· Метод секущих (метод хорд)
· Метод половинного деления (метод дихотомии)
Метод последовательных приближений (метод итераций)
Метод итерации — численный метод решения математических задач, используемый для приближённого решения алгебраических уравнений и систем. Суть метода заключается в нахождении по приближённому значению величины следующего приближения (являющегося более точным). Метод позволяет получить решение с заданной точностью в виде предела последовательности итераций. Характер сходимости и сам факт сходимости метода зависит от выбора начального приближения решения.
Функциональное уравнение может быть записано в виде
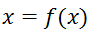
Функцию f(x) называют сжимающим отображением.
|
|
|
Последовательность чисел x0, x1 ,…, xn называется итерационной, если для любого номера n>0 элемент xn выражается через элемент xn-1 по рекуррентной формуле
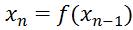
а в качестве x0 взято любое число из области задания функции f(x).
Реализация на C++ для рассмотренного выше примера

Уравнение может быть записано в форме
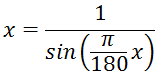
Метод Ньютона (метод касательных)
Если известно начальное приближение x0 корня уравнения f(x)=0, то последовательные приближения находят по формуле
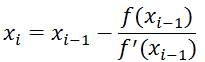
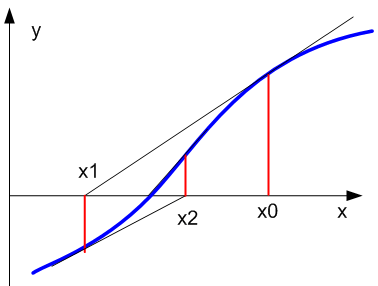
Графическая интерпретация метода касательных имеет вид
Реализация на C++
Для заданного уравнения

производная будет иметь вид 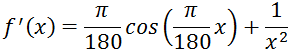
Метод секущих (метод хорд)
Если x0, x1 - приближенные значения корня уравнения f(x) = 0 и выполняется условие

то последующие приближения находят по формуле

Методом хорд называют также метод, при котором один из концов отрезка закреплен, т.е. вычисление приближения корня уравнения f(x) = 0 производят по формулам:

Геометрическая интерпретация метода хорд:
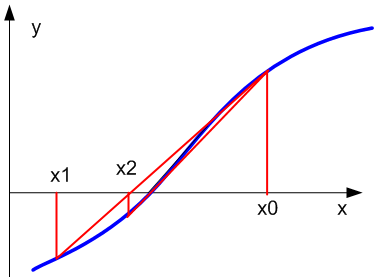
|
|
|
Дата добавления: 2021-04-24; просмотров: 50; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
