Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Алгебра. 9-а класс. 27.05.2020.
Тема урока: Повторение и систематизация курса алгебры 7-9 класса. Решение неравенств и систем неравенств.
Теперь перейдем к решению неравенств и их систем. Основной метод их решения – метод интервалов. Ниже вы можете найти решение более сложного дробно-рационального неравенства. Хотя вся «сложность» заключается лишь в довольно громоздких преобразованиях, а ход решения и алгоритм везде одинаковый.
Решение дробно-рационального неравенства
Пример. Решить неравенство:
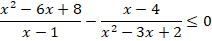
Решение
ОДЗ:
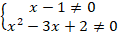
Откуда:
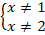
Решаем соответствующее уравнение:

Разложим числитель первой дроби и знаменатель второй дроби на множители:

Домножим числитель и знаменатель первой дроби на  , приведя, таким образом, дроби к общему знаменателю:
, приведя, таким образом, дроби к общему знаменателю:
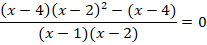
Домножим обе части уравнения на 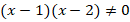 :
:

В полученном уравнении вынесем 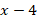 за скобку:
за скобку:

Раскроем квадрат:
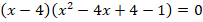
Приведем подобные слагаемые:

Откуда:

Решим первое уравнение:

Решим второе уравнение. По теореме Виета:


Расставляем на оси особые точки ОДЗ и корни уравнения. Методом пробной точки определяем знаки на каждом интервале. Выбираем интервалы с нужным знаком (см. рис. 3).

Рис. 3. Иллюстрация к примеру
Получаем ответ:  .
.
Ответ:  .
.
Задание 2. Решить неравенство:

Решение
Сначала укажем ОДЗ. Подкоренные выражения должны быть неотрицательны. При этом не должно быть деления на ноль, то есть:
|
|
|
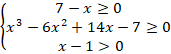
Далее нужно решить само неравенство. Это можно сделать сразу методом интервалов, но этот путь будет достаточно громоздким. Попробуем его немного упростить.
1. Умножим обе части неравенства на положительную величину  :
:

2. Слева и справа стоят неотрицательные величины. При возведении в квадрат обеих частей знак неравенства сохранится. Это верно, поскольку при положительных значениях аргумента функция 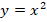 является возрастающей (см. рис. 4).
является возрастающей (см. рис. 4).

Рис. 4. При положительных значениях аргумента функция 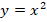 возрастает
возрастает
Большему значению аргумента соответствует большее значение функции:
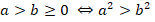
Таким образом, избавляемся от корней в обеих частях неравенства:

Итак, должно выполняться это неравенство и все неравенства из ОДЗ. То есть исходное иррациональное неравенство эквивалентно следующей системе неравенств:

Теперь осталось решить каждое из неравенств методом интервалов и найти пересечение полученных областей. Но есть одна маленькая деталь: решить уравнение  будет проблематично, т. к. оно не имеет целых корней. А мы научились решать кубические уравнения только с целыми корнями. Как же быть?
будет проблематично, т. к. оно не имеет целых корней. А мы научились решать кубические уравнения только с целыми корнями. Как же быть?
Внимательно посмотрим на условия из нашей системы.  , а
, а  . Значит, их произведение
. Значит, их произведение 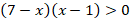 . При этом выражение
. При этом выражение  , а значит, и больше нуля. То есть из первого второго и четвертого неравенств автоматически следует, что выполняется третье неравенство. Значит, условие
, а значит, и больше нуля. То есть из первого второго и четвертого неравенств автоматически следует, что выполняется третье неравенство. Значит, условие  избыточно и нам достаточно решить систему из трех неравенств:
избыточно и нам достаточно решить систему из трех неравенств:
|
|
|

Проще всего решить второе и третье неравенства:


Для решения первого неравенства воспользуемся методом интервалов:
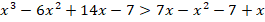
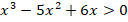
Решаем соответствующее уравнение:

Вынесем  за скобку:
за скобку:


Решая квадратное уравнение, получаем:
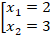
Расставляем корни на оси, методом пробной точки определяем знаки на интервалах, выбираем нужные интервалы (см. рис. 5).

Рис. 5. Иллюстрация к заданию 8
Отметим на оси решения других двух неравенств и найдем их пересечение (см. рис. 6).

Рис. 6. Иллюстрация к заданию 8
Получаем ответ:

Ответ:  .
.
Итак, мы вспомнили основные методы решения неравенств, а также их систем.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-портал fizmat.by (Источник)
2. Интернет-портал yaklass.ru (Источник)
3. Интернет-портал math-prosto.ru (Источник)
Дата добавления: 2021-04-15; просмотров: 47; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
