Однородные дифференциальные уравнения первого порядка
Изучите теоретический материал (часть 1).
Запишите Примеры решения в рабочую тетрадь.
Выполните любые (по вашему выбору) 5 заданий из практической части 1-16.
4. Решенные задания практической части направлять в личном сообщении https://vk.com/veremeenko71
Теоретический материал
ЧАСТЬ 1
Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную 
;
2) зависимую переменную 
(функцию);
3) первую производную функции: 
.
В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная , и не было производных высших порядков – 
, 
и т.д.
Решить дифференциальное уравнение – это значит, найти множество функций 
, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.
Пример 1 
В первую очередь нужно переписать производную немного в другом виде. Вспоминаем громоздкое обозначение производной: 
. Итак, на первом этапе переписываем производную в нужном нам виде: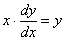 
переменные легко разделяются перекидыванием множителей по правилу пропорции: 
Переменные разделены. В левой части – только «игреки», в правой части – только «иксы».
Следующий этап – интегрирование дифференциального уравнения.
Разумеется, интегралы нужно взять. В данном случае они табличные:
вместо записи обычно пишут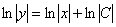 
.
|
|
|
Здесь 
– это такая же полноценная константа, как и 
. Зачем это нужно? А для того, чтобы легче было выразить «игрек». Используем школьное свойство логарифмов: 
. В данном случае: 
Теперь логарифмы и модули можно с чистой совестью убрать с обеих частей:
Функция представлена в явном виде. Это и есть общее решение.
Множество функций 
является общим решением дифференциального уравнения .
Придавая константе различные значения, можно получить бесконечно много частных решений дифференциального уравнения. Любая из функций 
, 
, 
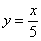и т.д. будет удовлетворять дифференциальному уравнению .
Иногда общее решение называют семейством функций. В данном примере общее решение – это семейство линейных функций, а точнее, семейство прямых пропорциональностей.
Многие дифференциальные уравнения довольно легко проверить. Делается это очень просто, берём найденное решение и находим производную:
Подставляем наше решение и найденную производную 
в исходное уравнение :
– получено верное равенство, значит, решение найдено правильно. Иными словами, общее решение удовлетворяет уравнению .
Пример 2
Найти частное решение дифференциального уравнения 
, удовлетворяющее начальному условию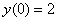 
|
|
|
По условию требуется найти частное решение ДУ, удовлетворяющее начальному условию. Такая постановка вопроса также называется задачей Коши.
Переписываем производную в нужном виде: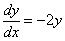 
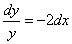Интегрируем уравнение: 
В данном случае:
Константу в показателе обычно спускают. Если подробно, то происходит это так.
Запомните «снос» константы, это второй технический приём, который часто используют в ходе решения дифференциальных уравнений.
Итак, общее решение: 
. На завершающем этапе нужно найти частное решение, удовлетворяющее заданному начальному условию 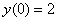. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку:
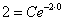
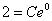
То есть, 
– это и есть нужное нам частное решение.
Пример 3
Решить дифференциальное уравнение 
Решение: Переписываем производную в нужном нам виде: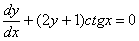 
Переносим второе слагаемое в правую часть со сменой знака: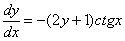 
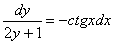Переменные разделены, интегрируем обе части: 
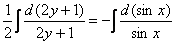
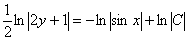Решение распишу очень подробно: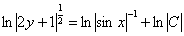 
Упаковка завершена, убираем логарифмы: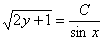 
Ответ: общий интеграл: 
Примечание: общий интеграл любого уравнения можно записать не единственным способом.
задача Коши состоит из следующих этапов:
1) Нахождение общего решение. 2) Нахождение частного решения. 3) Проверка
|
|
|
Пример 4
Найти частное решение дифференциального уравнения 
, удовлетворяющее начальному условию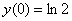 
. Выполнить проверку.
Решение: Сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы 
и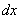 
, а значит, решение упрощается. Разделяем переменные:
Интегрируем уравнение:
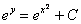
Навешиваем логарифмы:
Итак, общее решение: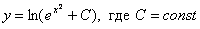 
Найдем частное решение, соответствующее заданному начальному условию .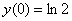 
Ответ: частное решение: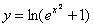 
Пример 5
Решить дифференциальное уравнение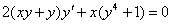 
. Выполнить проверку.
Решение: Данное уравнение допускает разделение переменных. Разделяем переменные:
Интегрируем:
Константу тут не обязательно определять под логарифм, поскольку ничего путного из этого не получится.
Ответ: общий интеграл: 
ЧАСТЬ 2
Однородные дифференциальные уравнения первого порядка
Пример 1 Решить дифференциальное уравнение 
Решение:
Как решить однородное дифференциальное уравнение?
Абсолютно все однородные уравнения можно решить с помощью одной-единственной (!) стандартной замены. Подставляем 
и 
в исходное уравнение :
Что даст такая замена? После данной замены и проведенных упрощений мы гарантировано получим уравнение с разделяющимися переменными. После подстановки проводим максимальные упрощения уравнения:
|
|
|
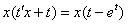
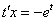
Далее алгоритм работает по накатанной колее уравнения с разделяющимися переменными.
Если 
– это функция, зависящая от «икс», то 
. Таким образом: 
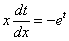
Разделяем переменные:
Переменные разделены, интегрируем:
После того, как уравнение проинтегрировано, нужно провести обратную замену, она тоже стандартна и единственна:
Если , то 
В данном случае: 
Дата добавления: 2021-04-15; просмотров: 65; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!