Задачи, связанные с дифференцированными платежами.
Задача №1.
Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
Решение: Сумма кредита (S), ставка (r) -? %, b=1+0,01r
| Месяц | Долг с % | Выплата | Долг после выплаты |
| 1 | Sb | Sb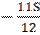 
| 
|
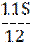
| 2 |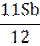 
| 
| 
|
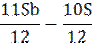
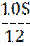
| 3 |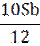 
| 
| 
|
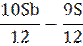
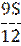
| 4 |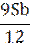 
| 
| 
|
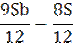
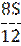
| 5 |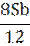 
| 
| 
|
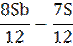
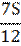
| 6 |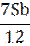 
| 
| 
|
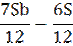
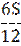
| 7 |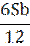 
| 
| 
|
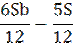
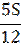
| 8 |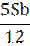 
| 
| 
|
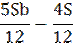
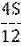
| 9 |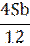 
| 
| 
|
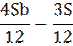
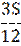
| 10 |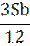 
| 
| 
|
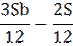
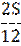
| 11 |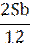 
| 
| 
|
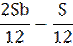
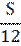
| 12 |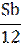 
|
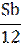
| 0 |
Sb(1+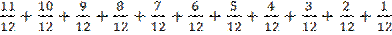 
)-S 
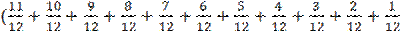)=1,13S
- 
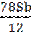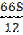= 1,13S /S
- 
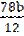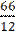= 1,13
78b=1,13*12+66
b=1,02
r=2%
Ответ:2%.
Задача 2.
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
|
|
|
Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Задача 3.
15-го января планируется взять кредит в банке на несколько месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возврастает на 5% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. (решение с помощью формулы суммы арифметической прогрессии)
Нестандартные задачи, связанные с кредитом.
Задача 1.
В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года.
— с февраля по июнь необходимо выплатить часть долга.
|
|
|
— в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб.
— суммы выплат 2020 и 2021 годов равны.
Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей.
Решение: S=6,6
r% =? b=1+0,01r
| Год | Долг с % | Выплата | Долг после выплаты |
| 2017 | Sb | Sb-S | S |
| 2018 | Sb | Sb-S | S |
| 2019 | Sb | Sb-S | S |
| 2020 | Sb | x | Sb-x |
| 2021 | (Sb-x)b= Sb2-xb | x | 0 |
1)Sb2-xb-x=0
2)3Sb-3S+2x=12,6
19,8b-19,8+2x=12,6
x=16,2-9.9b
1) 6,6 b2 –(16,2-9,9b)b=16,2-9,9b
6,6 b2 -16,2b+9,9 b2 =16,2-9,9b
16,5 b2 -6,3b-16,2=0
165 b2 -63b-162=0
D=632+4•162•165=110889
b1=1,2; b2= -0,81не подходит по условию задачи.
Ответ: r =20.
Задача №2.
1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей?
Задача №3.
Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц. Существуют две схемы выплаты кредита.
|
|
|
По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк фиксированную сумму и в результате выплачивает весь долг тремя равными платежами (аннуитетные платежи).
По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину (дифференцированные платежи). Какую схему выгоднее выбрать Анатолию? Сколько рублей будет составлять эта выгода?
Задача №4.
Петр Иванович взял кредит на несколько лет и выплатил его равными ежегодными платежами по 200000 руб. При этом в начале каждого года сумма текущего долга увеличивалась на 10 %, а в конце года производился платёж. Если бы Петр Иванович не делал платежей, то за это время вследствие начисления процентов сумма кредита составила бы 928200 руб. На сколько лет был взят кредит?
|
|
|
Вклады.
Задача №1.
Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу?
Решение:
S=3600 тысяч – сумма вклада
r% - годовые (ежемесячные) проценты, r=10%
b=1+0,01r – коэффициент, b=1,1
n=3 года, х =? – действие
| Год | Вклад с % | Действие | Вклад после действия. |
| 1 год | Sb | +х | Sb+x |
| 2 год | b(Sb+x)= Sb2+xb | +х | Sb2+xb+x |
| 3 год | b(Sb2+xb+x)=Sb3_+хb2+xb | Снял вклад |
Sb3+хb2+xb = 1,485S
х(b2+b) = 1,485S - Sb3
х(1,21+1,1) = 1,485S – 1,331S
2,31х = 0,154*3600
2,31х = 554,4
х = 240
Ответ: 240000.
Задача №2.
Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма будет на счете у Василия через 4 года? (Решение с помощью формулы суммы геометрической прогрессии)
Задача №3.
Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей?
Задача №4.
Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей?
Задача №5.
Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года: часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй – 10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если через три года доход гражданки Васильевой от вложения денег составил 14 520 млн. рублей.
Задача №6.
1 ноября 2017 года Николай открыл в банке счёт «Управляй», вложив S тысяч рублей (S – целое число) сроком на 4 года под 10% годовых. По договору с банком проценты по вкладу должны начисляться 31 октября каждого последующего года. 1 ноября 2019 года и 1 ноября 2020 года Николай планирует снять со счёта 100 тысяч и 50 тысяч рублей соответственно. 1 ноября 2021 года Николай собирается закрыть счёт в банке и забрать все причитающиеся ему деньги. Найдите наименьшее значение S, при котором доход Николая от вложений в банк за эти 4 года окажется более 70 тысяч рублей.
Задача №7.
За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом 11 
и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на 104 
%. Определите срок хранения вклада.
Задача №8
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Дата добавления: 2021-04-15; просмотров: 739; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!