Выпуклость и вогнутость функции
ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
Исследование функции на монотонность
Изучение количественной стороны процессов и явлений природы или техники приводит к установлению и исследованию функциональной зависимости между участвующими в данном явлении или процессе переменными величинами. Если такую функциональную зависимость можно выразить аналитически, в виде формулы, то мы получаем возможность исследовать свойства полученной функции средствами математического анализа.
Функция  называется возрастающей на числовом промежутке
называется возрастающей на числовом промежутке 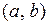 , если взятому из заданного промежутка большему значению аргумента соответствует большее значение функции:
, если взятому из заданного промежутка большему значению аргумента соответствует большее значение функции:
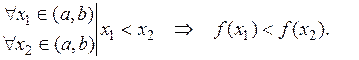
Функция  является убывающей на промежутке
является убывающей на промежутке 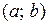 , если выполняется условие:
, если выполняется условие:
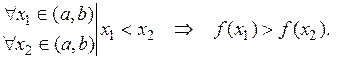
Возрастающая (или убывающая) на промежутке 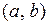 функция
функция  называется монотонной на этом промежутке, а сами промежутки, на которых данная функция возрастает (или убывает), называются промежутками (интервалами) монотонности этой функции.
называется монотонной на этом промежутке, а сами промежутки, на которых данная функция возрастает (или убывает), называются промежутками (интервалами) монотонности этой функции.
Теорема (необходимый признак возрастания (убывания) функции)
1. Если дифференцируемая функция  возрастает на некотором интервале
возрастает на некотором интервале 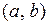 , то производная этой функции неотрицательна на этом интервале:
, то производная этой функции неотрицательна на этом интервале:  при
при  .
.
2. Если дифференцируемая функция  убывает на интервале
убывает на интервале 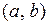 , то её производная неположительна на этом интервале:
, то её производная неположительна на этом интервале:  при
при  .
.
Доказательство. Пусть для определенности  возрастает на интервале
возрастает на интервале 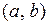 . Выберем произвольно точку
. Выберем произвольно точку  и приращение аргумента
и приращение аргумента  таким образом, чтобы выполнялось условие:
таким образом, чтобы выполнялось условие:  . Тогда
. Тогда
|
|
|
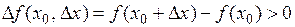 , если
, если 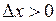 ,
,
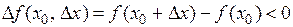 , если
, если 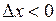 ,
,
откуда следует, что 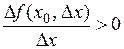 , причём предел такого отношения существует в силу дифференцируемости функции
, причём предел такого отношения существует в силу дифференцируемости функции  на интервале
на интервале 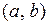 .
.
Поэтому  (при переходе к пределу в неравенстве знак неравенства «ослабевает»), что и требовалось доказать.
(при переходе к пределу в неравенстве знак неравенства «ослабевает»), что и требовалось доказать.
Геометрический смысл теоремы состоит в том, что в каждой точке графика возрастающей дифференцируемой функции  касательная прямая образует с положительным направлением оси (Ox) острый угол или параллельна оси (Ox) (рис. 1). С графиком убывающей дифференцируемой функции
касательная прямая образует с положительным направлением оси (Ox) острый угол или параллельна оси (Ox) (рис. 1). С графиком убывающей дифференцируемой функции  касательная образует тупой угол с положительным направлением оси (Ox) или параллельна ей (рис. 2).
касательная образует тупой угол с положительным направлением оси (Ox) или параллельна ей (рис. 2).
 | |||
 | |||
Рис. 1 Рис. 2
т еорема (достаточный признак монотонности функции)
1. Если производная функции  равна нулю на интервале
равна нулю на интервале 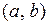 , то функция
, то функция  постоянна на этом интервале:
постоянна на этом интервале:
[  при
при  ]
]  [
[  на
на 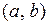 ].
].
2. Если производная функции  положительна на интервале
положительна на интервале 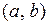 , то функция
, то функция  возрастает на этом интервале:
возрастает на этом интервале:
[ 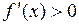 при
при  ]
]  [
[  возрастает на
возрастает на 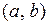 ].
].
|
|
|
3. Если производная функции  отрицательна на
отрицательна на 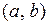 , то функция
, то функция  убывает на этом интервале:
убывает на этом интервале:
[  при
при  ]
]  [
[  убывает на
убывает на 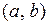 ].
].
Доказательство. Пусть для определенности 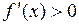 на интервале
на интервале 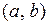 .
.
Выберем любые два значения аргумента  такие, что
такие, что  . Функция
. Функция  удовлетворяет условиям теоремы Лагранжа на отрезке
удовлетворяет условиям теоремы Лагранжа на отрезке  , так как она непрерывна на этом отрезке и дифференцируема во всех его внутренних точках. Тогда по теореме Лагранжа найдётся такая точка
, так как она непрерывна на этом отрезке и дифференцируема во всех его внутренних точках. Тогда по теореме Лагранжа найдётся такая точка  , для которой справедливо равенство
, для которой справедливо равенство  . По условию
. По условию 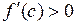 ,
, 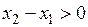 , поэтому
, поэтому  , то есть
, то есть
 , и функция
, и функция  возрастает на промежутке
возрастает на промежутке 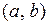 .
.
Пример. Найти интервалы монотонности функции  .
.
Решение. Функция определена при всех действительных  и
и 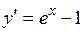 .
.
Неравенство 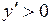 , т.е.
, т.е. 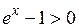 , выполняется при условии
, выполняется при условии  , а неравенство
, а неравенство  (
(  ) – при условии
) – при условии  . Следовательно, функция возрастает на промежутке
. Следовательно, функция возрастает на промежутке  и убывает на промежутке
и убывает на промежутке  .
.
Экстремумы функции
Точка  называется точкой максимума (или точкой минимума) функции
называется точкой максимума (или точкой минимума) функции  , если функция
, если функция  определена в некоторой окрестности
определена в некоторой окрестности 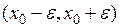 точки
точки  и для любых значений
и для любых значений  выполняется условие:
выполняется условие:  (или
(или  ) (рис. 3, 4).
) (рис. 3, 4).
Значение функции в точке максимума (или минимума) называется максимальным (или минимальным) значением функции или просто её максимумом (минимумом). Максимумы и минимумы функции  называются её экстремумами.
называются её экстремумами.
|
|
|
 | |||
 | |||
Рис. 3 Рис. 4
Теорема (необходимое условие экстремума)
 Если дифференцируемая функция
Если дифференцируемая функция  имеет экстремум в точке
имеет экстремум в точке  , то производная функции в этой точке равна нулю:
, то производная функции в этой точке равна нулю:  .
.
Обратная теорема неверна, так как не всякая точка, в которой производная функции обращается в нуль, является её точкой экстремума.
Пример 1. Для функции  производная
производная
 при
при  , но точка
, но точка  точкой экстремума не является (рис. 5).
точкой экстремума не является (рис. 5).
С другой стороны, если  – точка экстремума некоторой функции
– точка экстремума некоторой функции  , то, очевидно, производная функции в этой точке либо равна нулю, либо не существует. С геометрической точки зрения это означает, что касательная к кривой
, то, очевидно, производная функции в этой точке либо равна нулю, либо не существует. С геометрической точки зрения это означает, что касательная к кривой  в этой точке параллельна оси (Ox) (рис. 6) или не существует (рис. 7).
в этой точке параллельна оси (Ox) (рис. 6) или не существует (рис. 7).
 | |||
 | |||
Рис. 6 Рис. 7
Пример 2. Для функции  точка
точка  является точкой минимума, но её производная в точке
является точкой минимума, но её производная в точке  не существует (рис. 7).
не существует (рис. 7).
Точки, в которых производная функции  обращается в нуль или не существует, называются критическими точками первого рода или точками, «подозрительными на экстремум».
обращается в нуль или не существует, называются критическими точками первого рода или точками, «подозрительными на экстремум».
|
|
|
Теорема об исследовании функции на экстремум по первой производной
(первый достаточный признак экстремума)
Пусть:
1)  – критическая точка функции
– критическая точка функции  ;
;
2) 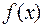 дифференцируема при любых
дифференцируема при любых  ;
;
3)  непрерывна в точке
непрерывна в точке  .
.
Тогда: если при переходе через точку  производная меняет знак с плюса (+) на минус (–), то
производная меняет знак с плюса (+) на минус (–), то  – точка максимума функции
– точка максимума функции  , в случае же замены знака производной с минуса (–) на плюс (+) получается точка минимума.
, в случае же замены знака производной с минуса (–) на плюс (+) получается точка минимума.
Доказательство. По определению непрерывной функции имеем:
 .
.
Пусть при переходе через точку  производная меняет знак с (+) на (–). Так как
производная меняет знак с (+) на (–). Так как  на промежутке
на промежутке 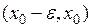 , то функция
, то функция  возрастает на
возрастает на 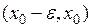 до значения
до значения  , таким образом,
, таким образом,  на
на 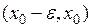 . Аналогично:
. Аналогично: 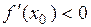 на
на 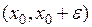

 убывает на промежутке
убывает на промежутке 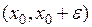 от значения
от значения  , то есть
, то есть  и на
и на 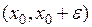 . Получили, что неравенство
. Получили, что неравенство  выполняется для всех значений аргумента
выполняется для всех значений аргумента  , а это означает, что
, а это означает, что  – точка максимума функции
– точка максимума функции  .
.
Пример 3. Найти промежутки монотонности и экстремумы функции
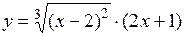 .
.
Решение. Функция определена при всех действительных значениях аргумента:  ;
;  . Критическими точками первого рода для данной функции являются
. Критическими точками первого рода для данной функции являются  (так как
(так как 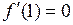 ) и
) и  (так как
(так как  не существует).
не существует).

Рис. 8
Так как  в промежутках (-¥; 1) и (2; +¥), то
в промежутках (-¥; 1) и (2; +¥), то  возрастает на этих промежутках; на интервале (1; 2) функция убывает, поскольку там
возрастает на этих промежутках; на интервале (1; 2) функция убывает, поскольку там  .
.
Согласно первому признаку экстремума:
 – точка максимума,
– точка максимума, 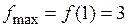 – максимум функции;
– максимум функции;
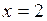 – точка минимума,
– точка минимума, 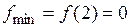 – минимум функции.
– минимум функции.
Теорема об исследовании функции на экстремум по второй производной
(второй достаточный признак экстремума)
Пусть:
1)  , т.е.
, т.е.  – стационарная точка функции
– стационарная точка функции  ;
;
2) 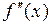 непрерывна в точке
непрерывна в точке  ;
;
3)  .
.
Тогда точка  будет точкой максимума в случае, если
будет точкой максимума в случае, если  , и минимума, если
, и минимума, если 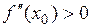 .
.
Доказательство. Рассмотрим случай, когда  . Так как вторая производная
. Так как вторая производная 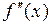 непрерывна в этой точке, то она, очевидно, сохраняет знак в некоторой её окрестности
непрерывна в этой точке, то она, очевидно, сохраняет знак в некоторой её окрестности 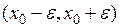 :
:  для всех
для всех  . По достаточному признаку монотонности функции можно сделать вывод, что первая производная
. По достаточному признаку монотонности функции можно сделать вывод, что первая производная  убывает на всём промежутке
убывает на всём промежутке 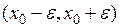 . Если
. Если  , то левее точки
, то левее точки  , при
, при  ,
,  (+), а правее, при
(+), а правее, при 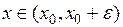 ,
,  (–). Согласно первому признаку экстремума точка
(–). Согласно первому признаку экстремума точка  будет точкой максимума функции
будет точкой максимума функции  .
.
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 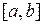 , следовательно, по теореме Вейерштрасса она достигает на
, следовательно, по теореме Вейерштрасса она достигает на 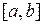 наибольшего и наименьшего значений, причем наибольшего и наименьшего значений
наибольшего и наименьшего значений, причем наибольшего и наименьшего значений  достигает либо в критических точках, расположенных внутри отрезка
достигает либо в критических точках, расположенных внутри отрезка 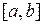 или на его границах
или на его границах 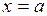 ,
,  . Сформулируем правило нахождения наименьшего и наибольшего значений непрерывной на отрезке
. Сформулируем правило нахождения наименьшего и наибольшего значений непрерывной на отрезке 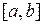 функции
функции  :
:
1) найти критические точки функции  , содержащиеся внутри отрезка
, содержащиеся внутри отрезка 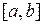 , и вычислить значения функции в этих точках;
, и вычислить значения функции в этих точках;
2) найти  ,
,  – значения функции на границах отрезка;
– значения функции на границах отрезка;
3) выбрать среди полученных значений наименьшее и наибольшее.
Пример 4. Найти наибольшее и наименьшее значения функции 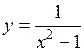 на отрезке
на отрезке  .
.
Решение.
1) Функция определена и непрерывна во всех точках отрезка  , производная
, производная 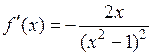 обращается в нуль в точке
обращается в нуль в точке  , принадлежащей отрезку
, принадлежащей отрезку  , и не существует в точках
, и не существует в точках  , расположенных вне данного отрезка.
, расположенных вне данного отрезка.
2) Найдем значения функции в критической точке  и граничных точках отрезка
и граничных точках отрезка  :
:  ,
,  ,
,  .
.
3) Функция принимает наименьшее значение на концах отрезка:
 ,
,
а наибольшее значение – в точке  :
:  .
.
Выпуклость и вогнутость функции
Непрерывная на интервале 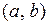 функция
функция  называется вогнутой (или выпуклой вниз), если соответствующая дуга её графика расположена выше любой из касательных, проведенных к нему в точках
называется вогнутой (или выпуклой вниз), если соответствующая дуга её графика расположена выше любой из касательных, проведенных к нему в точках  при всех
при всех  (рис. 9). Непрерывная на интервале
(рис. 9). Непрерывная на интервале 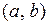 функция
функция  называется выпуклой (или выпуклой вверх), если соответствующая дуга её графика расположена ниже любой из касательных, проведенных к нему в точках
называется выпуклой (или выпуклой вверх), если соответствующая дуга её графика расположена ниже любой из касательных, проведенных к нему в точках  при всех
при всех  (рис. 10).
(рис. 10).
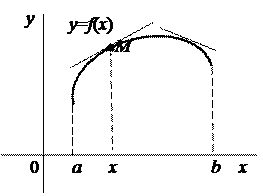 |
Рис. 9 Рис. 10
Рис. 11 Рис. 12
 |
Аналитически определение вогнутой функции можно охарактеризовать следующим условием: при любых
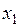 и
и 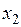 , лежащих в интервале
, лежащих в интервале  , справедливо неравенство
, справедливо неравенство 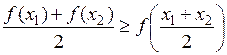 (рис.11); для выпуклой функции подобное условие имеет вид:
(рис.11); для выпуклой функции подобное условие имеет вид:  .
.
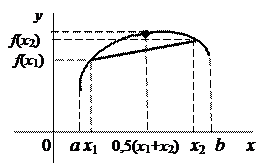
 |
Рассмотрим необходимые и достаточные условия выпуклости и вогнутости функции на интервале.
Теорема о необходимом условии вогнутости или выпуклости функции
Если существует вторая производная вогнутой (или выпуклой) на промежутке 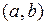 функции
функции  , то она на этом промежутке будет неотрицательной (или неположительной):
, то она на этом промежутке будет неотрицательной (или неположительной):
 (или
(или 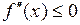 ) для всех
) для всех 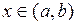 .
.
Теорема о достаточных условиях выпуклости или вогнутости функции на интервале)
1. Если 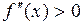 при любом
при любом  , то функция
, то функция  является вогнутой на интервале
является вогнутой на интервале 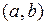 .
.
2. Если же  при любом
при любом  , то функция
, то функция  выпукла на интервале
выпукла на интервале 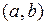 .
.
Доказательство. Пусть  на интервале
на интервале 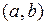 . Выберем два произвольных значения аргумента
. Выберем два произвольных значения аргумента 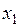 и
и  из интервала
из интервала 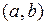 , таких, что
, таких, что 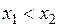 , и образуем отрезок
, и образуем отрезок  . Из факта существования второй производной
. Из факта существования второй производной  функции
функции  на
на 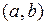 следует, что первая производная
следует, что первая производная  и сама функция
и сама функция  будут дифференцируемыми и непрерывными на этом интервале, а, следовательно, и на отрезке
будут дифференцируемыми и непрерывными на этом интервале, а, следовательно, и на отрезке  .
.
Рассмотрим разность  и преобразуем её, используя формулу Лагранжа, применяемую сначала к самой функции
и преобразуем её, используя формулу Лагранжа, применяемую сначала к самой функции  , а затем к её производной
, а затем к её производной  :
:
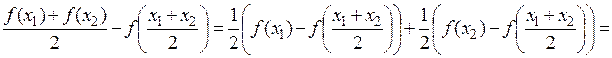


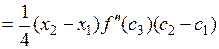 ,
,
где 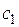 и
и  – точки, существование которых на соответствующих промежутках
– точки, существование которых на соответствующих промежутках 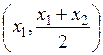 и
и  регламентируется теоремой Лагранжа, а точка
регламентируется теоремой Лагранжа, а точка  по той же причине существует на интервале
по той же причине существует на интервале  . Оценим величину указанной выше разности, учитывая, что
. Оценим величину указанной выше разности, учитывая, что 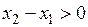 ,
,  ,
,  :
:
 ,
,
откуда получаем, что  для любых
для любых  .
.
Это означает, что функция  является выпуклой на интервале
является выпуклой на интервале 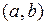 .
.
Точка 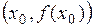 называется точкой перегиба графика функции
называется точкой перегиба графика функции  , если эта точка отделяет выпуклую часть графика от вогнутой. Если вторая производная функции в точке
, если эта точка отделяет выпуклую часть графика от вогнутой. Если вторая производная функции в точке  равна нулю или не существует, то такая точка называется критической точкой второго рода функции
равна нулю или не существует, то такая точка называется критической точкой второго рода функции  или точкой, «подозрительной на перегиб».
или точкой, «подозрительной на перегиб».
Теорема (первое достаточное условие наличия точек перегиба)
Пусть:
1)  – критическая точка (второго рода) функции
– критическая точка (второго рода) функции  ;
;
2) существует 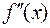 при любых
при любых  ;
;
3)  непрерывна в точке
непрерывна в точке  ;
;
4) при переходе аргумента через точку  вторая производная
вторая производная  изменяет свой знак.
изменяет свой знак.
Тогда  является абсциссой точки перегиба функции
является абсциссой точки перегиба функции  .
.
Доказательство теоремы аналогично доказательству первого достаточного признака экстремума функции. 1
Теорема (второе достаточное условие наличия точки перегиба)
Если 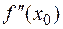 = 0, а третья производная
= 0, а третья производная 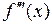 непрерывна и отлична от нуля в точке
непрерывна и отлична от нуля в точке  , то точка с координатами
, то точка с координатами 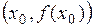 является точкой перегиба графика функции
является точкой перегиба графика функции  .
.
Пример. Найти интервалы выпуклости, вогнутости и точки перегиба функции
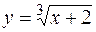 .
.
Решение. Функция определена для всех действительных значений аргумента:  . Найдём производные данной функции:
. Найдём производные данной функции:
 ,
,  .
.
Вторая производная не обращается в нуль ни при каком значении  , но не существует для
, но не существует для  .
.
 |
Рис. 13
Так как  при
при 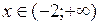 , то промежуток
, то промежуток  является интервалом выпуклости функции
является интервалом выпуклости функции  . Промежуток
. Промежуток 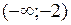 будет интервалом вогнутости функции, потому что
будет интервалом вогнутости функции, потому что  при
при  . Точка перегиба графика имеет координаты
. Точка перегиба графика имеет координаты  .
.
3.4. Асимптоты графика функции
Прямая  называется асимптотой графика функции
называется асимптотой графика функции  , если расстояние от переменной точки
, если расстояние от переменной точки  графика до этой прямой при неограниченном удалении точки М от начала координат стремится к нулю (рис. 14):
графика до этой прямой при неограниченном удалении точки М от начала координат стремится к нулю (рис. 14):
 при условии, что
при условии, что 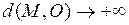
 .
.
Асимптоты бывают вертикальные и невертикальные (или наклонные). Существование невертикальной асимптоты для функции  означает, что при
означает, что при  (
(  ) (
) (  стремится к ¥ в одном или в двух направлениях) функция ведет себя «почти как линейная функция», то есть отличается от линейной функции
стремится к ¥ в одном или в двух направлениях) функция ведет себя «почти как линейная функция», то есть отличается от линейной функции  на бесконечно малую
на бесконечно малую 
Рис. 15 (рис. 15): 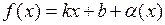 .
.
 Пример 1. Дана функция
Пример 1. Дана функция
 .
.
| 2x2 + 3x + 4 | x + 1 | |||||
| 2x2 + 2x | 2x + 1 | |||||
|
|
| |||||
| x + 4 |
| ||||
| x + 1 |
| |||||
|
Рис. 15
Так как  , то прямая
, то прямая 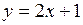 является асимптотой графика функции
является асимптотой графика функции  .
.
Теорема об условиях существования невертикальных асимптот
Для того чтобы прямая  являлась невертикальной асимптотой графика функции
являлась невертикальной асимптотой графика функции  при
при 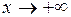 или (и) при
или (и) при 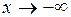 , необходимо и достаточно, чтобы существовали нижеуказанные пределы и выполнялись условия:
, необходимо и достаточно, чтобы существовали нижеуказанные пределы и выполнялись условия:
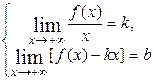 или (и)
или (и) 
Если существует асимптота при 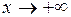 , то её называют правосторонней, в случае, когда
, то её называют правосторонней, в случае, когда 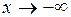 , левосторонней, а в случае
, левосторонней, а в случае  асимптота будет двусторонней.
асимптота будет двусторонней.
Доказательство.
1) Необходимость существования асимптоты.
Пусть для определенности  – асимптота графика функции
– асимптота графика функции  при
при  , то есть
, то есть 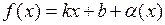 , причём
, причём  . Тогда
. Тогда
 ,
,
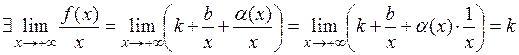 ,
, 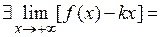
 ,
,
что и требовалось доказать.
2) Достаточность существования асимптоты практически очевидна: если существуют конечные пределы  и
и 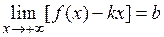 , то существует и
, то существует и  , откуда следует, что
, откуда следует, что 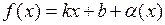 , где
, где  есть бесконечно малая функция при
есть бесконечно малая функция при  , а это означает, что прямая
, а это означает, что прямая  является невертикальной асимптотой графика функции
является невертикальной асимптотой графика функции  .
.
Если хотя бы один из пределов, предназначенных для нахождения коэффициентов k и b , бесконечен, то невертикальная асимптота графика функции не существует. В случае, когда k = 0, получаем горизонтальную асимптоту  как частный случай невертикальной асимптоты.
как частный случай невертикальной асимптоты.
Теорема об условиях существования вертикальных асимптот
Для того чтобы прямая  являлась вертикальной асимптотой графика функции
являлась вертикальной асимптотой графика функции  , необходимо и достаточно, чтобы выполнялось одно из условий:
, необходимо и достаточно, чтобы выполнялось одно из условий:
или 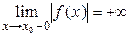 ,
,
или 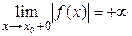 ,
,
или  .
.
В первых двух случаях асимптота будет односторонней, в третьем случае асимптота двусторонняя. Вертикальные асимптоты графика следует искать в точках разрыва второго рода (с бесконечным пределом) или в граничных точках области определения функции.
Пример 2. Найти асимптоты функции  .
.
Решение. Логарифмическая функция определена для всех положительных значений аргумента:  .
.
1) Найдем правосторонний предел функции в граничной точке области определения  :
:  (по-другому:
(по-другому:  ), откуда следует, что прямая
), откуда следует, что прямая  является правосторонней вертикальной асимптотой графика данной функции.
является правосторонней вертикальной асимптотой графика данной функции.
2) Невертикальных асимптот у этой функции нет, так как  ,
,  .
.
Пример 3. Найти асимптоты графика функции 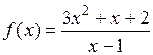 .
.
Решение. Областью определения функции является множество 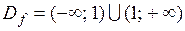 .
.
1) Так как  , то прямая
, то прямая 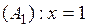 является (двусторонней) вертикальной асимптотой графика данной функции.
является (двусторонней) вертикальной асимптотой графика данной функции.
2) Поскольку  ,
,
 ,
,
то 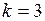 ,
,  , и двусторонняя невертикальная асимптота
, и двусторонняя невертикальная асимптота 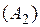 задается уравнением
задается уравнением  .
.
План общего исследования функции
Ранее мы рассмотрели, каким образом можно исследовать свойства функции, используя её производную и разнообразные предельные переходы. Как итог, укажем основные шаги плана полного исследования функции, предназначенного для построения её графика.
План полного исследования функции
1) Найти область определения функции.
2) Исследовать функцию на четность – нечетность и периодичность.
3) Исследовать функцию на непрерывность: указать интервалы непрерывности, точки разрыва, род разрыва.
4) Найти вертикальные и невертикальные асимптоты графика функции.
5) Найти интервалы монотонности и экстремумы функции (с помощью первой производной).
6) Найти интервалы выпуклости и вогнутости функции, указать точки перегиба графика функции (с помощью второй производной).
7) Найти точки пересечения графика функции с осями координат, а при необходимости и какие-либо другие точки. Можно (не обязательно!) указать интервалы знакопостоянства функции.
8) По результатам исследования построить график функции.
Пример 1. Провести полное исследование функции  и построить её график.
и построить её график.
Решение.
1) Областью определения функции является множество 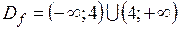 .
.
2) Функция не является ни чётной, ни нечётной (общего вида), это непериодическая функция.
3) Числовые промежутки  и
и  будут интервалами непрерывности данной функции (по теореме о непрерывности элементарной функции).
будут интервалами непрерывности данной функции (по теореме о непрерывности элементарной функции).
Найдем односторонние пределы функции в точке  :
:
 ;
; 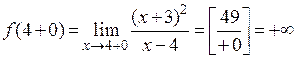 ;
;
поэтому точка  является точкой разрыва второго рода.
является точкой разрыва второго рода.
4) Так как точка  – точка разрыва второго рода, то прямая
– точка разрыва второго рода, то прямая 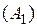 , заданная уравнением
, заданная уравнением  , будет вертикальной асимптотой графика функции.
, будет вертикальной асимптотой графика функции.
Уравнение невертикальной (наклонной) асимптоты ищем в виде 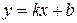 , где
, где
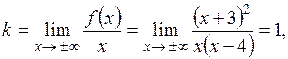
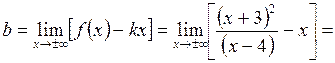
 .
.
Таким образом, существует единственная (двусторонняя) невертикальная асимптота 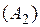 , заданная уравнением
, заданная уравнением 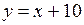 .
.
5) Исследуем функцию на монотонность и экстремумы. Найдём производную
 .
.
Из условия  следует, что
следует, что 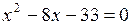 . Решая это уравнение, получим две критические точки первого рода:
. Решая это уравнение, получим две критические точки первого рода:  . Производная
. Производная 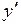 не существует при
не существует при 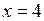 , но эта точка не входит в область определения функции.
, но эта точка не входит в область определения функции.
На числовых промежутках 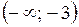 и
и  выполняется условие
выполняется условие  , следовательно, функция возрастает в этих интервалах; на промежутках
, следовательно, функция возрастает в этих интервалах; на промежутках  и
и  выполняется условие
выполняется условие  , то есть функция там убывает. В точке
, то есть функция там убывает. В точке  функция имеет (локальный) максимум:
функция имеет (локальный) максимум:  . В точке
. В точке  имеется (локальный) минимум:
имеется (локальный) минимум:  .
.
6) Исследуем функцию на выпуклость, вогнутость и наличие точек перегиба. Для этого найдём вторую производную
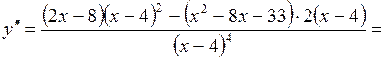
 .
.
Вторая производная 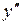 не существует при
не существует при  .
.
Очевидно, что на промежутке  выполняется условие
выполняется условие  , и на этом промежутке кривая будет выпуклой; на промежутке
, и на этом промежутке кривая будет выпуклой; на промежутке  выполняется условие
выполняется условие 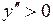 , то есть на этом интервале кривая будет вогнутой. Точек перегиба графика функции нет.
, то есть на этом интервале кривая будет вогнутой. Точек перегиба графика функции нет.
7) Точками пересечения графика данной функции с осями координат являются точки с координатами  и
и  . При
. При  , то есть на промежутке
, то есть на промежутке  функция принимает положительные значения, при
функция принимает положительные значения, при  , или на промежутке
, или на промежутке  функция отрицательна. Это и есть интервалы знакопостоянства данной функции.
функция отрицательна. Это и есть интервалы знакопостоянства данной функции.
8) По результатам исследования построим график функции (рис 16).

Рис. 16
Пример 2. Провести полное исследование функции 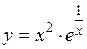 и построить её график.
и построить её график.
1) Областью определения функции является множество  .
.
2) Данная функция является функцией общего вида, так как, несмотря на симметричность области определения 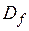 относительно начала координат,
относительно начала координат, 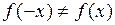 ,
,  ; это непериодическая функция.
; это непериодическая функция.
3) Числовые промежутки  и
и  – интервалы непрерывности функции; точка
– интервалы непрерывности функции; точка  будет точкой разрыва второго рода (справа), так как
будет точкой разрыва второго рода (справа), так как
 ;
;
 .
.
4) Прямая  - вертикальная (справа) асимптота графика функции.
- вертикальная (справа) асимптота графика функции.
Невертикальных асимптот нет, так как 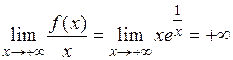 ,
,
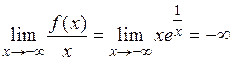 .
.
5) Исследуем функцию на монотонность и экстремумы. Для этого найдём первую производную функции
 ;
;
 при
при  , не существует
, не существует  в точке
в точке 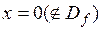 , поэтому имеется одна критическая точка первого рода. Учитывая знак производной на отдельных промежутках (рис. 17), получим, что интервалами убывания функции будут
, поэтому имеется одна критическая точка первого рода. Учитывая знак производной на отдельных промежутках (рис. 17), получим, что интервалами убывания функции будут  и
и 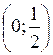 , а интервалом возрастания – промежуток
, а интервалом возрастания – промежуток 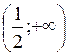 .
.
 |
Рис. 17
Точка 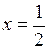 - точка минимума функции; сам минимум функции равен
- точка минимума функции; сам минимум функции равен  .
.
6) Исследуем функцию на выпуклость, вогнутость и наличие точек перегиба:
 ;
;
очевидно, что 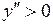 при всех значениях аргумента из области определения
при всех значениях аргумента из области определения 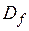 , следовательно, интервалами вогнутости функции будут промежутки
, следовательно, интервалами вогнутости функции будут промежутки  и
и  ; точек перегиба нет.
; точек перегиба нет.
7) С осями координат график функции не пересекается. Функция положительна во всей своей области определения. Для более точной картины можно рассмотреть дополнительные точки графика: 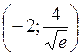 ,
,  ,
,  .
.
8) Построим график функции 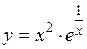 (рис. 18) .
(рис. 18) .

Рис. 18
Контрольные вопросы
1. Дайте определение возрастающей или убывающей функции.
2. В чём состоит необходимый признак монотонности функции на интервале? Поясните геометрический смысл этого признака.
3. Сформулируйте теорему о достаточных условиях постоянства, возрастания и убывания функции на интервале и приведите примеры её применения.
4. Дайте определение точки экстремума (максимума и минимума) функции, максимума и минимума функции. В чём состоит отличие максимального или минимального значений функции от её наибольшего и наименьшего значений?
5. Сформулируйте необходимый признак экстремума функции. Приведите примеры, подтверждающие, что он не является достаточным.
6. В каком случае точка называется критической (первого рода), стационарной для функции  ?
?
7. В чем состоит первый достаточный признак экстремума?
8. Укажите правило исследования функции на монотонность и экстремумы.
9. В чем состоит второй достаточный признак экстремума?
10. Как найти наибольшее и наименьшее значения непрерывной функции на заданном отрезке, содержащемся в области определения функции?
11. Дайте определение выпуклости и вогнутости графика функции  на заданном промежутке. Запишите формулы, иллюстрирующие аналитическую зависимость между значениями выпуклой или вогнутой на интервале функции.
на заданном промежутке. Запишите формулы, иллюстрирующие аналитическую зависимость между значениями выпуклой или вогнутой на интервале функции.
12. Сформулируйте теоремы о необходимых и достаточных условиях выпуклости или вогнутости функции и поясните, в чем их различие.
13. В каком случае точку графика функции можно назвать точкой перегиба? Как найти критические точки (второго рода) функции  ?
?
14. Сформулируйте какой-нибудь достаточный признак наличия точки перегиба графика. Наблюдается ли здесь аналогия с соответствующими действиями по отысканию экстремумов фугкции?
15. Дайте определение асимптоты графика функции. Какими бывают асимптоты? По какому признаку они классифицируются?
16. Как получить уравнения вертикальных и невертикальных асимптот графика функции  ? В каком случае можно утверждать, что вертикальные или невертикальные асимптоты графика не существуют?
? В каком случае можно утверждать, что вертикальные или невертикальные асимптоты графика не существуют?
17. Перечислите основные шаги плана полного исследования свойств функции с целью последующего построения её графика. Уточните порядок действий на каждом этапе решения такой задачи.
Задачи к главе 3
3.1. Найти промежутки убывания и возрастания функции:
1)  ; ;
| 2) 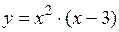 ; ;
|
3)  ; ;
| 4) 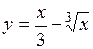 ; ;
|
5) 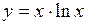 ; ;
| 6)  ; ;
|
7) 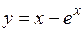 ; ;
| 8)  ; ;
|
9) 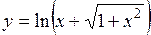 ; ;
| 10)  . .
|
3.2. Показать, что функция  возрастает в интервале (0; 1) и убывает в интервале (1; 2).
возрастает в интервале (0; 1) и убывает в интервале (1; 2).
3.3. Показать, что функция  везде убывает.
везде убывает.
3.4. Найти экстремумы функций:
1) 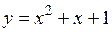 ; ;
| 2)  ; ;
|
3)  ; ;
| 4) 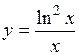 ; ;
|
5) 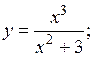
| 6)  ; ;
|
7) 
| 8)  ; ;
|
9)  ; ;
| 10)  . .
|
3.5. Найти наибольшее и наименьшее значения функций на указанных числовых промежутках:
1)  ; [-2, 2];
; [-2, 2];
2)  ; [0, 4];
; [0, 4];
3)  ; [-1, 2];
; [-1, 2];
4) 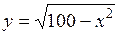 ; [-6, 8];
; [-6, 8];
5)  ;
;  ;
;
6)  ; (0, 1];
; (0, 1];
7)  ; [-1, 1];
; [-1, 1];
8)  ;
;  ;
;
9)  ;
; 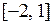 .
.
3.6. Найти число, которое, будучи сложено со своим квадратом, дает наименьшую сумму.
3.7. Найти положительное число, которое, будучи сложено с обратным ему числом, дает наименьшую сумму.
3.8. Требуется изготовить ящик (без крышки) с прямоугольным основанием и заданным объемом 36, отношение сторон основания которого равнялось бы числу 2. Каковы должны быть размеры ящика, чтобы его поверхность была наименьшей?
3.9. Через какую точку эллипса  следует провести касательную, чтобы площадь треугольника, составленного этой касательной и осями координат, была наименьшей?
следует провести касательную, чтобы площадь треугольника, составленного этой касательной и осями координат, была наименьшей?
3.10. Число 36 разложить на два таких множителя, чтобы сумма их квадратов была наименьшей.
3.11. Требуется изготовить ящик с крышкой, объем которого был бы равен 72 см3, причем стороны основания относились бы, как 1:2. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
3.12. Расходы на топливо для топки теплохода пропорциональны кубу его скорости. Известно, что при скорости в 10 км/ч расходы на топливо составляют 30 руб. в час, остальные же расходы (не зависящие от скорости) составляют 480 руб. в час. При какой скорости теплохода общая сумма расходов на 1 км пути будет наименьшей? Какова будет при этом сумма расходов в час?
3.13. Найти точки перегиба и интервалы вогнутости (выпуклости) функций:
1)  ; ;
| 2) 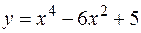 ; ;
| 3)  ; ;
|
4) 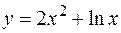 ; ;
| 5) 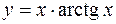 ; ;
| 6)  ; ;
|
7)  ; ;
| 8) 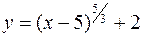 ; ;
| 9)   . .
|
3.14. Показать, что линия  имеет три точки перегиба, лежащие на одной прямой.
имеет три точки перегиба, лежащие на одной прямой.
3.15. Выяснить вид графика функции; если известно, что в интервале (а; b):
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  . .
|
3.16. Найти асимптоты графиков следующих функций:
1)  ; ;
| 2)  ; ;
|
3) 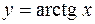 ; ;
| 4) 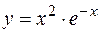 ; ;
|
5)  ; ;
| 6)  ; ;
|
7)  ; ;
| 8)  ; ;
|
9)  ; ;
| 10)  . .
|
3.17. Провести полное исследование функций и построить их графики:
1)  ; ;
| 2)  ; ;
|
3)  ; ;
| 4)  ; ;
|
5) 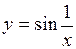 ; ;
| 6) 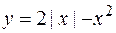 ; ;
|
7)  ; ;
| 8)  ; ;
|
9) 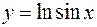 ; ;
| 10) 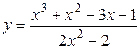 . .
|
Дата добавления: 2021-04-05; просмотров: 178; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
