Условия существования интегрирующего множителя
Дифференциальные уравнения
1. ДУ: порядок, частное решение, общее решение, общий интеграл, задача Коши.
1.Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию y = f(x) и ее производные yʹ, yʹʹ,…y(n).Символическая запись ДУ:F=( yʹ, yʹʹ,…y(n))=0 .
Д.у.-ур-е в кот неизвестная ф-ция y нах под знаком производной (№: yʹ+5y=3x)
2.Порядком д.у. наз-ся порядок наивысшей производной, входящей в ур-е.
Если искомая функция у = f(x) есть функция одной независимой переменной, то ДУ называется обыкновенным ДУ (иначе ДУ называется ДУ в частных производных).
Решением или интегралом ДУ называется всякая дифференцируемая функция y = j(x), которая, будучи подставлена в уравнение, обращает его в тождество.
График решения ДУ (график функции у = f(x)) называется интегральной кривой.
Все д.у. делятся на 2 класса:
1)обыкновенные-ур-я в кот искомая неизв ф-ция y явл-ся функцией одного аргумента y=f(x)
2)д.у.в частных производных- -//- нескольких аргументов z=f(x,y)
3.Решением д.у. явл-ся любая ф-ция y=j (x), кот при подстановке в ур-е обращает его в строгое рав-во.
№: y=x3; yʹ=3x2
3y-xyʹ=0; 3x3-x3x2=0; 0=0
Поскольку реш-е д.у связано с операцией интегрирования,то это приводит к появлению произвольной постоянной С.
При реш-и д.у. первого порядка появл-ся одна произвольная постоянная С.
-//- n-ного порядка интегрирование повторяется n раз, поэтому в реш-и будет содержаться n произв пост С С1, С2, С3,… Сn,
|
|
|
Общим решением д.у. n-ого порядка называется функция: y= j (x, С1, С2, С3,… Сn), кот зависит от n-произвольных постоянных и удовл д.у. при любыхзначениях С1, С2, С3,… Сn,
Частным реш-ем д.у. n-ого порядка называется любая функция, полученная из общего решения д.у. при конкретных значениях произвольных постоянных.
Для нахождения частного из общего необх исп заданные заранее начальные усл-я.
№: нач усл-я: при х=х0→у=у0, yʹ= у0ʹ, yʹʹ= у0ʹʹ
y(n)-порядок производной yn-степень
Если дифференциальное уравнение первого порядка F(х; у; у') = 0 задано вместе с начальным для него условием 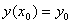 , То говорят, что для этого уравнения задана Задача Коши:
, То говорят, что для этого уравнения задана Задача Коши:
 (2.1)
(2.1)
Решить её - это значит найти те частные решения 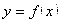 дифференциального уравнения F(х; у; у') = 0 , которые еще удовлетворяют и заданному начальному условию
дифференциального уравнения F(х; у; у') = 0 , которые еще удовлетворяют и заданному начальному условию 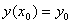 . С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения
. С точки зрения рисунка 6.2 решить задачу Коши (2.1) – это значит найти уравнения 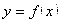 всех интегральных кривых дифференциального уравнения F(х; у; у') = 0, проходящих через начальную точку
всех интегральных кривых дифференциального уравнения F(х; у; у') = 0, проходящих через начальную точку 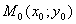 .
.
2. Теорема существования и единственности решения ДУ 1-го порядка
Пусть имеем дифференциальное уравнение первого порядка: y′ = f(x, y). Для такого уравнения Теорема о существовании и единственности решения принимает вид:
|
|
|
| Теорема: (1.1) | Если функция и ее частная производная  непрерывны в некоторой области D плоскости OXY, содержащей точку (x0,y0), то существует единственное решение этого уравнения y=φ(x), удовлетворяющее условию: φ(x0)=y0. непрерывны в некоторой области D плоскости OXY, содержащей точку (x0,y0), то существует единственное решение этого уравнения y=φ(x), удовлетворяющее условию: φ(x0)=y0.
|
3. ДУ с разделяющимися переменными.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
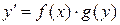 (2)
(2)
или уравнение вида:
 (3)
(3)
Чтобы уравнения (2) и (3) можно было проинтегрировать, необходимо привести их к уравнениям с разделёнными переменными, т.е. при дифференциалах dx и dy должны быть множители, зависящие соответственно от x и от y.
Решим уравнение (2) в общем виде:

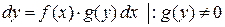
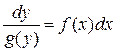
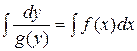
Пусть 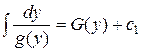 , а
, а 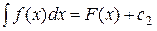 , тогда выражение
, тогда выражение
 или
или  , где
, где 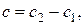 является интегралом уравнения (2). Остается проверить, что не потеряны решения при делении уравнения на выражения, зависящие от переменных. Решим уравнение
является интегралом уравнения (2). Остается проверить, что не потеряны решения при делении уравнения на выражения, зависящие от переменных. Решим уравнение  . Если оно имеет решение, являющееся и решением уравнения (2), то оно тоже будет присоединено к общему интегралу этого уравнения.
. Если оно имеет решение, являющееся и решением уравнения (2), то оно тоже будет присоединено к общему интегралу этого уравнения.
Решим уравнение (3) в общем виде:
|
|
|
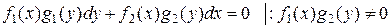


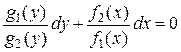
 уравнение с разделенными переменными
уравнение с разделенными переменными


 общий интеграл уравнения (3)
общий интеграл уравнения (3)
К полученному интегралу могут быть добавлены решения уравнений:  и
и  , если они являются для заданного уравнения решениями.
, если они являются для заданного уравнения решениями.
Некоторые дифференциальные уравнения можно привести к уравнениям с разделяющимися переменными. Например, уравнения вида:
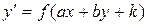 или
или 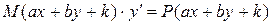 ,
,
где  и
и 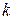 – некоторые числа, приводят к виду (2) или (3) с помощью замены:
– некоторые числа, приводят к виду (2) или (3) с помощью замены:

4. Однородные ДУ 1-го порядка.
Уравнение первого порядка вида 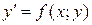 называется однородным, если его правая часть
называется однородным, если его правая часть  является однородной функцией нулевого измерения, т.е. при любом
является однородной функцией нулевого измерения, т.е. при любом  справедливо равенство:
справедливо равенство: 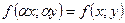 .
.
Замечание 1. Уравнение 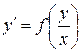 является однородным, так как функция
является однородным, так как функция 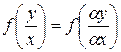 удовлетворяет определению однородности нулевого измерения.
удовлетворяет определению однородности нулевого измерения.
Уравнение вида
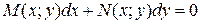
называется однородным, если  однородные функции одного измерения однородности, т.е.
однородные функции одного измерения однородности, т.е.  и
и 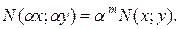
5. Линейные ДУ 1-го порядка и уравнение Бернулли.
Уравнение вида:
 (1)
(1)
где  и
и 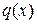 – заданные непрерывные функции на
– заданные непрерывные функции на  называется линейным дифференциальным уравнением (ЛДУ). Если
называется линейным дифференциальным уравнением (ЛДУ). Если  при
при 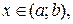 то уравнение имеет вид:
то уравнение имеет вид:
|
|
|
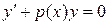
и называется линейным однородным дифференциальным уравнением (ЛОДУ). А если  при
при 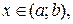 то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
Уравнение вида
 где
где  и
и 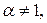 (4)
(4)
называется уравнением Бернулли с показателем  .
.
Уравнение (4) приводится к ЛНДУ(1) с помощью замены:

После этой замены уравнение (1) приводится к следующему:
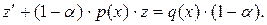
Это уравнение ЛНДУ относительно функции  Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции
Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции 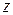 , решать методом замены Бернулли непосредственно. При этом функция
, решать методом замены Бернулли непосредственно. При этом функция 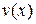 будет частным решением уравнения
будет частным решением уравнения

а функция 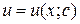 будет находиться из уравнения
будет находиться из уравнения
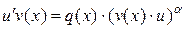 .
.
Замечание 1. При таком решении при  решение
решение  будет всегда потеряно.
будет всегда потеряно.
Замечание 2. Некоторые дифференциальные уравнения первого порядка становятся линейными или уравнениями Бернулли, если в них поменять ролями искомую функцию 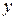 и независимую переменную
и независимую переменную 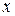 .
.
6. ДУ в полных дифференциалах. Формулировка аналитического признака полного дифференциала.
Если в уравнении
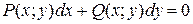 (1)
(1)
левая часть есть полный дифференциал некоторой функции  то оно называется дифференциальным уравнением в полных дифференциалах. Тогда это уравнение можно переписать в виде:
то оно называется дифференциальным уравнением в полных дифференциалах. Тогда это уравнение можно переписать в виде: 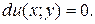 Следовательно, его общий интеграл есть
Следовательно, его общий интеграл есть  где
где 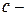 произвольная постоянная.
произвольная постоянная.
Необходимым и достаточным условием того, чтобы выражение 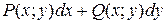 было полным дифференциалом функции
было полным дифференциалом функции  является равенство:
является равенство:
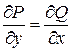 для
для 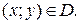
Итак, чтобы решить дифференциальное уравнение (1), надо найти функцию  для которой
для которой  , и записать общий интеграл этого уравнения в виде
, и записать общий интеграл этого уравнения в виде 
Теорема. Выражение P(x,y)dx+Q(x,y)dy есть полный дифференциал тогда и только тогда, когда выполнено равенство сигма P / сигма y =сигма Q / сигма x
7. Интегрирующий множитель. Достаточные условия существования интегрирующего множителя вида  (вывод).
(вывод).
8. Интегрирующий множитель. Достаточные условия существования интегрирующего множителя вида  (вывод).
(вывод).
Функция  называется интегрирующим множителем дифференциального уравнения (1), если после умножения (1) на
называется интегрирующим множителем дифференциального уравнения (1), если после умножения (1) на  получается уравнение
получается уравнение
 (2)
(2)
являющееся уравнением в полных дифференциалах.
Замечание 1. Умножение на функцию  и интегрирование вместо (1) уравнения (2) может привести к потере или появлению лишних решений, обращающих
и интегрирование вместо (1) уравнения (2) может привести к потере или появлению лишних решений, обращающих  в нуль.
в нуль.
Замечание 2. Дифференциальное уравнение (1) может иметь несколько интегрирующих множителей, а может не иметь ни одного.
Условия существования интегрирующего множителя
Интегрирующий множитель  удовлетворяет дифференциальному уравнению:
удовлетворяет дифференциальному уравнению:

Однако нет общего метода интегрирования такого уравнения. Рассмотрим частные случаи существования интегрирующих множителей вида:  и
и 
Теорема 1. Пусть в некоторой области D выполнены условия:
1)  непрерывны;
непрерывны;
2) 
3)  является функцией, зависящей только от переменной
является функцией, зависящей только от переменной 
Тогда дифференциальное уравнение (1) имеет интегрирующий множитель, зависящий только от 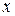 и вычисляемый по формуле:
и вычисляемый по формуле:

Теорема 2.Пусть в некоторой области D выполнены условия:
1)  непрерывны;
непрерывны;
2) 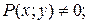
3) 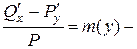 является функцией, зависящей только от переменной
является функцией, зависящей только от переменной 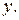
Тогда дифференциальное уравнение (1) имеет интегрирующий множитель, зависящий только от 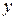 и вычисляемый по формуле:
и вычисляемый по формуле:

9. ДУ II-го порядка, допускающие понижение порядка.
Уравнения второго порядка, допускающие понижение порядка
1) Уравнение не содержит явно 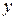 и
и 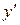
Пусть дифференциальное уравнение второго порядка имеет вид:
 (2)
(2)
Тогда, учитывая равенство:  получим:
получим:
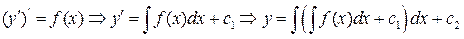
Следовательно, общее решение уравнения (2) задается функцией:

2) Уравнение не содержит явно 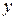
Пусть уравнение (1) имеет вид:
 (3)
(3)
Для решения такого уравнения выполняется замена:
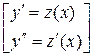
Эта замена понижает порядок уравнения, приводя уравнение (3) к ДУ первого порядка:
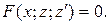
Решим полученное уравнение относительно функции  Получим общее решение этого уравнения:
Получим общее решение этого уравнения:
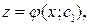
где 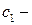 произвольная постоянная.
произвольная постоянная.
Далее, подставив в полученное решение 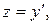 получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:

Откуда получим:
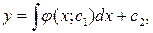
где  произвольная постоянная.
произвольная постоянная.
Итак, получено общее решение уравнения (3):

3) Уравнение не содержит явно 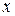
Пусть уравнение (1) имеет вид:
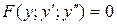 (4)
(4)
Для решения такого уравнения выполняется замена:

Эта замена понижает порядок уравнения, приводя уравнение (4) к ДУ первого порядка:
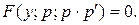
Решим полученное уравнение относительно функции 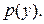 Получим общее решение этого уравнения:
Получим общее решение этого уравнения:
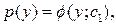
где 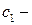 произвольная постоянная. Далее, подставив в полученное решение
произвольная постоянная. Далее, подставив в полученное решение  получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:

Это уравнение с разделяющимися переменными:

где  произвольная постоянная.
произвольная постоянная.
Итак, получим общий интеграл уравнения (4):

10. Свойства решений ЛДУ II-го порядка (с док-вом).
Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид: 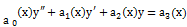 , (2.1)
, (2.1)
где  ,
, 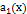 ,
,  и
и 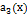 – заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a0(x) ≠ 0, поделим (2.1) на
– заданные функции, непрерывные на том промежутке, на котором ищется решение. Предполагая, что a0(x) ≠ 0, поделим (2.1) на  и, после введения новых обозначений для коэффициентов, запишем уравнение в виде:
и, после введения новых обозначений для коэффициентов, запишем уравнение в виде: 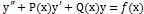 (2.2)
(2.2)
Примем без доказательства, что (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям 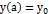 ,
, 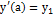 , если на рассматриваемом промежутке функции
, если на рассматриваемом промежутке функции 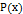 ,
,  и
и  непрерывны. Если
непрерывны. Если  , то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае. Рассмотрим свойства решений лоду 2-го порядка.
, то уравнение (2.2) называется однородным, и уравнение (2.2) называется неоднородным в противном случае. Рассмотрим свойства решений лоду 2-го порядка.
Определение. Линейной комбинацией функций 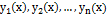 называется выражение
называется выражение 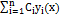 , где
, где  – произвольные числа.
– произвольные числа.
Теорема. Если  и
и 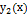 – решение лоду
– решение лоду 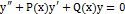 , (2.3) то их линейная комбинация
, (2.3) то их линейная комбинация 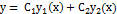 также будет решением этого уравнения.
также будет решением этого уравнения.
Доказательство.Поставим выражение 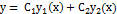 в (2.3) и покажем, что в результате получается тождество:
в (2.3) и покажем, что в результате получается тождество:
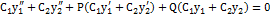 .
.
Перегруппируем слагаемые:  .
.
Поскольку функции  и
и 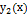 являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.
являются решениями уравнения (2.3), то каждая из скобок в последнем уравнении тождественно равна нулю, что и требовалось доказать.
Следствие 1. Из доказанной теоремы вытекает при 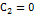 , что если
, что если  – решение уравнения (2.3), то
– решение уравнения (2.3), то 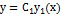 тоже есть решение этого уравнения. Следствие 2. Полагая
тоже есть решение этого уравнения. Следствие 2. Полагая 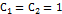 , видим, что сумма двух решений лоду
, видим, что сумма двух решений лоду 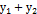 также является решением этого уравнения. Замечание. Доказанное в теореме свойство решений остается справедливым для лоду любого порядка.
также является решением этого уравнения. Замечание. Доказанное в теореме свойство решений остается справедливым для лоду любого порядка.
11. Линейная зависимость и независимость функций. Определитель Вронского. Фундаментальная система решений. ЛОДУ II-го порядка.


Фундаментальной системой решений линейного однородного дифференциального
уравнения n-го порядка называется любая линейно независимая система y1(x), y2(x),
…, yn(x) его n частных решений.
Теорема. Если 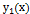 и
и 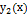 – линейно независимые решения уравнения (2.3), то их линейная комбинация
– линейно независимые решения уравнения (2.3), то их линейная комбинация  , где
, где  и
и  – произвольные постоянные, будет общим решением этого уравнения.
– произвольные постоянные, будет общим решением этого уравнения.
Доказательство. То, что  есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение
есть решение уравнения (2.3), следует из теоремы о свойствах решений лоду 2-го порядка. Надо только еще показать, что решение  будет общим, т.е. надо показать, что при любых начальных условиях
будет общим, т.е. надо показать, что при любых начальных условиях 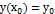 ,
,  можно выбрать произвольные постоянные
можно выбрать произвольные постоянные  и
и  так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:
так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде: 
Постоянные  и
и  из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы
из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы 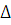 есть значение определителя Вронского для линейно независимых решений лоду при
есть значение определителя Вронского для линейно независимых решений лоду при 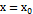 :
: 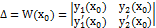 ,
,
а такой определитель, как мы видели в предыдущем параграфе, отличен от нуля. Теорема доказана.
12. Теорема о структуре общего решения ЛОДУ II-го порядка (с док-вом).
Общее решение ЛОДУ 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде 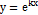 .
.
Подставляя эту функцию в уравнение (5.1), после сокращения на 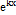 , получим алгебраическое уравнение, которое называется характеристическим:
, получим алгебраическое уравнение, которое называется характеристическим: 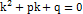 (5.2)
(5.2)
Функция 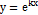 будет решением уравнения (5.1) только при тех значениях k, которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминанта
будет решением уравнения (5.1) только при тех значениях k, которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминанта 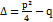 возможны три случая.
возможны три случая.
13. Построение общего решения ЛОДУ II-го порядка с постоянными коэффициентами в случае простых корней характеристического уравнения (случай D>0) (c док-вом).
1) 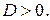 Тогда корни характеристического уравнения (4) действительные и различные –
Тогда корни характеристического уравнения (4) действительные и различные – 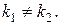 Они дадут два линейно независимых решения:
Они дадут два линейно независимых решения:  и
и  . Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
. Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:

14. Построение общего решения ЛОДУ II-го порядка с постоянными коэффициентами в случае кратных корней характеристического уравнения (случай D=0) (c док-вом).
2) 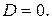 В этом случае
В этом случае 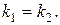 Поэтому одно решение уравнения (3) будет
Поэтому одно решение уравнения (3) будет  . В качестве второго, линейно независимого с первым, можно взять функцию
. В качестве второго, линейно независимого с первым, можно взять функцию  . Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
. Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:

или 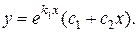
15. Построение общего решения ЛОДУ II-го порядка с постоянными коэффициентами в случае комплексно-сопряженных корней характеристического уравнения (случай D<0) (c док-вом).
3)  В этом случае корни уравнения (4) комплексно-сопряженные:
В этом случае корни уравнения (4) комплексно-сопряженные:  Тогда в качестве линейно независимых решений можно взять функции
Тогда в качестве линейно независимых решений можно взять функции  и
и  Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:

или 
16. Теорема о структуре общего решения ЛНДУ II-го порядка (с док-вом).
Теорема 1. Общее решение лнду 2-го порядка  f(x) (6.1)представляется в виде суммы общего решения
f(x) (6.1)представляется в виде суммы общего решения 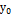 соответствующего однородного уравнения
соответствующего однородного уравнения  (6.2)и любого частного решения
(6.2)и любого частного решения 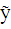 лнду (6.1).
лнду (6.1).
Доказательство.Докажем сначала, что  будет решением уравнения (6.1). Для этого подставим
будет решением уравнения (6.1). Для этого подставим  в уравнение (6.1):
в уравнение (6.1):  f(x). Это равенство является тождеством, т.к.
f(x). Это равенство является тождеством, т.к.  и
и 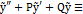 f(x). Следовательно,
f(x). Следовательно,  есть решение уравнения (6.1).
есть решение уравнения (6.1).
Докажем теперь, что это решение является общим, т.е. можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида: 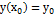 ,
, 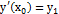 (6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде
(6.3). Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения (лоду) общее решение уравнения (6.2) можно представить в виде 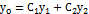 , где
, где 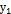 и
и  – линейно независимые решения этого уравнения. Таким образом:
– линейно независимые решения этого уравнения. Таким образом: 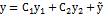 и, следовательно, начальные условия (6.3) можно записать в виде:
и, следовательно, начальные условия (6.3) можно записать в виде:  или
или  (6.4)
(6.4)
Произвольные постоянные  и
и  определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы
определяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, т.к. определитель этой системы 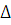 =
=  есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при
есть значение определителя Вронского для линейно независимых решений уравнения (6.2) при 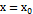 , а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные
, а такой определитель, как мы видели выше, отличен от нуля. Определив постоянные  и
и  из системы уравнений (6.4) и подставив их в выражение
из системы уравнений (6.4) и подставив их в выражение 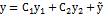 , мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
, мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.
17. Построение частного решения ЛНДУ II-го порядка в случае правой части вида 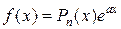 .
.
Пусть в уравнении (6.1) коэффициенты постоянны, т.е. уравнение имеет вид:  f(x) (7.1) где
f(x) (7.1) где  .
.
Рассмотрим метод отыскания частного решения 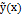 уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
уравнения (7.1) в случае, когда правая часть f(x) имеет специальный вид. Это метод называется методом неопределенных коэффициентов и состоит в подборе частного решения в зависимости от вида правой части f(x). Рассмотрим правые части следующего вида:
1. f(x)  , где
, где 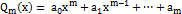 – многочлен степени
– многочлен степени  , причем некоторые коэффициенты, кроме
, причем некоторые коэффициенты, кроме 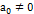 , могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
, могут равняться нулю. Укажем вид, в котором надо брать частное решение в этом случае.
а) Если число  не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде:
не является корнем характеристического уравнения для уравнения (5.1), то частное решение записываем в виде:  , где
, где  – неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
– неопределенные коэффициенты, которые подлежат определению методом неопределенных коэффициентов.
б) Если  является корнем кратности
является корнем кратности  соответствующего характеристического уравнения, то частное решение ищем в виде:
соответствующего характеристического уравнения, то частное решение ищем в виде:  , где
, где  – неопределенные коэффициенты.
– неопределенные коэффициенты.
18. Построение частного решения ЛНДУ II-го порядка в случае правой части вида 
f(x)  , где
, где  и
и  - многочлены степени
- многочлены степени 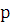 и
и  соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
соответственно, причем один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.
А) Если число 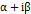 не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет:
не является корнем характеристического уравнения для уравнения (5.1), то вид частного решения будет:  , (7.2) где
, (7.2) где 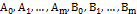 – неопределенные коэффициенты, а
– неопределенные коэффициенты, а 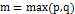 .
.
Б) Если число 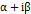 является корнем характеристического уравнения для уравнения (5.1) кратности
является корнем характеристического уравнения для уравнения (5.1) кратности  , то частное решение лнду будет иметь вид:
, то частное решение лнду будет иметь вид: 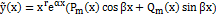 , (7.3) т.е. частное решение вида (7.2) надо умножить на
, (7.3) т.е. частное решение вида (7.2) надо умножить на  . В выражении (7.3)
. В выражении (7.3) 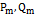 - многочлены с неопределенными коэффициентами, причем их степень
- многочлены с неопределенными коэффициентами, причем их степень 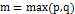 .
.
19. Метод вариации для решения ЛНДУ II-го порядка
Непосредственное нахождение частного решения лнду, кроме случая уравнения с постоянными коэффициентами, причем со специальными свободными членами, представляет большие трудности. Поэтому для нахождения общего решения лнду обычно применяют метод вариации произвольных постоянных, который всегда дает возможность найти общее решение лнду в квадратурах, если известна фундаментальная система решений соответствующего однородного уравнения. Этот метод состоит в следующем.
Согласно вышеизложенному, общее решение линейного однородного уравнения:
 , (8.1)
, (8.1)
где  – линейно независимые на некотором интервале X решения лоду, а
– линейно независимые на некотором интервале X решения лоду, а  - произвольные постоянные. Будем искать частное решение лнду в форме (8.1), считая, что
- произвольные постоянные. Будем искать частное решение лнду в форме (8.1), считая, что  – не постоянные, а некоторые, пока неизвестные, функции от
– не постоянные, а некоторые, пока неизвестные, функции от 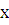 :
: 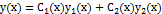 . (8.2) Продифференцируем равенство (8.2):
. (8.2) Продифференцируем равенство (8.2): 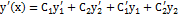 . (8.3)
. (8.3)
Подберем функции  и
и  так, чтобы выполнялось равенство:
так, чтобы выполнялось равенство:  . Тогда вместо (8.3) будем иметь:
. Тогда вместо (8.3) будем иметь:
 . (8.4)
. (8.4)
Продифференцируем это выражение еще раз по 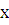 . В результате получим:
. В результате получим: 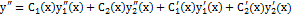 . (8.5) Подставим (8.2), (8.4), (8.5) в лнду 2-го порядка
. (8.5) Подставим (8.2), (8.4), (8.5) в лнду 2-го порядка  f(x):
f(x):
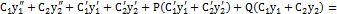 f(x)
f(x)
Или 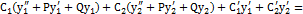 f(x). (8.6)
f(x). (8.6)
Так как  - решения лоду
- решения лоду  , то последнее равенство (8.6) принимает вид:
, то последнее равенство (8.6) принимает вид: 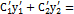 f(x).
f(x).
Таким образом, функция (8.2) будет решением лнду в том случае, если функции  и
и  удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
 (8.7)
(8.7)
Так как определителем этой системы является определитель Вронского для двух линейно независимых на X решений соответствующего лоду, то он не обращается в ноль ни в одной точке интервала X. Следовательно, решая систему (8.7), найдем 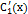 и
и 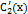 :
: 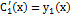 и
и  . Интегрируя, получи
. Интегрируя, получи  ,
,  , где
, где  – произв. пост.
– произв. пост.
Возвращаясь в равенство (8.2), получим общее решение неоднородного уравнения:  .
.
Ряды
1. Числовые ряды. Основные понятия, свойства сходящихся рядов. Необходимый признак сходимости (с док-вом).
Основные определения. Пусть дана бесконечная числовая последовательность 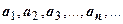 . Числовым рядом называется составленная из членов этой последовательности запись
. Числовым рядом называется составленная из членов этой последовательности запись  . Или
. Или 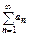 .Числа
.Числа 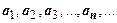 называют членами ряда;
называют членами ряда; 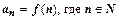 , называется общим членом ряда. В результате вычисления значений этой функции при n=1, n=2, n=3, … должны получаться члены ряда
, называется общим членом ряда. В результате вычисления значений этой функции при n=1, n=2, n=3, … должны получаться члены ряда  .
.
Пусть дан ряд (18.1.1). Составим из его членов конечные суммы, называемые частичными суммами ряда: 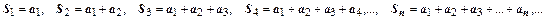
Определение. Если существует конечный предел S последовательности частичных сумм ряда (18.1.1) при  , то говорят, что ряд сходится; число S называют суммой ряда и пишут
, то говорят, что ряд сходится; число S называют суммой ряда и пишут  или
или  .
.
Если 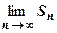 не существует (в том числе бесконечен), ряд называется расходящимся.
не существует (в том числе бесконечен), ряд называется расходящимся.
Свойства сходящихся рядов. Необходимый признак сходимости ряда. Общий член сходящегося ряда 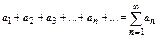 стремится к нулю при
стремится к нулю при  :
:  Доказательство. Если
Доказательство. Если 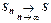 , то и
, то и  , но
, но 
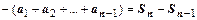 , следовательно
, следовательно  .
.
С проверки выполнения условия  надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2)
надо начинать решение любой задачи на исследование сходимости ряда: если это условие не выполняется, то ряд заведомо расходится. Это условие необходимо, но не достаточно для сходимости ряда: общий член гармонического ряда (18.1.2)  , однако этот ряд расходится.
, однако этот ряд расходится.
Определение. Остатком ряда после n-го члена называется ряд  .
.
Св-во 1. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
Доказательство. Пусть  - частичные суммы ряда (18.2.1); обозначим k-ую частичную сумму остатка
- частичные суммы ряда (18.2.1); обозначим k-ую частичную сумму остатка 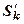 :
: 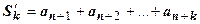 . Тогда
. Тогда 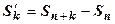 . Устремим
. Устремим 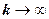 , считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный
, считая n фиксированным числом. Ряд (18.2.1) сходится, т.е. существует конечный 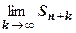 , следовательно существует конечный предел
, следовательно существует конечный предел  , т.е. остаток сходится. Обратное утверждение доказывается также. Так как
, т.е. остаток сходится. Обратное утверждение доказывается также. Так как 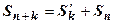 , то из существования конечного предела
, то из существования конечного предела  следует существование конечного предела
следует существование конечного предела 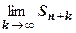 , т.е. из сходимости остатка следует сходимость ряда. Т.е. отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.
, т.е. из сходимости остатка следует сходимость ряда. Т.е. отбрасывание конечного числа начальных членов ряда или добавление в его начало нескольких новых членов не влияет на сходимость ряда.
Св-во 2. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при  .
.
Доказательство. Пусть S - сумма исходного ряда (18.2.1),  - сумма его остатка. Из равенства
- сумма его остатка. Из равенства 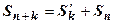 следует
следует  , т.е.
, т.е. 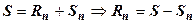 . Отсюда
. Отсюда  .
.
Из предыдущего свойства следует, что сходимость ряда определяется сходимостью его остатка, т.е. хвостом ряда, а сумма S ряда, как следует из равенства  , определяется пределом
, определяется пределом 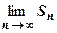 , т.е. началом ряда.
, т.е. началом ряда.
Св-во 3. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
Доказательство. Частичная сумма ряда 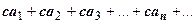 есть
есть  ; по свойству предела
; по свойству предела 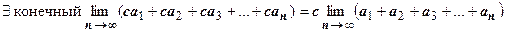 .
.
Св-во 4. Два сходящихся ряда  и
и 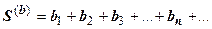 можно почленно складывать и вычитать; ряд
можно почленно складывать и вычитать; ряд  также сходится, и его сумма равна
также сходится, и его сумма равна 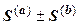 .
.
Доказательство и этого свойства - прямое следствие свойств пределов для частичных сумм:  .
.
2. Гармонический ряд. Ряды Дирихле.
Сходимость рядов с положительными членами (положительных рядов). Термином "положительный ряд" мы будем называть числовой ряд с неотрицательными членами:  для
для 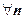 . Для таких рядов частичная сумма
. Для таких рядов частичная сумма 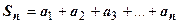 является возрастающей функцией аргумента n. Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху, поэтому сразу сформулируем признак сходимости положительных рядов:
является возрастающей функцией аргумента n. Монотонно возрастающая функция имеет конечный предел тогда и только тогда, когда она ограничена сверху, поэтому сразу сформулируем признак сходимости положительных рядов:
В случае, когда последовательность частичных сумм положительного ряда неограничена, будем говорить, что его сумма равна  .
.
При доказательстве расходимости гармонического ряда мы, по существу, доказали, что последовательность его частичных сумм неограничена. В качестве другого примера прямого применения этого признака рассмотрим ряд Дирихле (или обобщённый гармонический ряд)
 . (18.3.1)
. (18.3.1)
Если s<1, то  , и, так как частичные суммы
, и, так как частичные суммы  неограничены, то суммы
неограничены, то суммы  и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2:
и подавно неограничены, т.е. при s<1 ряд (18.3.1) расходится. Пусть теперь s>1. Как и для гармонического ряда сгруппируем члены в частичной сумме по степеням числа 2:  …+
…+  .Структура каждой скобки:
.Структура каждой скобки:  , поэтому
, поэтому  (мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
(мы воспользовались формулой для частичной суммы геометрической прогрессии). Последовательность ограничена; ряд сходится.
Итак, ряд Дирихле (18.3.1) сходится при s>1, расходится при s 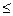 1.
1.
3. Признаки сравнения рядов с положительными членами (док-во 1-го и 2-го признаков).
Признак сравнения.Пусть даны два положительных ряда 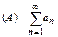 и
и 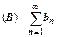 , для которых, хотя бы начиная с некоторого места (при n>N), выполняется неравенство
, для которых, хотя бы начиная с некоторого места (при n>N), выполняется неравенство 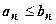 . Тогда: если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В). Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.
. Тогда: если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В). Другими словами, из сходимости большего ряда следует сходимость меньшего ряда, из расходимости меньшего ряда следует расходимость большего ряда. Сразу отметим, что из расходимости большего ряда, как и из сходимости меньшего ряда, никаких выводов о сходимости второго ряда сделать нельзя.
Доказательство этого утверждения непосредственно следует из сформулированного в начале раздела признака сходимости положительных рядов: если сходится больший ряд, то последовательность его частичных сумм ограничена, следовательно, ограничена последовательность частичных сумм меньшего ряда, следовательно, меньший ряд сходится; если расходится меньший ряд, то последовательность его частичных сумм неограничена, следовательно, неограничена последовательность частичных сумм большего ряда, следовательно, больший ряд расходится.
Предельная форма признака сравнения. Если существует конечный 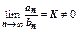 , то ряды (А) и (В) сходятся или расходятся одновременно.
, то ряды (А) и (В) сходятся или расходятся одновременно.
Доказательство. По определению предела для 
 . Последнего неравенства достаточно для доказательства всех утверждений теоремы.
. Последнего неравенства достаточно для доказательства всех утверждений теоремы. 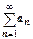 сходится
сходится  сх-ся
сх-ся 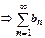 сх-ся. остальные случаи схематично: (А) расх-ся
сх-ся. остальные случаи схематично: (А) расх-ся 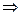 (3К/2 B) расх-ся
(3К/2 B) расх-ся  (B) расх-ся; (B) сх-ся
(B) расх-ся; (B) сх-ся  (3К/2 B) сх-ся
(3К/2 B) сх-ся  (A) сх-ся; (B) расх-ся
(A) сх-ся; (B) расх-ся  (К/2 B) расх-ся
(К/2 B) расх-ся 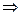 (A) расх-ся.
(A) расх-ся.
4. Признак Даламбера (с док-вом).
Пусть для положительного ряда существует 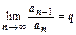 .
.
Тогда если q<1, то ряд сходится,
если q >1, то ряд расходится,
если q=1, то ряд может и сходиться, и расходиться.
Доказательство. 1. Пусть  <1. Возьмём
<1. Возьмём  .
.  . Если q<1, то число
. Если q<1, то число 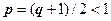 . Итак, при
. Итак, при 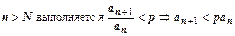 . Выпишем это неравенство для
. Выпишем это неравенство для  :
: 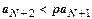 ,
, 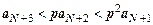 ,
,  , … ,
, … ,  . Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому
. Все члены ряда, начиная с N+2-го, меньше членов сходящейся геометрической прогрессии, поэтому 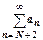 сходится, поэтому
сходится, поэтому 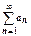 сходится.
сходится.
2. Пусть 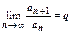 >1. Возьмём
>1. Возьмём 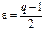 .
.  .
.
Если q>1, то число 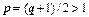 . Итак, при
. Итак, при 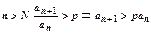 . Выпишем это неравенство для
. Выпишем это неравенство для  :
: 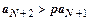 ,
, 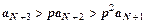 ,
, 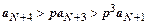 , … ,
, … ,  . Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому
. Все члены ряда, начиная с N+2-го, больше членов расходящейся геометрической прогрессии, поэтому 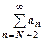 расходится, поэтому
расходится, поэтому  расходится.
расходится.
3. Для рядов  и
и  мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым. Признак Даламбера хорошо работает, если общий член ряда содержит факториалы.
мы опять получим q =1. Первый из этих рядов сходится, второй расходится, но для обоих q=1, т.е. в этом случае вопрос о сходимости ряда действительно остаётся открытым. Признак Даламбера хорошо работает, если общий член ряда содержит факториалы.
5. Интегральный признак Коши (с док-вом).
Радикальный признак Коши и признак Даламбера дают q =1 для рядов  и
и 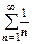 ,
, 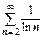 ,
,  и т.д. Для некоторых из этих рядов оказывается результативным интегральный признак Коши.
и т.д. Для некоторых из этих рядов оказывается результативным интегральный признак Коши.
Теорема.Пусть члены положительного числового ряда  являются значениями непрерывной монотонно убывающей неотрицательной функции
являются значениями непрерывной монотонно убывающей неотрицательной функции  при натуральных значениях аргумента:
при натуральных значениях аргумента: 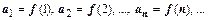 Тогда ряд
Тогда ряд  и несобственный интеграл
и несобственный интеграл 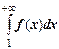 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Обозначим 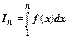 . Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой у=
. Согдасно геометрическому смыслу определённого интеграла, это площадь криволинейной трапеции под кривой у= 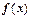 над отрезком [1,n]. Частичная сумма
над отрезком [1,n]. Частичная сумма 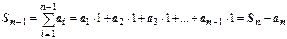 - площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма
- площадь ступенчатой фигуры, расположенной над криволинейной трапецией (сплошная верхняя граница на рисунке). Сумма  - площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно,
- площадь ступенчатой фигуры, расположенной под криволинейной трапецией (пунктирная верхняя граница на рисунке). Очевидно, 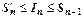 , или
, или  . Из этого неравенства, в котором
. Из этого неравенства, в котором  ,
, 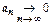 ,
, 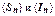 - монотонно возрастающие с ростом nпоследовательности, и следуют все утверждения теоремы. Например:
- монотонно возрастающие с ростом nпоследовательности, и следуют все утверждения теоремы. Например:
1. Пусть интеграл 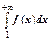 сходится. Это означает, что существует конечный
сходится. Это означает, что существует конечный  , т.е. последовательность
, т.е. последовательность 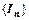 ограничена сверху
ограничена сверху 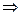 последовательность
последовательность 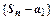 ограничена сверху
ограничена сверху 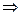 существует конечный
существует конечный  , т.е. ряд
, т.е. ряд  сходится.
сходится.
2. Пусть интеграл  расходится. Это означает, что
расходится. Это означает, что  бесконечен, т.е. последовательность
бесконечен, т.е. последовательность  неограничена сверху
неограничена сверху 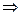 последовательность
последовательность 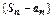 неограничена сверху
неограничена сверху 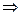 не существует конечного
не существует конечного  , т.е. ряд
, т.е. ряд 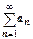 расходится.
расходится.
3, 4. Случаи, когда сходится и расходится ряд, рассмотреть самостоятельно.
Теперь мы можем дать простое доказательство того, что ряд Дирихле  сходится при s>1 и расходится в остальных случаях. Функция
сходится при s>1 и расходится в остальных случаях. Функция  удовлетворяет условиям теоремы: непрерывна, монотонно убывает,
удовлетворяет условиям теоремы: непрерывна, монотонно убывает,  . Интеграл
. Интеграл 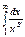 сходится, как мы знаем, при s>1 и расходится при других значениях s, что и требовалось доказать.
сходится, как мы знаем, при s>1 и расходится при других значениях s, что и требовалось доказать.
6. Знакочередующиеся ряды: признак Лейбница (с док-вом).
Ряд называется знакочередующимся, если любые два его соседних члена суть числа разных знаков. Несколько изменяя употреблявшуюся выше символику, будем обозначать через an не сам общий член ряда, а его абсолютную величину. Тогда, предполагая для определенности, что первый член знакочередующегося ряда положителен, мы сможем записать этот ряд в форме* a1 - a2 + a3 - a4 + a5 - ... (36)
 Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
Теорема Лейбница. Если абсолютная величина общего члена знакочередующегося ряда убывает и стремится к нулю, то этот ряд сходится.
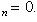 Действительно, допустим, что ряд (36) таков, что a1 > a2 > a3 > a4 > ..., (37) (38)
Действительно, допустим, что ряд (36) таков, что a1 > a2 > a3 > a4 > ..., (37) (38)
Образуем частичные суммы S2n: S2 = (a1 - a2), S4 = (a1 - a2) + (a3 - a4), S6 = (a1 - a2) + (a3 - a4) + (a5 - a6), . . . . . . .
Благодаря (37), все скобки положительны. Значит, S2 < S4 < S6 < ... Иначе говоря, последовательность {S2n} возрастает. С другой стороны, S2n = a1 - (a2 - a3) - (a4 - a5) - ... - (a2n-2 - a2n-1) - a2n, откуда ясно, что S2n < a1.
Как известно, при этих условиях существует конечный предел 
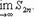 Но S2n+1 = S2n + a2n+1, откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к Sнезависимо от четности n. Иначе говоря,
Но S2n+1 = S2n + a2n+1, откуда в связи с (38) вытекает, что сумма S2n+1 с возрастанием n также стремится к S. Итак, при достаточно больших n сумма Sn будет сколь угодно близка к Sнезависимо от четности n. Иначе говоря, 
 чем и доказана теорема.
чем и доказана теорема.
7. Знакопеременные ряды: понятия абсолютной и условной сходимости, признак абсолютной сходимости, свойства абсолютно и условно сходящихся рядов.
Теперь рассмотрим такие ряды, знаки членов которых уже совершенно произвольны. При этом снова будем обозначать через a1, a2,a3 ... сами члены ряда.
Теорема 1. Сопоставим с рядом a1 + a2 + a3 + ... (39) ряд |a1| + |a2| + |a3| + ..., (40) составленный из абсолютных величин членов данного ряда. Если сходится ряд (40), то сходится и исходный ряд (39).
В самом деле, пусть ряд b1 + b2 + b3 + ... (41) есть ряд, состоящий из всех положительных (или равных нулю) членов нашего ряда (39) [причем их взаимное расположение таково же, как и в ряде (39)]. Пусть, далее, c1 + c2 + c3 + ... (42) есть ряд*абсолютных величин отрицательных членов ряда (39) (также расположенных в том порядке, в котором эти члены следуют друг за другом в исходном ряде).
Каждый из рядов (41) и (42) получается из сходящегося положительного ряда (40) путем вычеркивания части его членов (например, чтобы из (40) получить (41), надо вычеркнуть из (40) числа c1, c2, c3, ...). Поэтому в силу теоремы 4 ряды (41) и (42) сходятся. Обозначим их суммы соответственно через B и C.
Обозначим, далее, через An, Bn и Cn частичные суммы рядов (39), (41) и (42). Пусть среди чисел a1, a2, a3, ..., an имеется m(n) неотрицательных и p(n) отрицательных. Тогда An = Bm(n) - Cp(n). Правая часть этого равенства с ростом n стремится к разности B - C. Значит, и левая часть стремится к тому же пределу. Теорема доказана.
Заметим, что из сходимости ряда (39) не вытекает, что сходится (40). Например, ряд 
 сходится (это следует хотя бы из теоремы Лейбница), но ряд, составленный из абсолютных величин, будучи гармоническим, расходится. Таким образом, требование сходимости ряда (40) представляет собой более тяжелое требование, чем требование сходимости ряда (39). В связи с этим такой ряд (39), который не только сходится сам, но для которого и ряд абсолютных величин, называется абсолютно сходящимся. Если же ряд (39) сходится, но ряд (40) расходится, то говорят, что (39) есть ряд условно сходящийся.
сходится (это следует хотя бы из теоремы Лейбница), но ряд, составленный из абсолютных величин, будучи гармоническим, расходится. Таким образом, требование сходимости ряда (40) представляет собой более тяжелое требование, чем требование сходимости ряда (39). В связи с этим такой ряд (39), который не только сходится сам, но для которого и ряд абсолютных величин, называется абсолютно сходящимся. Если же ряд (39) сходится, но ряд (40) расходится, то говорят, что (39) есть ряд условно сходящийся.
Теорема 2. Если ряд (39) сходится абсолютно, то сходятся также ряды (41) и (42), образованные положительными членами и модулями отрицательных членов этого ряда. Суммы всех трех рядов связаны соотношением A = B - C. (43)
Признак сходимости Даламбера переносится в теорию рядов с членами любых знаков в следующей форме:
Теорема 3. Пусть ряд (39) таков, что существует предел 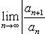
 Если l < 1, то ряд сходится, а если l > 1, то расходится.
Если l < 1, то ряд сходится, а если l > 1, то расходится.
Действительно, если l < 1, то по признаку Даламбера будет сходиться ряд абсолютных величин членов данного ряда, а значит, и подавно и сам ряд (39). Если же l > 1, то найдется такое m, что при n ≥ m будет 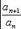
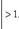
Но тогда |am| < |am+1| < |am+2| < ...,и общий член ряда (39) не стремится к нулю, откуда вытекает расходимость этого ряда.
Теорема 4. От перестановки членов абсолютно сходящегося ряда его абсолютная сходимость не нарушается и сумма не меняется.
Абсолютная сходимость ряда a1 + a2 + a3 + ... (49) означает сходимость положительного ряда |a1| + |a2| + |a3| + ... (50)
Пусть в результате перестановки своих членов ряд (49) превратится в ряд 
 (51)
(51)
Ясно, что ряд абсолютных величин членов ряда (51) получается некоторой перестановкой из ряда (50). Значит, этот ряд абсолютных величин сходится (по предыдущей теореме), а это и означает, что ряд (51) абсолютно сходится.
Введем, далее, ряды b1 + b2 + b3 + ..., (52) c1 + c2 + c3 + ..., (53) состоящие из неотрицательных и модулей отрицательных членов ряда (49). Эти ряды сходятся, и их суммы B и C связаны с суммой A ряда (49) формулой A = B - C. (54)
Когда производим перестановку членов в ряде (49), то это вызывает соответствующие перестановки в рядах (52) и (53), т. к. в этих рядах порядок членов такой же, как и в (49). Но так как ряды (52) и (53) - положительные, то их суммы B и C от перестановки не меняются. С другой стороны, сумма ряда (51) должна выражаться через суммы рядов, полученных упомянутыми перестановками из (52) и (53), той же формулой (54). Отсюда и видно, что сумма ряда (51) равна сумме ряда (49).
Условие абсолютной сходимости ряда для законности перестановок его членов не только достаточно, но и необходимо. Действительно, имеет место Теорема 5. Если ряд (49) сходится неабсолютно, то его члены можно переставить так, чтобы вновь полученный ряд имел любую наперед заданную сумму, а также так, чтобы он расходился.
Теорема 6. Если ряды (56) и (57) сходятся абсолютно и их суммы соответственно равны A и B, то и ряд (58) сходится абсолютно и сумма его C равна произведению сумм рядов (56) и (57) C = AB. (60) Иными словами, абсолютно сходящиеся ряды можно перемножать, как конечные суммы.
8. Степенные ряды: радиус, интервал, область сходимости. Свойства степенных рядов. Теорема Абеля (с док-вом).
Степенным рядом называется ряд вида c0 + c1x + c2x2 + c3x3 + ..., (1) где c0, c1, c2, ... - постоянные числа, называемые коэффициентами ряда. Про ряд (1) говорят, что он расположен по степеням x.
Лемма Абеля. Если степенной ряд (1) сходится при некотором значении x0 ≠ 0, то он абсолютно сходится при каждом x, у которого | x | < | x0 |. (6) В самом деле, так как общий член сходящегося ряда 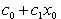


стремится к нулю с возрастанием своего номера, то 
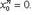 Но если какая-нибудь последовательность имеет предел, то множество членов этой последовательности ограничено. Поэтому существует такое число M, что
Но если какая-нибудь последовательность имеет предел, то множество членов этой последовательности ограничено. Поэтому существует такое число M, что 

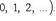 (7) Заметив это, рассмотрим ряд (1) при значении x, удовлетворяющем неравенству (6). Этот ряд можно переписать так:
(7) Заметив это, рассмотрим ряд (1) при значении x, удовлетворяющем неравенству (6). Этот ряд можно переписать так:
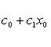
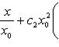
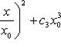
 (8)
(8)
В силу (7) ряд, состоящий из абс.величин членов последнего ряда, имеет мажорантный ряд 
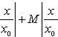

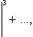
а так как этот ряд сходится (т. к. это есть геометрическая прогрессия со знаменателем  ), то ряд (8), или, что то же самое, ряд (1), сходится абсолютно. Лемма доказана/
), то ряд (8), или, что то же самое, ряд (1), сходится абсолютно. Лемма доказана/
Опр-е. 1) Степенной ряд сходится абсолютно на некотором интервале  . Иными словами, если мы выбираем любое значение «икс» из интервала
. Иными словами, если мы выбираем любое значение «икс» из интервала  и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал
и подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервал  и называется интервалом сходимости степенного ряда. Радиус сходимости, если совсем просто, это половина длины интервала сходимости:
и называется интервалом сходимости степенного ряда. Радиус сходимости, если совсем просто, это половина длины интервала сходимости: 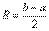
В точках  ,
,  степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
степенной рядможет, как сходиться, так и расходится, и для выяснения этого необходимо проводить дополнительное исследование. После такого исследования речь идёт уже об области сходимости ряда:
– Если установлено, что степенной ряд расходится на обоих концах интервала, то область сходимости ряда совпадает с интервалом сходимости: 
– Если установлено, что степенной ряд сходится на одном конце интервала и расходится на другом, то область сходимости рядапредставляет собой полуинтервал: 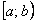 или
или  .
.
– Если установлено, что степенной ряд сходится на обоих концах интервала, то область сходимости ряда представляет собой отрезок: 
Термины очень похожи, область сходимости ряда – это чуть более детализированныйинтервал сходимости ряда.
2) Степенной ряд сходится абсолютно при любом значении  . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:
. То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получитсяабсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:  . Радиус сходимости:
. Радиус сходимости:  .
.
3) Степенной ряд сходится в единственной точке. Если ряд имеет вид  , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке  . В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:
. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:  . Если ряд имеет вид
. Если ряд имеет вид 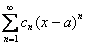 , то он будет сходиться в единственной точке
, то он будет сходиться в единственной точке  , если ряд имеет вид
, если ряд имеет вид  , то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:
, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:  .
.
Дата добавления: 2021-04-05; просмотров: 115; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
