Тема: Уравнение касательной в общем виде
Цель: формирование навыков составление уравнения касательной к графику функции
Методические указания.
Касательная к графику дифференцируемой в точке 
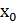функции f — это прямая, проходящая через точку ( 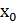, f( 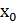)) и имеющая угловой коэффициент f '( )
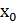Уравнение касательной к графику функции: y=f(x0)+f ¢(x0)(x-x0)
Алгоритм составления уравнения касательной:
1. Вычислить значение функции в точке касания f( )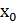
2. Найти производную функции f ¢(x)
3. Вычислить значение производной в точке касания f ¢( )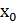
4. Подставить значения 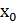, f( 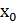), f ¢( 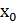) в уравнение касательной
у = f( 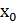)+f ¢( 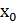)(x- )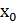
Пример1. (Если задана абсцисса точки касания)
Составить уравнение касательной к графику функции 
в точке М с абсциссой 
2.
Решение:
1. Вычислим значение функции: 
2. Найдём производную функции: 
3. Вычислим значение производной: 
4. Подставим эти значения в уравнение касательной:
у =-3+9(х-2) = -3 + 9х -18 =9х-21
Ответ: у =9х-21
Пример2. (Если задана ордината точки касания)
Составить уравнение касательной в точке графика 
с ординатой 
Решение:
1. Найдем абсциссу точки касания 
, 1-х = х +1, -2х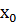=0, 
= 0
2. Найдем производную функции 
= 
= 
3. Найдем угловой коэффициент касательной k = 
: k = 
=-2
4. Запишем уравнение касательной: у = k(х- 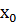)+b
y = -2 
(x -0) +1=-2x+1
Ответ: y = -2x+1
Пример 3. (Касательная заданного направления)
Составить уравнение касательной к графику функции у = - 
, параллельной прямой у = 2х +3
|
|
|
Решение:
1. Так как касательная параллельна прямой у = 2х +3, то они имеют один и тот же угловой коэффициент k = 2, k = 
= 
= -2х
2. Абсцисса 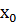точки касания удовлетворяет уравнению -2х = 2, значит 
3. Значение функции в точке касания у(-1) = - 
+ 1 = -1+1=0
4. 
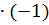-2 
=2
5. Составим уравнение касательной у = f( 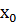)+f ¢( 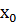)(x- )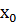
у=0+2(х+1) = 2х+1
Ответ: у=2х+1
Содержание работы
№1. Составить уравнение касательной к графику функции f в точке с абсциссой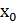
1. 
, 
2. 
, 
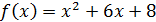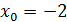
3. 
, 
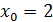
4. 
, 
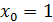
№2. Записать уравнение касательной к кривой в точке с ординатой 
1. 
, 
2. 
, 
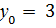
3. 
, 
4. 
, 
№3.
1. Записать уравнение касательной к графику функции 
, параллельной прямой у = 4х+3
2. Записать уравнение касательной к графику функции 
, параллельной прямой у = 1-х
№4.
1. Прямая у = 7х – 5 параллельна касательной к графику функции 
. Найдите точку касания
2. Прямая у = - 4х – 11 параллельна касательной к графику функции 
. Найдите точку касания
Контрольные вопросы
1. Что называется касательной к графику функции?
2. Формула уравнения касательной
3. Сформулировать алгоритм уравнения касательной
4. Условие параллельности двух прямых
Практическое занятие № 14
Тема: Правила дифференцирования, производные элементарных функций.
|
|
|
Цель: Формирование умений анализа условия задачи, применения знаний правил дифференцирования для решения задач.
Методические указания.
Правила дифференцирования. Производные элементарных функций
1. 
| 11. 
|
2. 
| 12. 
|
3. 
| 13. 
|
4. 
| 14. 
|
5. 
| 15. 
|
6. 
| 16. 
|
7. 
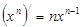
| 17. 
|
8. 
| 18. 
|
9. 
| 19. |
10. 
|
Найти производные следующих функций:
Пример 1
y=х2-4х+3.
Решение:
у / = (х2-4х+3) / = (х2)/ - (4х)/ + 3/.
По формулам 1,2, 3, 6 и 7 таблицы, получим у/ = 2х-4.
Пример 2
.
Решение:
Вводя дробные и отрицательные показатели, преобразуем данную функцию:
.
Применяя формулы (6 и 7), получим:
.
Пример 3
. Вычислить 
.
Решение:
По формулам (5 и 7) получим:
.
Пример 4
Решение:
Раскрываем скобки и производим деление:
.
Используем дробные и отрицательные показатели, приводя данное выражение к виду (7) таблицы 2.1:
.
Находим производную у /:
.
Пример 5
Найти производную 2-го порядка от функции 
.
Решение:
Используя формулы дифференцирования, получим:
.
Дифференцируя производную у /, имеем:
.
Пример 6
Движение летчика при катапультировании из реактивного самолета
можно приблизительно описать формулой 
(м). Определить скорость и ускорение летчика через 2 с после катапультирования.
|
|
|
Решение:
По формулам 3, 6,7 и 8 таблицы 2.1:
,
Тогда v=3,7•3t2 + 
м/с; 
.
Производная сложной функции
Если 
, где 
, т.е. если у зависит от х через промежуточный аргумент u, то у называется сложной функцией от х.
Производная сложной функции равна произведению ее производной по промежуточному аргументу на производную этого аргумента по независимой переменной: 
.
Найти производные следующих функций:
Пример 7.
.
Решение:
Полагая 1+5х = u и у = u3, применяя правило дифференцирования сложной функции, имеем:
.
Пример 8
.
Решение:
Полагая 3х= u, найдем, используя соответствующие формулы:
.
Пример 9
.
Решение:
Полагая х3= u, найдем:
.
Пример 10
В какой момент времени скорость тела, движущегося по закону 
, равна 0? Найти ускорение тела.
Решение:
Скорость тела v - это первая производная от перемещения 
по времени: 
; закону 
Если v=0, то 0=16t-15 
Ускорение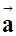 
– это первая производная от скорости 
по времени: 
; 
.
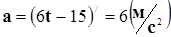Содержание работы
Найти производные функций при данном значении аргумента:
№ 1
1. 
2. 
3. 
(2)
4. 
5. 
( 
)
6. 
7. 
8. 
9. 
№ 2
1. 
2. 
3. 
4. 
5. 
6. 
7. 
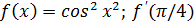
8. 
9. 
Контрольные вопросы
1.Запишите определение производной
|
|
|
2.Чем отличается производная сложной функции от производной элементарной функции?
Практическое занятие №15
Тема: Исследование функции с помощью производной.
Цель: ознакомление с понятиями монотонности функции, точками экстремума и экстремумами функции; формирование умения применять полученные знания для исследования функции.
Методические указания.
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Дата добавления: 2021-07-19; просмотров: 349; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!