Дифференциальные уравнения, допускающие понижение порядка.
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Часть А)
ЛИНЕЙНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА И УРАВНЕНИЕ БЕРНУЛЛИ
Линейные уравнения первого порядка. Решение типовых задач
Уравнение вида  называется линейным.
называется линейным.
Решение уравнение производится методом Бернулли. Представляем искомую функцию  через произведение двух функций
через произведение двух функций  , на одну из которых накладываем определённое условие.
, на одну из которых накладываем определённое условие.
20.1.1. Решить уравнение 
Решение. Перепишем уравнение в виде: 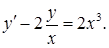 Сделаем замену
Сделаем замену  Подставив в уравнение, получим:
Подставив в уравнение, получим: 
 На переменную
На переменную  накладываем условие:
накладываем условие: 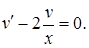 Разделяя переменные, имеем:
Разделяя переменные, имеем:  .
.
Тогда от решаемого уравнения останется  , откуда находим, что
, откуда находим, что  Окончательный ответ:
Окончательный ответ: 
Некоторые уравнения становятся линейными, если поменять местами искомую функцию и независимую переменную.
Например, уравнение 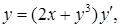 в котором
в котором  является функцией от
является функцией от  – нелинейное. Запишем его в дифференциалах:
– нелинейное. Запишем его в дифференциалах: 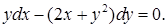 Так как в это уравнение
Так как в это уравнение  и
и 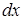 входят линейно, то уравнение будет линейным, если
входят линейно, то уравнение будет линейным, если  считать искомой функцией, а
считать искомой функцией, а  независимым переменным. Это уравнение может быть записано в виде
независимым переменным. Это уравнение может быть записано в виде  и решается аналогично уравнению 20.1.1.
и решается аналогично уравнению 20.1.1.
20.1.2. Решить уравнение 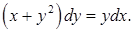
Решение. 



 ,
,  и
и  функции от переменной
функции от переменной  Имеем
Имеем

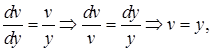

Ответ: 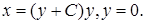
20.1.3. Решить уравнение 
Решение. Разделим уравнение на  :
:
 .
.
Это линейное уравнение относительно функции  .
.
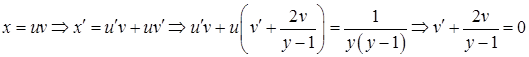 .
.
Откуда, получим  .
.
Тогда 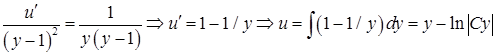 .
.
Откуда  .
.
При делении на  потеряны корни
потеряны корни  , которые не могут быть получены из общего решения ни при каких значениях
, которые не могут быть получены из общего решения ни при каких значениях  .
.
|
|
|
Ответ: 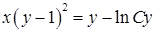 ,
,  .
.
Задачи для самостоятельного решения
20.2.1.  20.2.2.
20.2.2.  20.2.3.
20.2.3. 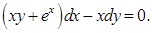 20.2.4.
20.2.4.  20.2.5.
20.2.5.  20.2.6.
20.2.6. 
Ответы. 20.2.1.  20.2.2.
20.2.2. 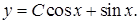 20.2.3.
20.2.3. 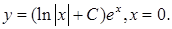 20.2.4.
20.2.4.  20.2.5.
20.2.5.  20.2.6.
20.2.6. 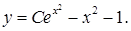
Уравнение Бернулли. Решение типовых задач
Чтобы решить уравнение Бернулли, которое имеет вид 
 , надо обе его части разделить на
, надо обе его части разделить на  и сделать замену
и сделать замену  После замены получается линейное уравнение, которое можно решить изложенным выше способом. Уравнение Бернулли можно также решать, как и линейное, заменой
После замены получается линейное уравнение, которое можно решить изложенным выше способом. Уравнение Бернулли можно также решать, как и линейное, заменой 
20.3.1. Решить уравнение 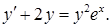
Решение. Разделим уравнение на  Получим
Получим  .
.
Далее произведём замену 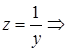
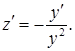
После замены получим линейное уравнение 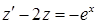 , решая которое получим:
, решая которое получим: 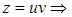
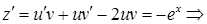



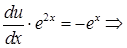
 Находим
Находим  . После обратной замены получим
. После обратной замены получим 
20.3.2. Решить уравнение 
Решение. Подставляя  в исходное уравнение, получим
в исходное уравнение, получим  или
или  .
.
Выберем в качестве  решение уравнения
решение уравнения 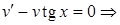
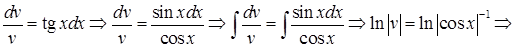
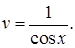 Тогда для
Тогда для  получим уравнение
получим уравнение 

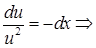
 . Общее решение уравнения исходного уравнения Бернулли равно
. Общее решение уравнения исходного уравнения Бернулли равно  .
.
Задачи для самостоятельного решения
Для части А)
Дистанционное обучение
20.4.1.  20.4.2.
20.4.2. 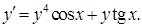 20.4.3.
20.4.3.  20.4.4.
20.4.4.  20.4.5.
20.4.5. 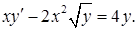 20.4.6.
20.4.6. 
Ответы. 20.4.1.  . 20.4.2.
. 20.4.2.  20.4.3.
20.4.3. 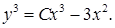 20.4.4.
20.4.4.  20.4.5.
20.4.5.  . 20.4.6.
. 20.4.6. 
|
|
|
ЧАСТЬ Б)
УРАВНЕНИЯ В ПОЛНЫХ ДИФФЕРЕНЦИАЛАХ.
УРАВНЕНИЯ, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА
Уравнения в полных дифференциалах. Решение типовых задач
Уравнение 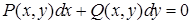 (1) называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции (1) называется уравнением в полных дифференциалах, если его левая часть является полным дифференциалом некоторой функции  , т.е. , т.е.  , что имеет место, если , что имеет место, если  В этом случае В этом случае  будет общим интегралом дифференциального уравнения (1).
Решение уравнения можно определить по формуле: будет общим интегралом дифференциального уравнения (1).
Решение уравнения можно определить по формуле: 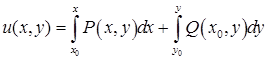 , где , где  произвольная точка области, в которой функции произвольная точка области, в которой функции  непрерывны. непрерывны.
|
21.1.1. Решить уравнение 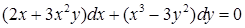
Решение. Так как  то исходное уравнение является уравнением в полных дифференциалах. Найдём функцию
то исходное уравнение является уравнением в полных дифференциалах. Найдём функцию  полный дифференциал которой
полный дифференциал которой  был бы равен левой части уравнения, т.е. такую функцию
был бы равен левой части уравнения, т.е. такую функцию 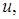 что
что 
Интегрируем по  первое из уравнений системы, считая
первое из уравнений системы, считая  постоянным; притом вместо постоянной интегрирования надо поставить
постоянным; притом вместо постоянной интегрирования надо поставить 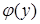 – неизвестную функцию от
– неизвестную функцию от  :
:  Подставляя это выражение для
Подставляя это выражение для  во второе уравнение системы, найдём
во второе уравнение системы, найдём 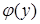 :
:

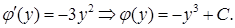
Следовательно, 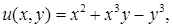 и общее решение исходного уравнения будет иметь вид
и общее решение исходного уравнения будет иметь вид 
Иногда можно найти такую функцию  , что
, что  будет полным дифференциалом, хотя
будет полным дифференциалом, хотя  может им не быть.
может им не быть.
|
|
|
Такую функцию  называют интегрирующим множителем.
называют интегрирующим множителем.
Функция  удовлетворяет условию
удовлетворяет условию 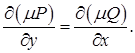
Интегрирующий множитель легко находится в двух случаях:
1)  , тогда
, тогда  ;
;
2)  , тогда
, тогда  .
.
21.1.2. Решить уравнение  .
.
Решение. Здесь 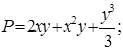
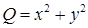 ,
,  , следовательно,
, следовательно,  . Так как
. Так как  , то в этом случае
, то в этом случае  , или
, или 

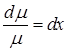 , откуда
, откуда  . Умножив уравнение на
. Умножив уравнение на 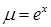 , получим уравнение в полных дифференциалах
, получим уравнение в полных дифференциалах  , общий интеграл которого имеет вид
, общий интеграл которого имеет вид  .
.
21.1.3. Решить уравнение  , если
, если  .
.
Решение. Здесь 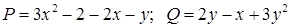 ;
;  .
.
Имеем уравнение в полных дифференциалах. Воспользуемся формулой для общего решения  , если
, если  .
.

 где
где  .
.
Решение уравнения имеет вид 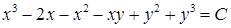 .
.
Дифференциальные уравнения, допускающие понижение порядка.
Решение типовых задач
Дифференциальное уравнение  го порядка имеет вид
го порядка имеет вид 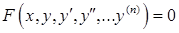 .
.
Если это уравнение решить относительно  то оно может быть представлено в виде
то оно может быть представлено в виде 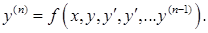
Определение. Решением ДУ на интервале  называется всякая функция
называется всякая функция  , зависящая от
, зависящая от  произвольных постоянных
произвольных постоянных  и такая, что подстановка
и такая, что подстановка 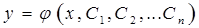 и ее производных в дифференциальное уравнение обращает последнее на интервале
и ее производных в дифференциальное уравнение обращает последнее на интервале  в тождество по
в тождество по  .
.
Задача Коши: задача отыскания решения  дифференциального уравнения, удовлетворяющего заданным начальным условиям
дифференциального уравнения, удовлетворяющего заданным начальным условиям  ,
, 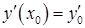 , ………….
, …………. 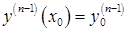 .
.
|
|
|
Теорема. Если функция  непрерывна по совокупности аргументов, имеет непрерывные производные
непрерывна по совокупности аргументов, имеет непрерывные производные 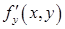 ,
,  ,
,  , …,
, …,  в некоторой области, содержащей точку
в некоторой области, содержащей точку 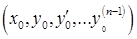 , то существует и притом единственное решение задачи Коши.
, то существует и притом единственное решение задачи Коши.
Определение. Пусть выполняются условия предыдущей теоремы.
Общим решением дифференциального уравнения  в некоторой области
в некоторой области  существования и единственности решения задачи Коши называется функция
существования и единственности решения задачи Коши называется функция  , зависящая от переменной
, зависящая от переменной  и
и  постоянных
постоянных  , такая, что:
, такая, что:
а) при любых допустимых значениях постоянных  функция
функция  является решением уравнения;
является решением уравнения;
б) при заданных начальных условиях постоянные  всегда можно подобрать так, что функция
всегда можно подобрать так, что функция  будет удовлетворять этим условиям.
будет удовлетворять этим условиям.
В процессе интегрирования дифференциального уравнения часто приходят к уравнению 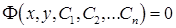 , неявно задающему общее решение уравнения. Уравнение
, неявно задающему общее решение уравнения. Уравнение 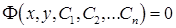 называется общим интегралом дифференциального уравнения.
называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения называется решение, получаемое из общего решения при конкретных значениях произвольных постоянных  .
.
Уравнение  , где
, где  некоторые значения постоянных
некоторые значения постоянных  называется частным интегралом дифференциального уравнения.
называется частным интегралом дифференциального уравнения.
21.2.1. Уравнение вида  Решение типовой задачи
Решение типовой задачи
21.2.1.1. Найти общее решение уравнения  .
.
Решение. Этот вид уравнений решается последовательным интегрированием:

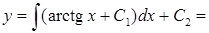
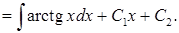 Интегрируя по частям, находим общий интеграл:
Интегрируя по частям, находим общий интеграл: 
21.2.2. Уравнение не содержит переменной  в явном виде. Решение типовых задач
в явном виде. Решение типовых задач
Уравнение вида  Понижение порядка ДУ производится путем замены
Понижение порядка ДУ производится путем замены  .
.
21.2.2.1. Решить уравнение 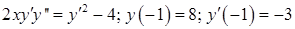 .
.
Решение. В уравнении отсутствует неизвестная функция  , поэтому порядок уравнения можно понизить путем замены
, поэтому порядок уравнения можно понизить путем замены  , где
, где  – новая неизвестная функция. Тогда
– новая неизвестная функция. Тогда  и уравнение примет вид
и уравнение примет вид 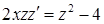 . Это уравнение с разделяющимися переменными:
. Это уравнение с разделяющимися переменными:

 .
.
Таким образом,  . Подставляя сюда
. Подставляя сюда 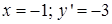 , имеем:
, имеем:  . Значит, знак перед корнем должен быть «–», и
. Значит, знак перед корнем должен быть «–», и  . Интегрируем по
. Интегрируем по 
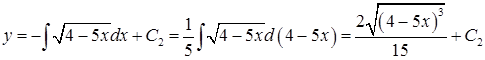 .
.
Подставим в это равенство  :
:
 – искомое частное решение.
– искомое частное решение.
21.2.2.2. Решить уравнение  ;
;  ,
,  .
.
Решение. Сделаем замену  . Тогда
. Тогда

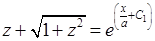 . Подставляя начальное условие
. Подставляя начальное условие 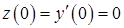 , получим
, получим
 . Тогда
. Тогда  . Интегрируя уравнение по переменной
. Интегрируя уравнение по переменной  , запишем
, запишем 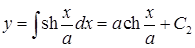 . С учетом начального условия
. С учетом начального условия  , определяем
, определяем  :
:  . Получим частное решение:
. Получим частное решение: 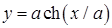 .
.
21.2.2.3. Найти общее решение уравнения 
Решение. Делаем подстановку 
 или
или  получено линейное уравнение первого порядка. Полагая
получено линейное уравнение первого порядка. Полагая  найдём:
найдём: 


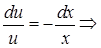

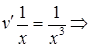




 или окончательно
или окончательно 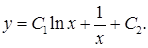
Дата добавления: 2021-07-19; просмотров: 79; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
