Миноры и алгебраические дополнения.
Понятие матрицы. Типы матриц (с примерами).
Матрица — математический объект, записываемый в виде прямоугольной таблицы элементов (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы.
Желтым выделены строки (обозначаются буквой m), а фиолетовым выделены столбцы (обозначаются буквой n). На пересечении них находится элемент матрицы под номером строки 1 и столбца 1, то есть а11, равный 3.
Типы матриц:
Прямоугольная:
Квадратная (частный случай прямоугольной):
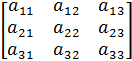
Как можно заметить, число столбцов n и число строк m равны. Данная матрица – 3го порядка. У квадратной матрицы также есть диагонали – главная (a11, a22, a33) и побочная (a31, a22, a13).
Вектор – строка:
Вектор строка есть матрица размером m строк и n = 1
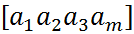
Вектор – столбец:
Вектор столбец есть матрица размером n столбов, и m = 1
Линейные операции над матрицами.
Алгебраическое сложение (оно же сложение и вычитание матриц)
Свойства сложения:
1. Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А + (В + С) = (А + В) + С.
2. Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А + 0 =А.
3. Для ненулевой матрицы А данного порядка существует матрица (–А), их суммой является нулевая матрица: А + (-А) = 0.
|
|
|
4. Для матриц А и В данного порядка справедливо свойство коммутативности сложения: А + В = В + А.
Произведение/деление на число отличное от нуля (в случае умножения на 0, получается так называемая нулевая матрица).
Свойства сложения:
1. Для матриц одного порядка А и В, а также произвольного действительного (или комплексного) числа 
справедливо свойство дистрибутивности умножения относительно сложения 
.
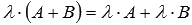2. Для произвольной матрицы А и любых действительных (или комплексных) чисел и 
выполняется свойство дистрибутивности 
.
3. Для произвольной матрицы А и любых действительных (или комплексных) чисел и справедливо свойство ассоциативности умножения 
.
4. Нейтральным числом по умножению на произвольную матрицу А является единица, то есть,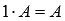 
.
Примеры:
Сложение/вычитание:
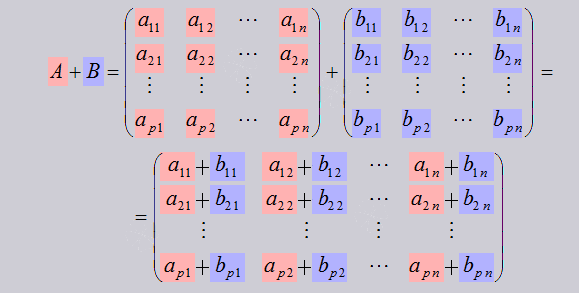
Умножение на число:
23. Произведение матриц.
Бля хз как это нормально объяснить
Транспонированная и обратная матрица.
Транспонированная матрица — матрица 
{\displaystyle A^{T}}, полученная из исходной матрицы А {\displaystyle A}заменой строк на столбцы.
То есть, если у нас была матрица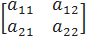 
то станет 
Свойства транспонированных матриц:
1) Дважды транспонированная матрица А равна исходной матрице А.
|
|
|
2) {\displaystyle (A^{T})^{T}=A}Транспонированная сумма матриц равна сумме транспонированных матриц.
3) {\displaystyle (A+B)^{T}=A^{T}+B^{T}}Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
4) {\displaystyle (AB)^{T}=B^{T}A^{T}}При транспонировании можно выносить скаляр.
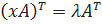
5) {\displaystyle (\lambda A)^{T}=\lambda A^{T}}Определитель транспонированной матрицы равен определителю исходной матрицы.
Миноры и алгебраические дополнения.
26. Ранг матрицы.
Дата добавления: 2021-07-19; просмотров: 51; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!