Центральное поле. Разделение переменных.
Момент импульса.
Полезно рассмотреть оператор момента импульса L, определяемый формулой:

Векторное произведение раскрывается в виде матрицы:
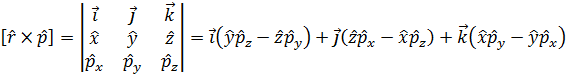
Таким образом компоненты момента импульса системы есть:



Момент импульса отдельной частицы, однако, условимся измерять в единицах ħ, то есть:


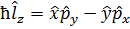
Вычислим для них пару полезных коммутаторов:

Также
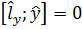

В общем виде:


Аналогично:

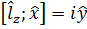
Все соотношения можно записать через символ Леви-Чивитты:

Где:

Найдём коммутатор:

Значит:
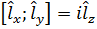
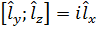

Или

Можно составить оператор:

Этот оператор коммутирует с каждой из компонент. Например найдём коммутатор:
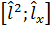



Сложив все равенства получим, что

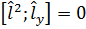

Полезно также ввести операторы l+ и l-:

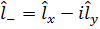
Для них имеем коммутационные соотношения:

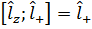

А также

Выразим оператор Лапласа в сферических координатах. Для этого выпишем преобразования из декартовых координат в сферические:
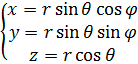
Распишем производную некоторой функции по радиусу:

По φ имеем:

И, наконец, по θ:

Далее же будем опускать f, рассматривая только операторы производных. Имеем тогда систему:

Частные производные от координат посчитать легко:



В итоге получим:

Решим систему методом Крамера:



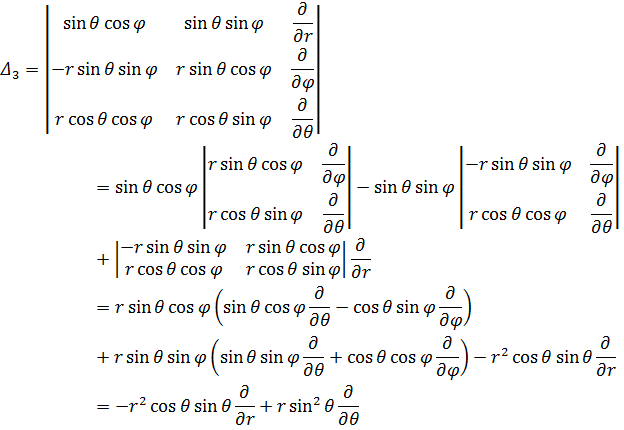



Выпишем оператор набла:
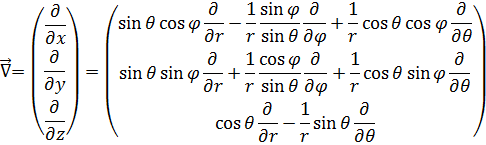
Тогда оператор Лапласа:

Где мы выделили радиальный оператор Лапласа:

И угловой:
|
|
|

Выпишем компоненты момента импульса в сферических координатах. Для этого заметим, что:

Значит:
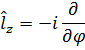
Умножим теперь третье равенство на sinθsinφ, а второе на cosθcosφ:
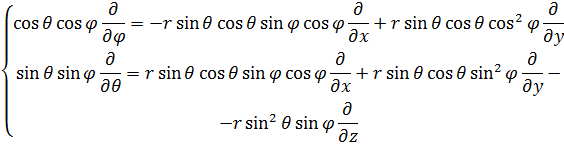
Сложим их и поделим на sinθ:

Теперь домножим на cosθsinφ и sinθcosφ, вычтем и поделим на sinθ




С помощью полученных выражений можно найти оператор квадрата момента импульса:

А квадрат полного момента импульса:


Задачи на собственные функции.
Займёмся теперь исследованием данных операторов на собственные числа и собственные функции. Наиболее простое уравнение возникает для lz, поэтому начнём с него:

Что эквивалентно дифференциальному уравнению:

Представим волновую функцию ψ как произведение функции от r и θ на функцию от φ:

Подставив в уравнение, получим:

Для краткости аргументы в вычислениях условимся опускать. Поделив обе части на f(r,θ) приходим к уравнению:
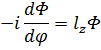
Разделим переменные и возьмём интегралы:


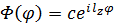
На данную функцию накладывается условие периодичности, ведь поворот на 2π не приведёт в ту же точку, а значит волновая функция не должна измениться:

Представим экспоненту в виде синуса и косинуса:
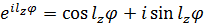
Условие периодичности накладывает 2 эквивалентных условия:
|
|
|
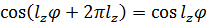

Распишем косинус суммы:
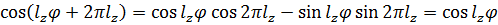
Для выполнения данного равенства надо потребовать одновременного выполнения двух условий:

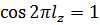
Откуда:
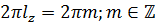

Значит

Нормируем данные волновые функции. Т.к. на повороты не накладывается ограничения, нормировать требуется на δ-функцию:



Найдём теперь собственные числа квадрата момента импульса. Вообще говоря требуется решить задачу на нахождение собственных функций оператор L2:

Или дифференциальное уравнение:

Однако для отыскания собственных чисел можно воспользоваться только коммутационными соотношениями, оставив задачу на собственные функции на потом. Пусть ψm – волновые функции, относящиеся к одному вырожденному уровню энергии. Заметим, что

Откуда следует:

Или же

Это значит, что все возможные значения lz при данном l2 ограничены. Переобозначим |lz|, соответствующий максимальному значению, просто через l. Т.е. l=max{|lz|}. Применим операторы lzl+ и lzl- к функции ψm:

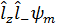
Применив коммутационные соотношения, получим:


А значит:

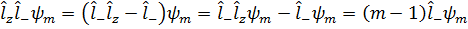
Или же:

Значит l±ψm есть собственная функция для lz, а значит можно написать:


Видно, что данные операторы аналогичны операторам рождения и уничтожения. Рассмотрим состояние при максимальном m, то есть при m=l. Т.к. это последнее существующее состояние, должно выполняться равенство:
|
|
|

Ибо состояние с m>l нет по определению. Можем тогда рассмотреть действие оператора l-l+:

Раскрыв скобки, получим:

Откуда:


Тогда модуль полного момента импульса в состоянии ψl есть

Центральное поле. Разделение переменных.
В атоме водорода присутствует протон и электрон, поэтому мы имеем задачу о двух телах. Гамильтониан такой системы есть сумма гамильтониана электрона и гамильтониана протона. Условимся обозначать величины, относящиеся к ядру большими буквами или греческими индексами, а всё, относящиеся к электрону, строчными буквами. Тогда имеем гамильтониан для водородоподобного атома в виде:
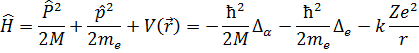
В классической механике такая задача может быть сведена к задаче одного тела путём помещения начала координат в центр масс. Введём радиус-вектор центра масс:

А также вектор взаимного расположения ядра и электрона:

При помещении системы координат в центр масс R=0, тогда из уравнений


Можно выразить re и rα:

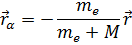
Также требуется пересчитать частные производные по координатам X, Y, Z центра масс и координатам x, y, z вектора взаимного расположения:
|
|
|

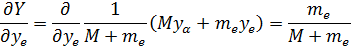




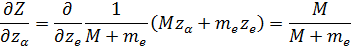
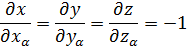



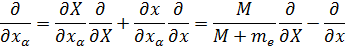

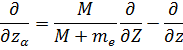
Тогда при переходе к оператору Гамильтона получим:

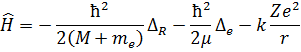

Есть приведённая масса электрона. Теперь же можно записать стационарное уравнение Шрёдингера:

Представим волновую функцию как произведение волновых функций, одна из которых отвечает за движение атома как целого, а вторая за движение электрона:

Тогда:

Разделим на ψRψе:

Переменные разделились, и мы видим, что


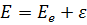

Первое уравнение есть уравнение свободной частицы массы M+me, то есть атома как целого. Оно легко решается и описывается обыкновенной волной де-Бройля. Второе уравнение есть уравнение движения электрона вокруг ядра, для которого оператор Лапласа записывается в сферических координатах и для которого нам предстоит решать уравнение Шрёдингера. Мы не будем интересоваться свободным движением, поэтому впредь условимся электронный оператор Лапласа, энергию электрона в атоме и его волновую функцию обозначать без индекса е, подразумевая заранее, что речь идёт только про электрон.
Классический анализ.
На самом деле выражение для гамильтониана системы можно получить практически сразу, опираясь только лишь на классические соображения. Действительно, напишем выражение для полной энергии:

В свою очередь скорость можно разделить на радиальную составляющую и перпендикулярную:

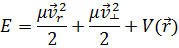
В свою очередь момент импульса есть:
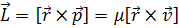


Значит функция Гамильтона есть:
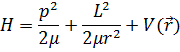
А оператор Гамильтона:

Величина
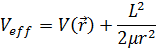
Называется эффективным потенциалом

Рис. 1 «Зависимость эффективного потенциала от расстояния»
Перейдём теперь к квантовому рассмотрению данной задачи.
Разделение переменных.
Запишем уравнение Шрёдингера для электрона:

Подставим оператор Лапласа в сферических координатах:
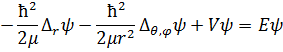
Можно заметить, что оператор
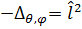
Поэтому:
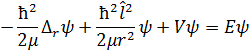
Представим волновую функцию как произведение двух функций, одна из которых зависит только от радиуса, а вторая только от углов:
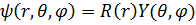
Тогда:

Учитывая тот приятный факт, что мы знаем собственные числа оператора квадрата момента импульса, можно переписать уравнение, разделив переменные:

Мы получили радиальное и угловое уравнения. Угловое уравнение в свою очередь разделяется ещё на 2:

Подставим угловую часть оператора Лапласа:

Представим угловую функцию как произведение функций, одна из которых зависит только от θ, а вторая только от φ:

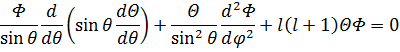
Разделим на ΘΦ:

Воспользуемся тем фактом, что мы знаем собственные числа оператора lz и, соответственно, lz2:


В итоге всего мы получаем 3 уравнения:

Решения последнего уравнения мы знаем, займёмся теперь первым угловым уравнением. Уравнение
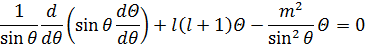
Называется присоединённым уравнением Лежандра. У данного уравнения существуют особенности, т.к. sinθ обращается в 0 в точках 0 и 2π, поэтому требуется потребовать ограниченности решения в этих точках. Но перед этим произведём замену переменных:


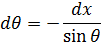

Перед анализом присоединённого уравнения Лежандра проанализируем уравнение Лежандра:

Поищем решение данного уравнения в виде ряда:
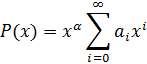
Пересчитаем производную:

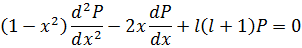



Перенумеруем члены: формально произведём замену i:=i+2, где в степени присутствует i-2:

Запишем всё под одну сумму:

Для того, чтобы данное уравнение обращалось в 0, надо потребовать обращение в 0 всех коэффициентов, получив рекуррентное соотношение:
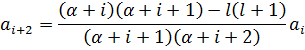
Положим a0=0, а а1=1. α же, как оказывается, можно выбрать равной 0 (тогда будут содержаться только чётные степени x) или 1 (тогда нечётные). Также в силу требования ограниченности надо потребовать, чтобы ряд обрывался. Для этого при некотором значении l числитель должен обращаться в 0:

Вычислим первые полиномы:

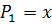



Полиномы Лежандра представляются весьма удобной формулой Родрига:
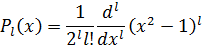
Присоединённые полиномы Лежандра выражаются через полиномы Лежандра:
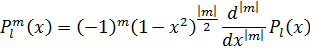
А значит нормированные волновые функции есть:

(Мы не будем подробно вдаваться в нормирование полиномов Лежандра, а примем как данность).
Решим теперь радиальное уравнение:

Произведём подстановку


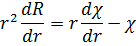

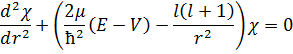
При этом на функцию χ(r) наложено ограничение χ(0)=0. Важно понять, как ведёт себя радиальная функция вблизи начала координат. Можно представить радиальную функцию в виде ряда и, в силу того, что r→0, оставить только постоянный член. При этом будем считать, что в начале координат выполняется
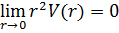
Если мы домножим радиальное уравнение на r2 и применим данное требование, то получим:
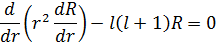
Подставим R в виде:




Или же

Откуда получаем 2 решения:

При s=-(l+1) решение в 0 обращается в бесконечность, поэтому требуется оставить только s=l. Итак, в начале координат радиальная функция ведёт себя как:

Мы знаем, что в атоме водорода между протоном и электроном действует кулоновское поле, поэтому требуется решить уравнение Шрёдингера для конкретного вида потенциала:

Для такого потенциала радиальное уравнение имеет вид:
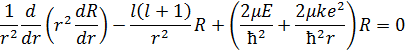
Удобно перейти в атомную систему единиц, в которой расстояния меряются в радиусах атома водорода:
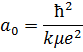
Будем измерять длину в радиусах атома водорода, а энергию в единицах энергии уровней атома водорода. Тогда уравнение перепишется в виде:

Введём новые переменные:


Величина под корнем положительна, ибо мы рассматриваем связные состояния (E<0). Произведём данную подстановку



Рассмотрим решение при больших ρ. Тогда членами, содержащими 1/ρ и 1/ρ2 можно пренебречь, оставив только:

Экспоненциальной подстановкой можно найти решение этого уравнения:

Значит решение можно искать в виде:
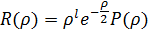
Подставив это решение в уравнение, придём к уравнению для Р:

Которое по своей форме напоминает уравнение, определяющее обобщённые полиномы Лагерра:


Таким образом радиальная функция есть:

К этим же результатам можно прийти, действуя более прямым методом.
Наложим требование ограниченности радиальной функции на бесконечности и поищем её в виде:

Где функция f(r) возрастает:


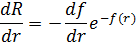
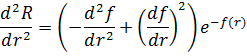

Сократим на экспоненту:

Рассмотрим поведение уравнения на бесконечности. Пренебрежём членами, содержащими 1/r, а так же второй производной, ибо она растёт куда медленнее первой:
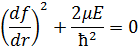
Мы получили интересный результат. Чтобы решение было вещественным, требуется, чтобы энергия была отрицательной. Этого, вообще говоря, следовало ожидать, ибо финитное движение в центральном поле возможно только при отрицательной энергии. Будем теперь писать вместо E -|E|. Отсюда:

Т.к. функция должна возрастать, выберем решение с +:

Константу интегрирования положим равной 0. Тогда
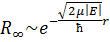
Решение в основной области поищем в виде произведения асимптотического решения на некоторый полином:
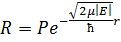



Сократим на экспоненту и приведём подобные:
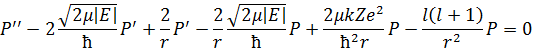
Подставим полином и его производные:
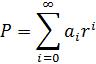



Сделаем перенумеровку:
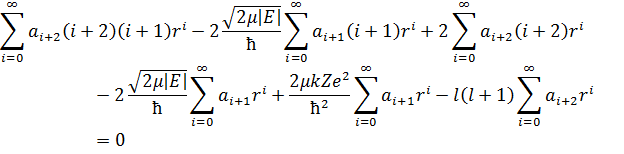
Запишем всё в одну сумму:

Получаем рекуррентное соотношение:

Полученное соотношение неограниченно возрастает на бесконечности, поэтому потребуем обрыва ряда обращением числителя в 0 при некотором i (также переобозначим i+2=n):

Откуда:

Дальнейшее решение уже было получено. Запишем тогда радиальную функцию сразу с нормировкой:

Где введено обозначение:

Здесь был решён более общий случай водородоподобного атома
Таким образом выходит, что электрон в атоме водорода описывается 3-мя числами: n, l и m, которые называются квантовыми числами. Число n называют главным квантовым числом, оно определяет энергетический уровень, на котором находится электрон. Состояния, определяющиеся разными числами l могут находиться при одной и той же энергии. Получается, что энергетические уровни вырождены, причём это вырождение 2l+1-кратно. l называют орбитальным квантовым числом, оно определяет форму орбитали и, соответственно, импульс электрона. m называют магнитным квантовым числом. Мы указывали, что l=max{|lz|}=max{|m|}, а значит m пробегает значения от –l до l и всего их будет 2l+1. Для l в химии принято буквенные обозначения, приведённые в таблице 1:
| l | 0 | 1 | 2 | 3 | 4 |
| В буквах | s | p | d | f | g |
Магнитное квантовое число определяет ориентацию орбитали в пространстве. Выпишем волновые функции некоторых состояний:

Для состояния (1,0,0) характерна независимость функции от углов. Вообще говоря, такая независимость характерна для любого состояния (n,0,0), из чего можно сделать вывод, что все s-орбитали для любого уровня сферически симметричны:

Рис. 2. «s-орбиталь»
Теперь рассмотрим уровень n=2. Там будут существовать 4 функции: (2,0,0), (2,1,0), (2,1,-1) и (2,1,1):


График вида f=r*sinθ есть окружность, пересекающая начало координат. Если мы провернём этот график на 2π, то получим 2 соприкосающиеся окружности:
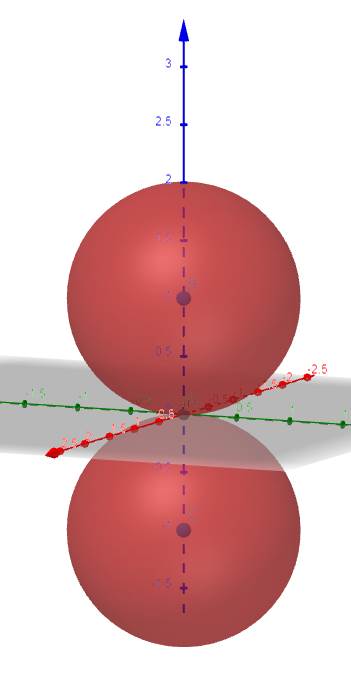
Рис. 3. «p-орбиталь»
Различные значения m определяют ориентацию данной системы в пространстве – либо вдоль оси z, либо вдоль x, либо вдоль y. Это так называемые p-орбитали.
Теперь n=3, помимо (3,0,0), (3,1,-1), (3,1,0) и (3,1,1) там появятся состояния (3,2,-2), (3,2,-1), (3,2,0), (3,2,1) и (3,2,2). Выпишим только функции d-орбиталей:

Данные орбитали имеют весьма сложную форму. Рисунки орбиталей приведены на рис. 4:

Рис. 4. «Орбитали»
Рассмотрим теперь поведение радиальной функции. Для s-стояний она будет выглядеть так:

Рис. 5. «R(r) для 1s состояния (r измеряется в единицах a0)»
Плотность вероятности обнаружения находится как:

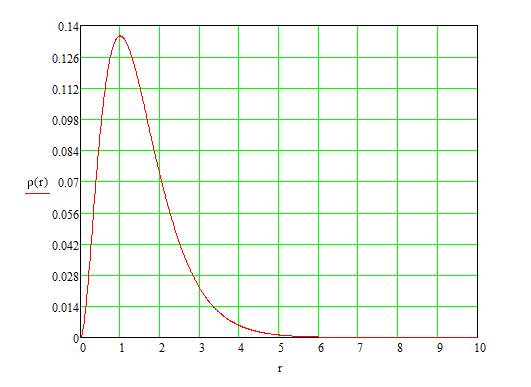
Рис. 6. «ρ(r) для 1s состояния (r измеряется в единицах a0)»
Видно, что для 1s состояния максимум плотности вероятности приходится на расстояние r=a0, то есть обнаружить электрон вероятнее всего вблизи боровского радиуса.
Для 2s-состояния будет наблюдаться 1 узел:

Рис. 7. «R(r) для 2s состояния (r измеряется в единицах a0)»
А для вероятности:

Рис. 8. «ρ(r) для 2s состояния (r измеряется в единицах a0)»
Сравним с вероятностью 2p-состояния:
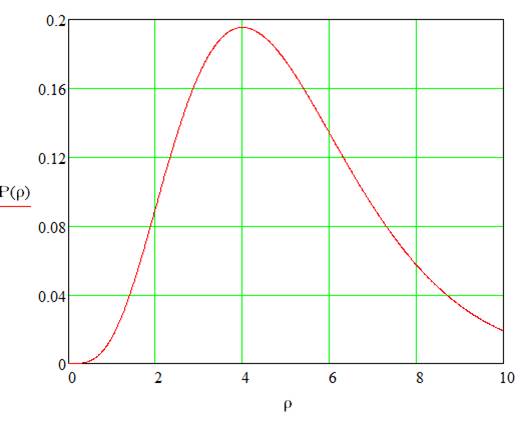
Рис. 9. «ρ(r) для 2p состояния (r измеряется в единицах a0)»
Мы получили интересную вещь. Главный максимум 2s-состояния находится ближе к ядру, чем максимум 2p-состояния, чего и следовало ожидать, но вот побочный максимум 2s-состояния (самый большой) находится дальше от ядра, чем 2p-состояния, то есть 2p-электроны просачиваются глубже, нежели 2s-электроны. Говорят, что ядро экранируется 2p-электронами. Аналогичное явление будет в сравнении 4s- и 3d-состояний. Такие нюансы распределения электронной плотности и эффекты экранировки ядра являются важными факторами при расчёте энергии связи в многоэлектронных системах.
Итоги.
Оказалось, электрон в поле кулоновского потенциала имеет дискретные энергетические уровни, вырожденные 2l+1 раз (без учёта спина). Энергия каждого уровня пропорциональна 1/n2, где n – главное квантовое число. На каждом уровне существуют подуровни, называемые орбиталями. Форма орбитали определяется числом l, которое называют орбитальным квантовым числом. Формы орбиталей при различных l приведены на рис. 4. Ориентация орбитали в пространстве определяется числом m, пробегающим значение от –l до l, и называемым магнитным квантовым числом. Были найдены волновые функции некоторых состояний электрона в атоме водорода, а также исследовано поведение радиальной волновой функции как в близи ядра, так и на произвольном расстоянии от него. Также было исследовано распределение электронной плотности ρ(r) для различных состояний. Оказалось, что некоторые состояния могут «просачиваться» сквозь другие ближе к ядру и экранировать его, что стоит учитывать при исследовании многоэлектронных систем.
Дата добавления: 2021-07-19; просмотров: 73; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
