IV . «СИСТЕМЫ ЛИНЕЙНЫХ НЕОДНОРОДНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ»

-
- система m линейных уравнений с n переменными, где произвольные числа 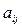
 - коэффициенты при переменных,
- коэффициенты при переменных, 
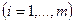 - свободные члены уравнений.
- свободные члены уравнений.
Решением такой системы называется совокупность значений переменных х1, …, х n , при подстановке которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы называются равносильными, если они имею одно и тоже множество решений.
Получают их с помощью элементарных преобразований:
1. изменение порядка уравнений в системе;
2. умножение или деление обеих частей любого уравнения системы на одно и то же неравное нулю число;
3. почленное сложение уравнений системы.
Рассматриваемую систему уравнений можно записать в матричной форме:
 , где
, где
А – матрица коэффициентов при переменных, или матрица системы;
Х – матрица–столбец переменных;
В – матрица–столбец свободных членов, т.е.
 ;
;  ;
;  .
.
Мы будем рассматривать системы, где m=n, т.е. количество уравнений в системе и количество входящих в них переменных равны. Тогда матрица А системы квадратная и имеет определитель 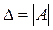 , который называют определителем системы.
, который называют определителем системы.
|
|
|
Такие системы можно решить одним из трех следующих методов:
1. метод Крамера;
2. матричный метод;
3. метод Гаусса.
V . «МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ НЕОДНОРОДНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ »
1. «Метод Крамера».
Теорема Крамера: Пусть определитель матрицы 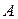 системы D, а
системы D, а 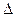 j – определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если
j – определители матриц, получаемых из данных заменой j-го столбца на столбец свободных членов. Тогда, если  , то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА:
, то система имеет единственное решение, которое вычисляется по формулам КРАМЕРА: 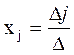 , где j=1; …;
, где j=1; …; 
| Алгоритм метода Крамера | Пример. Решить систему уравнений методом Крамера: 
| |
1. Записать матрицу  системы и найти ее определитель D, если D = 0 , то система решений не имеет. системы и найти ее определитель D, если D = 0 , то система решений не имеет.
| 1. | |
| 2. Если | 2. 

| |
| 3. По формулам Крамера находим х
|  Ответ: Ответ: 
| |
2. «Матричный метод».
Если определитель матрицы  системы
системы  , то матрица системы невырожденная, а значит, имеет обратную матрицу
, то матрица системы невырожденная, а значит, имеет обратную матрицу  . Умножим обе части матричного равенства
. Умножим обе части матричного равенства 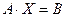 на обратную матрицу
на обратную матрицу  слева, получим равенство:
слева, получим равенство:  , или
, или  , откуда
, откуда  - равенство, выражающее суть матричного метода.
- равенство, выражающее суть матричного метода.
|
|
|
| Алгоритм матричного метода | Пример:
Решить систему матричным методом.
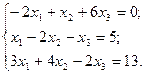
|
| 1. Записать матрицу системы и найти ее определитель. Если определитель равен нулю, то система не имеет решений. |  -система имеет решение, матрица системы имеет обратную. -система имеет решение, матрица системы имеет обратную.
|
2. Ищем матрицу  , обратную матрице , обратную матрице  системы по формуле системы по формуле 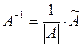 , где , где 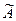 связана с связана с 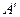 (нужно транспонировать матрицу (нужно транспонировать матрицу  ). ).
|  ; ;  Заменяем элементы транспонированной матрицы
Заменяем элементы транспонированной матрицы 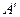 их алгебраическими дополнениями: их алгебраическими дополнениями:
 
 Теперь запишем
Теперь запишем 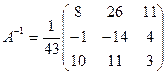 , и так и оставляем (для удобства последующих вычислений). , и так и оставляем (для удобства последующих вычислений).
|
3. Ищем матрицу – столбец  значений переменных системы по формуле значений переменных системы по формуле 
|  Ответ: Ответ:  . .
|
3. «Метод Гаусса».
Или метод последовательного исключения переменных - заключается в том, что с помощью элементарных преобразований данная система уравнений приводится к равносильной системе уравнений ступенчатого (треугольного) вида, из которой, последовательно, начиная с последней переменной, находятся все остальные переменные.
Системой треугольного (ступенчатого ) вида называется система вида
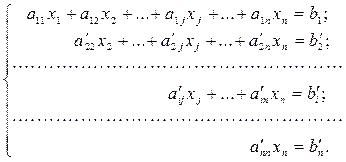
Получают такую систему с помощью следующих элементарных преобразований систем линейных неоднородных алгебраических уравнений:
|
|
|
1. изменение порядка уравнений системы,
2. умножение или деление обеих частей любого уравнения системы на одно и то же не равное нулю число,
3. почленное сложение уравнений системы.
Дата добавления: 2021-07-19; просмотров: 75; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

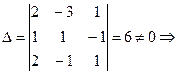 система имеет единственное решение.
система имеет единственное решение. :
: