Дробно-рациональные уравнения
Методика решения дробно - рациональных уравнений.
Подготовка учащихся к ОГЭ.
Кодификатор требований к уровню подготовки обучающихся для проведения основного государственного экзамена по математике является одним из документов, определяющих структуру и содержание КИМов. В нем сформулированы требования к уровню подготовки выпускников основной школы. В разделе III прописано требование «Уметь решать уравнения, неравенства и их системы»
| Код раздела | Код контролируемого умения | Уметь решать уравнения, неравенства и их системы |
| 3 | 3.1 | Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы |
| 3.2 | Решать линейные и квадратные неравенства с одной переменной и их системы | |
| 3.3 | Применять графические представления при решении уравнений, систем, неравенств | |
| 3.4 | Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений исходя из формулировки задачи |
С темой «Дробные рациональные уравнения » учащиеся впервые знакомятся на уроках алгебры в 8 классе. Вводится понятие дробно-рационального уравнения, указывается чёткий алгоритм его решения, разбираются базовые примеры. В 9 классе при изучении главы II «Уравнения и неравенства с одной переменной» расширяем знания учащихся по теме «Дробные рациональные уравнения», решаем более сложные задания. Результаты обучения в значительной степени зависят от конкретной методики обучения, которую применяет учитель на уроках. Учитель, при активном сотрудничестве с обучающимися, должен помочь им выделить систему общих указаний, которые будут служить ориентирами при решении уравнений.
|
|
|
Целесообразно четко сформулировать алгоритм решения дробно-рационального уравнения:
1) найти общий знаменатель дробей, входящих в уравнение;
2) умножить обе части уравнения на общий знаменатель;
3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
В ходе решения дробно-рациональных уравнений необходимо установить, являются ли найденные корни целого уравнения допустимыми значениями переменной. Учащиеся нередко ошибаются, пропуская этот момент, поэтому надо настойчиво добиваться, чтобы в каждом случае алгоритм был выполнен до конца.
Важно научить обучающихся пользоваться «методом пристального взгляда» чтобы они зрительно видели разложение знаменателей на простые множители и безошибочно находили наименьший общий знаменатель. Такая методика решения уравнений позволяет школьникам не допускать ошибок при решении дробных рациональных уравнений, успешно решать задачи с помощью дробных рациональных уравнений.
|
|
|
Следует также предварительно отработать умения и навыки учащихся при выполнении тождественных преобразований, решения квадратных и линейных уравнений, раскладывания квадратного трёхчлена на множители, нахождения ОДЗ, основного свойства пропорции, формул сокращённого умножения
Приемы решения дробных рациональных уравнений находят естественное и важное применение при решении текстовых задач. При решении текстовой задачи учащиеся выполняют три этапа, входящие в процесс решения:
- переводят задачу на язык алгебры (составляют математическую модель),
- решают полученное уравнение,
- выполняют содержательный анализ полученного ответа.
В практической деятельности при проведении уроков по этой теме я применяю организацию учебной деятельности следующим образом: обучающиеся работают по группам. Одна группа решает текстовые задачи – им требуется в процессе решения получить дробное рациональное уравнение. Другая группа работает над решением этих же уравнений. Последующая проверка у доски работы двух групп представляет полное решение текстовой задачи с обоснованной записью ответа. В зависимости от наполняемости класса можно организовать подобным образом работу четырех или шести групп. Такая организация урока позволяет активизировать мыслительную деятельность учащихся, развивает коммуникативные навыки, умение работать в сотрудничестве позволяет закрепить умение решать текстовые задачи и одновременно умение решать дробные рациональные уравнения.
|
|
|
Все выпускники 9 класса должны уметь решать дробные рациональные уравнения.
Чтобы достичь поставленной задачи учителю следует руководствоваться методическими требованиями к системе упражнений, направленной на организацию усвоения приемов решения дробных рациональных уравнений.
1. система упражнений должна обеспечивать возможность активного участия обучаемых в конструировании приема решения рассматриваемого класса задач (в нашем случае решения дробных рациональных уравнений)
2. система упражнений должна обеспечить усвоение и необходимое повторение каждого из приемов, входящих в качестве составной части в формируемый прием ( решения дробных рациональных уравнений)
|
|
|
3. система упражнений должна строиться по принципу систематичности, постепенного нарастания сложности, содержать задания комплексного характера, выполнение которых требует распознания типа уравнения и осознанного выбора способа его решения.
Дробно-рациональные уравнения
Стандартный вид дробно-рационального уравнения:

Где  – многочлены.
– многочлены.
Область допустимых значений (ОДЗ) данного уравнения:  Решение уравнений сводится к решению системы
Решение уравнений сводится к решению системы

Дробно-рациональные уравнения вида
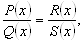
Где  – многочлены, можно решать, используя основное свойство пропорции:
– многочлены, можно решать, используя основное свойство пропорции:

Основные методы решения рациональных уравнений.
1. Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее.
Квадратные уравнения ax2 + bx + c = 0 решаются по формуле или используется теорема Виета: x1 + x2 = – b / a; x1x2 = c / a.
2.Способ группировки: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа — ноль. Затем приравниваем к нулю каждый из сомножителей.
3. Способ подстановки: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно какую следует сделать подстановку.
Например, уравнение
(x2 + x – 5) / x + 3x / (x2 + x – 5) + 4 = 0,
легко решается с помощью подстановки (x2 + x – 5) / x = t,
получаем t + (3 / t) + 4 = 0.
Или: 21 / (x2 – 4x + 10) – x2 + 4x = 6.
Здесь можно сделать подстановку x2 – 4 = t. Тогда 21 / (t + 10) - t = 6 и т.д.
В более сложных случаях подстановка видна лишь после нескольких преобразований. Например, дано уравнение
(x2 + 2x)2 – (x +1)2 = 55.
Переписав его иначе, а именно (x2 + 2x)2 – (x2 + 2x + 1) = 55, сразу увидим подстановку x2 + 2x=t.
Имеем t2 – t – 56 = 0, t1 = – 7, t2 = 8. Осталось решить x2 + 2x = – 7 и x2 + 2x = 8.
В ряде других случаев удобную подстановку желательно знать “заранее”. Например
Уравнение (x + a)4 + (x + b)4 = c сводится к биквадратному, если сделать подстановку
x = t – (a + b) / 2.
Симметрическое уравнение (возвратное) a0xn + a1xn – 1 + … + a1x + a0 = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1 / x = t, если n —чётное; если n — нечётное, то уравнение имеет корень x = – 1.
Уравнение вида (x + a)(x + b)(x + c)(x + d) = l сводится к квадратному, если
a + b = c + d и т.д.
К основному методу решения дробно-рациональных уравнений относится также метод замены переменной.
4. Подбор: при решении уравнений высших степеней рациональные корни уравнения anxn + an – 1xn – 1 + … + a1x + a0 = 0 ищем в виде p / q,
где p — делитель a0, q — делитель an, p и q взаимно просты, pÎ Z, qÎ N.
5. “Искусство”, т.е. решать пример нестандартно, придумать “свой метод”, догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.
|
Дата добавления: 2021-06-02; просмотров: 78; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 Решение. Сводим заданное уравнение к стандартному виду :
Решение. Сводим заданное уравнение к стандартному виду :
 т. е.
т. е. 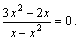 Его решением будет решение системы
Его решением будет решение системы
 т. е.
т. е. 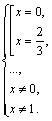 Значит, решением заданного уравнения является
Значит, решением заданного уравнения является 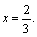 Ответ:
Ответ: 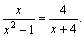 Решение. Применим основное свойство пропорции с учетом ОДЗ уравнения:
Решение. Применим основное свойство пропорции с учетом ОДЗ уравнения:
 Получаем:
Получаем:
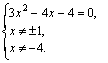 Откуда
Откуда
 Оба корня являются решениями, так как подходят по ОДЗ. В ответе имеем:
Оба корня являются решениями, так как подходят по ОДЗ. В ответе имеем:
 Ответ:
Ответ:  Решение. Группируем слагаемые
Решение. Группируем слагаемые
 Заменяем
Заменяем
 откуда
откуда
 т. е.
т. е.  и
и  Получаем уравнение
Получаем уравнение 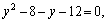 или, то же самое,
или, то же самое,  Полученное уравнение имеет корни:
Полученное уравнение имеет корни:  Возвращаемся к переменной Х:
Возвращаемся к переменной Х:
 В результате приходим к совокупности 2-х квадратных уравнений
В результате приходим к совокупности 2-х квадратных уравнений
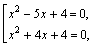 Которые решаем на ОДЗ:
Которые решаем на ОДЗ:  Приходим к ответу
Приходим к ответу
 Ответ:
Ответ: 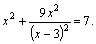 Решение. Выделим в левой части уравнения полный квадрат суммы:
Решение. Выделим в левой части уравнения полный квадрат суммы:
 Получаем уравнение, которое приобретает вид
Получаем уравнение, которое приобретает вид
 Заменяем
Заменяем 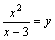 и приходим к уравнению
и приходим к уравнению
 Решая его, найдем корни:
Решая его, найдем корни:
 Возвращаемся к старой переменной:
Возвращаемся к старой переменной:
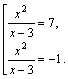 Решаем полученные уравнения по свойству пропорции (с учетом ОДЗ):
Решаем полученные уравнения по свойству пропорции (с учетом ОДЗ):
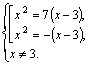 Ответ:
Ответ:  Пример 5. Решить уравнение
Пример 5. Решить уравнение  Решение. Введем замену:
Решение. Введем замену: 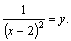 Тогда
Тогда 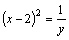 и получим уравнение
и получим уравнение  Решаем его:
Решаем его:
 т. е.
т. е.  Решая квадратное уравнение, находим корни:
Решая квадратное уравнение, находим корни:
 Вернемся к переменной Х:
Вернемся к переменной Х:
 Решаем первое уравнение:
Решаем первое уравнение:


 Второе уравнение не имеет решения, так как
Второе уравнение не имеет решения, так как  Ответ:
Ответ: