Дифференциальные уравнения с разделяющимися переменными

Тема 4.6. Дифференциальные уравнения

В приложениях математики к различным отраслям науки и техники дифференциальные уравнения занимают важное место. В отличие от алгебраических уравнений в дифференциальных уравнениях по некоторым заданным функциям требуется определить функцию, которая задается своими производными. Таким образом, дифференциальными уравнениями описываются более сложные процессы, происходящие в природе и технике.

Дифференциальным уравнением называется уравнение, содержащее независимую переменную х, искомую функцию у и ее производные у′, у′′,…

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.

Символически дифференциальное уравнение первого порядка записывается следующим образом:

F(x, y, y′) = 0 или у′ = f(x, y)

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Пример 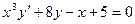- обыкновенное дифференциальное уравнение 1–го порядка.

- обыкновенное дифференциальное уравнение 2 – го порядка.

Решением дифференциального уравнения называется всякая функция у = φ(х), которая обращает данное уравнение в тождество.

Общим решением дифференциального уравнения называется функция у = φ(х,С), зависящая от постоянной С и удовлетворяющая данному уравнению при любом фиксированном значении этой постоянной.

Свойства общего решения

1) Т.к. постоянная С – произвольная величина, то, вообще говоря, дифференциальное уравнение имеет бесконечное множество решений.

2) При каких- либо начальных условиях х = х₀, у(х₀) = у₀ существует такое значение С = С₀, при котором решением дифференциального уравнения является функция у = j(х, С₀).

Частным решением дифференциального уравнения называется решение, полученное из общего решения при фиксированных значениях постоянной.

Задачей Коши называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

Теорема Коши(теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

Если функция f( x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную 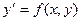, то какова бы не была точка (х₀, у₀) в области D, существует единственное решение уравнения 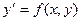, определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение j(х₀) = у₀, т.е. существует единственное решение дифференциального уравнения.

Пример. Найти общее решение дифференциального уравнения .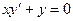

Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

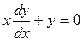
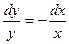
Теперь интегрируем: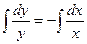

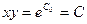
- общее решение исходного дифференциального уравнения.

Допустим, заданы некоторые начальные условия: x₀ = 1; y₀ = 2, тогда имеем

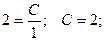
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение первого порядка у′ = f(x, y) называется уравнением с разделяющимися переменными, если его можно представить в виде:

у′ = f₁(x) ∙ f₂(y).

При решении дифференциальных уравнений с разделяющимися переменными полезно придерживаться следующей схемы:

- разделить переменные (т.е. в одной части уравнения должно быть выражение, содержащее только переменную х, в другой – переменную у);

- найти интегралы от обеих частей уравнения, найти частное решение уравнения;

- найти частное решение, удовлетворяющее начальным условиям (если они заданы).

Пример. Найти общее решение дифференциального уравнения: ydy + xdx = 0

Сначала разделим переменные, т.е. запишем уравнение в виде

ydy = - xdx,

затем найдем интегралы от обеих частей уравнения:

∫ ydy = -∫ xdx,

получим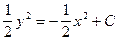

Пример. Найти общее решение дифференциального уравнения: 2уу′ = 1-3х².

Заменим у′ = и умножим обе части уравнения на dx.

Получим: 2у dy = (1-3х²)dx,

Затем найдем интегралы от обеих частей:

2∫ у dy = ∫(1-3х²)dx,

у² = х - х³+С.

Пример. Найти частное решение дифференциального уравнения (решить задачу Коши для заданных начальных условий): (1+x²)dy – 2x(y+3)dx = 0, если у = -1 при х = 0.

Сначала найдем общее решение. Разделим переменные (для этого выражение (– 2x(y+3)dx) перенесем в правую часть и разделим обе части уравнения на (1+x²)(y+3)).

Получим: ,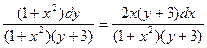

найдем интегралы от обеих частей:

Вычислим отдельно каждый интеграл.

1. 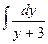. Введем новую переменную t = у+3, тогда dt = (у+3)′∙ d у = d у, т.е. dt = d у. Подставим новую переменную в интеграл:

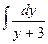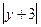= = ln + C = ln +C

2. 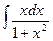. Введем новую переменную t = 1+x², тогда dt = (1+x²)′∙ dx = 2xdx, откуда dx = 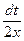. Подставим новую переменную в интеграл:

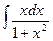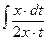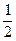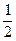= = = ln + C = ln

Найдем общее решение данного уравнения:

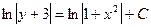
Для нахождения частного решения подставим в общее решение вместо х и у заданные начальные значения: ,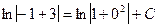

найдем С: С = ln 2,

подставим в общее решение получившееся значение C:

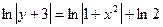
Пример. Найти общее решение дифференциального уравнения:

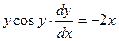
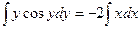
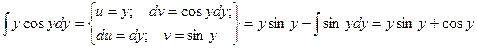
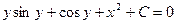это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.

Пример. Найти решение дифференциального уравнения при условии у(2)= 1.

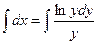
при у(2) = 1 получаем

или - частное решение;

Пример. Решить уравнение

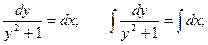
Пример. Решить уравнение при условии у(1) = 0.

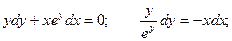
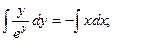
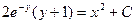
Если у(1) = 0, то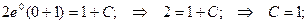

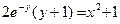Пример. Решить уравнение .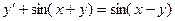

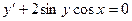
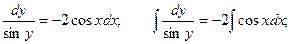
Пример. Решить уравнение

Преобразуем заданное уравнение:

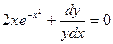
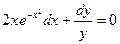
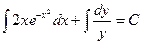
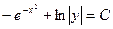
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.

Однородные уравнения

Функция f( x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Пример. Является ли однородной функция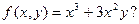

Таким образом, функция f(x, y) является однородной 3- го порядка.

Дифференциальное уравнение вида 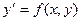называется однородным, если его правая часть f( x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида является однородным, если функции P( x, y) и Q( x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение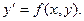

Т.к. функция f( x, y) – однородная нулевого измерения, то можно записать:

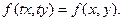
Т.к. параметр t вообще говоря произвольный, предположим, что 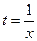. Получаем:

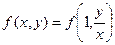
Правая часть полученного равенства зависит фактически только от одного аргумента , т.е.

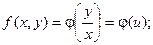
Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .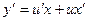

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

Далее, заменив вспомогательную функцию u на ее выражение через х и у и, найдя интегралы, получим общее решение однородного дифференциального уравнения.

Пример. Решить уравнение .

Введем вспомогательную функцию u.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

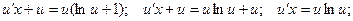
Разделяем переменные: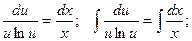

Интегрируя, получаем: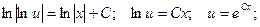

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

Дата добавления: 2021-06-02; просмотров: 56; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!