Число степеней свободы для общей суммы квадратов отклонений

Министерство Образования Российской Федерации

Тверской Государственный Технический Университет

Кафедра "Информационные системы"

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ЗАДАНИЯ

К КОНТРОЛЬНЫМ РАБОТАМ

по курсу

«ЭКОНОМЕТРИКА»

 

 

 

Тверь,2003

 

Предмет эконометрики и ее основные задачи

Эконометрика – раздел эконометрики, занимающейся разработкой и применением статистических методов для измерения взаимосвязей между эконометрическими переменными.

Эконометрика – единство трёх составляющих:

– статистики,

– экономической теории,

– математики.

Основные результаты экономической теории носят качественный характер, а эконометрика вносит в них эмпирическое (опытное) содержание.

Математика выражает математические законы в виде математических соотношений. Эконометрика осуществляет проверку этих законов.

Статистика дает информационное обеспечение исследуемого процесса в виде исходных статистических данных и показателей. Эконометрика проверяет количественные взаимосвязи между эмпирическими показателями.

Показатели разделяются на два вида:

– результирующие (зависимые),

– факторные (независимые, предикатные, объясняющие), то есть те, от которых зависят результирующие показатели.

Основная задача: получить (определить) ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных.

Наблюдаемое значение результирующей переменной зависит не только от факторных переменных, но и от случайных явлений, определяемых другими неучтенными факторами.

Общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части:

– объясняющую (детерминируемую)

– случайную.

Таким образом, основную задачу моделирования можно сформулировать следующим образом:

На основании эмпирических данных определить объясненную часть и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.

Линейный регрессионный анализ

 

В линейный регрессионный анализ входит широкий круг задач, свя­занных с построением (восстановлением) зависимостей между группами чи­словых переменных

Предполагается, что X - независимые переменные (факторы, объяс­няющие переменные) влияют на значения Y - зависимых переменных (результирующих, объясняемых переменных). По имеющимся эмпирическим данным (x_i, y_i), i = 1,...,n (n – число наблюдений) требуется построить функцию f(X), которая приближенно описывала бы изменение Y при изменении X:

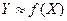
Предполагается, что множество допустимых функций, из которого подбирается f(X), является параметрическим:

f ( X ) = f ( X , Q ),

где Q - неизвестный параметр (вообще говоря, многомерный). При построении f(X) будем считать, что

Y = f ( X , Q )+e,                            (1)

 

где первое слагаемое - закономерное изменение Y от X, а второе - e - случай­ная составляющая с нулевым средним. f(X,Q ) является условным математическим ожиданием Y при условии известного X и называется рег­рессией Y no X .

Простая линейная регрессия

Пусть X и Y одномерные величины; обозначим их х и .у, а функция f ( x , Q) имеет вид f ( x , Q) = a+bx, где Q = ( a , b ). Относительно имеющихся наблюдений (x_i, y_i), i = 1,..., n, полагаем, что

y_i = a + bx_i + e _i                                   (2)

где e₁,…e_n- независимые одинаково распределенные случайные величины, определяющие действие различных неучтенных факторов на изменение результирующего показателя Y.

Уравнение (2) определяет простую (парную) линейную регрессию. Можно различными методами подбирать "лучшую" прямую линию, изменяя параметры a и b. На практике широко используется метод наименьших квадратов (МНК), суть которого заключается в следующем.

По­строим оценку параметра Q = ( a , b ) так, чтобы величины

e_i = y_i – f(x_i, Q ) = y_i – a - bx_i

называемые остатками, были как можно меньше, а именно, чтобы сумма их квадратов была минимальной:

                    (3)

Сумму минимимизируем по (а,b),приравнивая нулю производные по аи b.В результате получим систему уравнений линейных относительно aи b. Ее решение 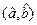 легко находится:

                 (4) и (5)

Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции r_yx. Для линейной регрессии (-1≤r_yx≤1)

 

       r_yx = bσ_x/σ_y

σ_{x =} , σ_{y =}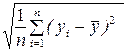          

и индекс корреляции ρ_yx – для нелинейной регрессии (0≤ρ_yx≤1)

 

ρ_yx = , ,

где  - дисперсия результирующего показателя y;  - дисперсия отклонений наблюдаемых значений результирующего показателя y_i от рассчитанных по уравнению регрессии .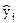

    Качество построенной модели можно оценить с помощью коэффициента (индекса) детерминации:

R² = = = 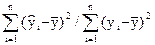ρ²_yx,

здесь - дисперсия, объясняемая регрессией. Чем больше значение этого показателя ( а оно изменяется от 0 до 1), тем лучше уравнение регрессии объясняет рассеяние наблюдаемых значений результирующего показателя y относительно средней величины, тем меньшее влияние на это рассеяние оказывают случайные факторы. Это видно из соотношения:

Задача дисперсионного анализа состоит в анализе дисперсии результирующего показателя.

Для получения несмещенной оценки дисперсии случайной величины сумму квадратов отклонений от среднего значения делят не на число наблюдений – n, а на число степеней свободы – df.

Число степеней свободы равно разности между числом неизвестных наблюдений случайной величины и числом связей, ограничивающих свободу их изменений, т. е. числом уравнений, связывающих эти наблюдений.

Число степеней свободы для общей суммы квадратов отклонений

df_общ = n-1.

Для суммы квадратов отклонения, объясненных регрессией df_рег = 1.

Для остаточной суммы квадратов отклонения df_ост = n-2.

n – число наблюдений.

Между степенями свободы определяются соответствия:

    df_общ = df_рег + df_ост

 Разделив каждую сумму квадратов отклонений на соответствующее число степеней свободы, получим величину – средний квадрат отклонения на одну степень свободы.

Эти величины используются для проверки уравнения регрессии. Проверяются гипотезы о существенности уравнения регрессии; о значимости коэффициентов уравнения регрессии; о значимости коэффициента корреляции.

Для проверки гипотезы о существенности уравнения регрессии используется F-критерий Фишера.

Способ 1.

Изначально принимается гипотеза Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого вычисляется

F-статистика:

.

Определяется табличное значение F_df1,df2,α при заданном уровне значимости α и степенях свободы df₁ = 1, df₂ = n-2.

Данное значение можно определить по таблице. Оно представляет собой процентную точку, которая определяется из уравнения:

         

α – уровень значимости, т.е. некоторая маленькая вероятность (например – 0,05), определяющая надежность полученных оценок.

Р(F) – плотность распределения вероятности Фишера со степенями свободы df₁, df₂.

Если F_pасч> F_df1,df2,α (рассчитанное значение больше, чем табличное)  точка попала в зону α – зону отклонения  гипотеза H₀ отклоняется и признается статистическая значимость и надежность уравнения регрессии и коэффициента детерминации.

Обычно 1-ый способ проверки значимости используется для ручных расчетов.

Способ 2.

В пакетах программ используется другой способ проверки – вычисляется P -уровень, т.е. значение вероятности, соответствующее расчетному значению F-критерия.

 

 

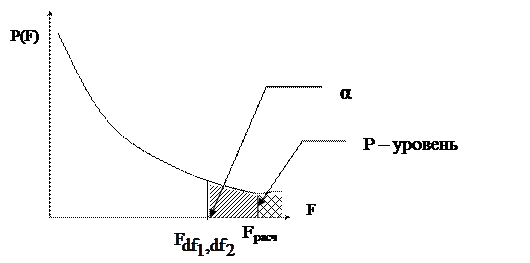
Если P<α, то гипотезу H₀ следует отвергнуть, т.е. признать статистическую значимость и надежность уравнения регрессии и коэффициента детерминации. Чем меньше значение P-уровня, тем надежнее полученные оценки.

Величина F-критерия связана с коэффициентом детерминации R²:

 .

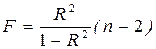Проверка существенности уравнения регрессии с помощью F-критерия проводится при условии нормальности распределения ошибки регрессии.

При таком же предположении можно проверить гипотезы относительно каждого коэффициента с использованием Т-статистики Стьюдента:

а, b – коэффициенты уравнения регрессии,

r – коэффициент корреляции.

t-статистика для коэффициента уравнения регрессии а – ;

t-статистика для коэффициента уравнения регрессии b – ;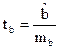

t-статистика для коэффициента корреляции r – .

m_a, m_b, m_r – стандартные ошибки.

; ; .

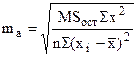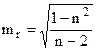Для проверки значимости этих коэффициентов необходимо сравнить полученные расчетные значения t_a, t_b, t_r с табличным значением распределения Стьюдента с df степенями свободы и уровнем значимости α, т.е. с t_df,α (df = n-2).

Если расчетное значение по абсолютной величине больше табличного, то нулевая гипотеза H₀

Н₀: а =0,

Н₀: b = 0,

Н₀: r = 0.

отвергается и значение соответствующего коэффициента считается значимым при данном уровне значимости α.

Связь между F-критерием Фишера и t – статистикой Стьюдента выражается равенством:

 = .

Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равна проверке гипотезы о существенности уравнения регрессии.

Качество уравнения регрессии можно также оценить с помощью средней ошибки аппроксимации

 

Множественная регрессия

 

Обобщением линейной регрессионной модели с двумя переменными является многомерная регрессионная модель (или модель множественной регрессии). Уравнение линейной регрессии . В экономике широко используется степенная функция вида: 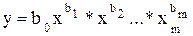. Эта функция используется для изучения спроса и потребления, для построения производственной функции, где y – выпуск, а x – факторы производства и др.

Коэффициенты линейной модели уравнения регрессии называются коэффициентами чистой регрессии. В случае полинома  коэффициенты характеризуют среднее изменение результата, при изменении соответствующего фактора на одну единицу и при неизменной величине остальных факторов.

В степенной функции коэффициенты чистой регрессии показывают, на сколько процентов изменится результат, при изменении соответствующего фактора на один процент и при фиксированном значении остальных факторов. Они играют роль коэффициентов эластичности.

Решение уравнения регрессии находится с помощью метода наименьших квадратов. Анализ полученного решения заключается в проверке полученного уравнения регрессии путем расчета коэффициента множественной детерминации:

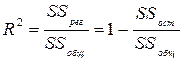
и F – статистики:

.

Если известен коэффициент детерминации R², то F – статистка может быть рассчитана следующим образом:

Рассчитанное значение сравнивается с табличным F_df1,df2,α ( ), где m – число независимых переменных, n – число наблюдений. Либо для расчетного значения F – статистики определяется P – уровень, который сравнивается с уровнем значимости α, так как это было описано в предыдущем разделе.

Недостатком коэффициента детерминации является то, что он увеличивается при добавлении новых переменных, хотя это и не обязательно означает улучшения качества регрессионной модели. Поэтому лучше пользоваться скорректированным коэффициентом детерминации, который определяется по формуле:

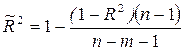
Уравнение регрессии может быть преобразовано к стандартизованному масштабу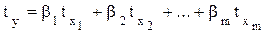

, где j – номер переменной.

Значения коэффициентов b_j можно определить из уравнения:

,

где  - коэффициенты взаимной корреляции между x_k  и x_j.

Основное достоинство стандартизованного уравнения регрессии в том, что стандартизованные коэффициенты b_j сравнимы между собой и позволяют ранжировать факторы по степени их воздействия на результат.

Коэффициенты чистой регрессии b_j связаны со стандартизованными коэффициентами b_j соотношением

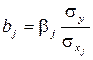
Проверка значимости коэффициентов регрессии аналогична проверке коэффициентов парной регрессии и сводится к вычислению значения

,

где - средняя квадратическая ошибка коэффициента регрессии b_j

КОНТРОЛЬНАЯ РАБОТА

Решение с помощью MS Exel

Для построения регрессии и ее анализа можно использовать встроенную статистическую функцию ЛИНЕЙН или инструмент анализа данных Регрессия.

1. ЛИНЕЙН

- введите исходные данные;

- выделите область пустых ячеек для вывода результатов;

- вызовите статистическую функцию ЛИНЕЙН;

- заполните аргументы функции, щелкните по кнопке OK;

- в левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу F2, а затем – на комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме.

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b - mb	Среднеквадратическое отклонение a - ma
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F - статистика	Число степеней свободы
SSрег	SSост

 

2.С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов, можно получить остатки и графики подбора линии регрессии, остатков и нормальной вероятности. Порядок действия следующий:

- в главном меню выберите Сервис/Анализ данных/Регрессия. Щелкните по кнопке OK;

- заполните диалоговое окно ввода данных и параметров вывода. Щелкните по кнопке OK;

Пример использования функции ЛИНЕЙН и инструмента анализа Регрессия приведен в файле Пример.xls.

 

Контрольное задание

Исследуется зависимость урожайности у зерновых культур ( ц/га ) от ряда факторов (переменных) сельскохозяйственного производства, а именно,

X1 - число тракторов на 100 га;

X2 - число зерноуборочных комбайнов на 100 га;

X3 - число орудий поверхностной обработки почвы на 100 га;

X4 - количество удобрений, расходуемых на гектар (т/га);

X5- количество химических средств защиты растений, расходуемых на гектар (ц/га).

Исходные данные для 20 районов области приведены в таблице.

 

	y	X1	X2	X3	X4	X5
1	9,7	1,59	,26	2,05	,32	,14
2	8,4	,34	,28	,46	,59	,66
3	9,0	2,53	,31	2,46	,30	,31
4	9,9	4,63	,40	6,44	,43	,59
5	9,6	2,16	,26	2,16	,39	,16
6	8,6	2,16	,30	2,69	,32	,17
7	12,5	,68	,29	,73	,42	,23
8	7,6	,35	,26	,42	,21	,08
9	6,9	,52	,24	,49	,20	,08
10	13,5	3,42	,31	3,02	1,37	,73
11	9,7	1,78	,30	3,19	,73	,17
12	10,7	2,40	,32	3,30	,25	,14
13	12,1	9,36	,40	11,51	,39	,38
14	9,7	1,72	,28	2,26	,82	,17
15	7,0	,59	,29	,60	,13	,35
16	7,2	,28	,26	,30	,09	,15
17	8,2	1,64	,29	1,44	,20	,08
18	8,4	,09	,22	,05	,43	,20
19	13,1	,08	,25	,03	,73	,20
20	8,7	1,36	,26	,17	,99	,42

 

Здесь мы располагаем выборкой объема п = 20; число независимых переменных (факторов) m = 5.

Необходимо:

- построить уравнения линейной регрессии, последовательно увеличивая число факторных переменных от одной до пяти;

- определить качество полученных уравнений регрессии и их статистическую значимость;

- оценить статистическую значимость параметров регрессии;

- построить графики остатков для полученных регрессий;

- рассчитать нормированные коэффициенты b _j

Варианты задания определяются следующим образом.

 

В исходной таблице величина результирующего показателя y изменяется в зависимости от Вашего номера в списке группы. Для этого к значению текущего наблюдения y_i прибавляется значение Вашего номера умноженное на 0,05. Например, если Ваш номер в группе 10, то значения во второй колонке таблицы будут:

y₁ = 9,7 +10*0,05 = 10,2

y₂ = 8,4 +10*0,05 = 8,9

y₃ = 9,0 +10*0,05 = 9,5 и так далее….

Остальные колонки остаются без изменения.

 

Литература

1. Эконометрика. /ред. Елисеева И.И. - М.: Финансы и статистика. 2002. – 344с.

2. Эконометрика / ред. Кремер Н.Ш. – М.: ЮНИТИ – ДАНА, 2002. – 311с.

3. Практикум по эконометрике / ред. Елисеева И.И. - М.: Финансы и статистика. 2001. – 192с.

---

Дата добавления: 2021-03-18; просмотров: 113; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!