Координаты правильной треугольной призмы
Решение заданий №14 ЕГЭ по математике координатно-векторным методом
Методические рекомендации.
С помощью данных методических рекомендаций можно научиться решать задачи на вычисление углов и расстояний в стереометрии с помощью координатно-векторного метода. Для учеников 10-11 классов самой главной проблемой является подготовка к ЕГЭ. Причем не все ученики уверенно решают задания II части , а некоторые и не берутся за их решение.
Координатно-векторный метод основан на введении прямоугольной системы координат и создании геометрически-алгебраической модели решения задач, тем самым упрощая громоздкие и достаточно сложные преобразования и выкладки.
Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций.
Выражаю огромную благодарность своим ученикам 11 класса 2016 – 2017 учебного года: Комаровой Ангелине, Тарбаеву Наилю, Бекмурзаеву Тимуру, Утегеновой Аимгуль, Абылхатаевой Карине, Кункашевой Арине, Юсуповой Аделине, Успанову Гелиму, которые сыграли большую роль в создании данного методического сборника
Уважаемые ребята!
Если у вас имеются серьезные проблемы с пониманием определений, с чтением или построением сложного стереометрического рисунка, если вам никак не удается подобрать необходимые дополнительные построения, мне кажется, что стоит заняться изучением координатно-векторного метода. Особенно это актуально в условиях экстренной помощи, когда до ЕГЭ остается всего лишь 2-3 месяца.
|
|
|
Данный курс не претендует на научность, а является небольшим методическим пособием при подготовке к ЕГЭ для выпускника, нацеленного на высокий балл при сдаче экзамена. Курс является кратким, в нем рассмотрены лишь наиболее часто встречающиеся типы заданий, как в сборниках, так и в контрольно-измерительных материалах.
Метод координат — это довольно несложный способ, но в настоящих задачах №14 никаких координат и векторов нет. Поэтому их придется вводить: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Успехов!
Основные понятия.
Метод координат —эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Данный метод заключается во введении декартовой системы координат, а затем – нахождение образующихся векторов (их длин и углов между ними). Достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных конфигураций. Алгоритм применения метода координат к решению геометрических задач сводится к следующему:
|
|
|
- Выбираем в пространстве систему координат
- Находим координаты необходимых, по условию задачи, точек.
- Решаем задачу, используя основные задачи метода координат.
- Переходим от аналитических соотношений к геометрическим.
Для начала разбора метода координат для стереометрических задач рассмотрим, что же представляет собой прямоугольная (декартова) система координат в пространстве. Прямоугольная (декартова) система координат в пространстве – совокупность точки О (называемой началом координат), единицы измерения и трёх попарно перпендикулярных прямых Ox, Oy иOz (называемых осями координат: Ox – ось абсцисс, Oy – ось ординат, Oz – ось аппликат), на каждой из которых указано направление положительного отсчёта. Плоскости хОу, уОz и zOx называют координатными плоскостями. Каждой точке пространства ставится в соответствие тройка чисел, называемых её координатами.
|
|
|
 z
z
 |
 0 у
0 у
х
Для того чтобы использовать метод координат, надо хорошо знать формулы:
1. Нахождение расстояния между двумя точками, заданными своими координатами.
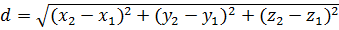 , где
, где
D=AB, A(x1;y1;z1), B(x2;y2;z2)
2. Нахождение координат середины отрезка
A(x 1 ; y 1 ; z 1), B(x 2 ; y 2 ; z 2) 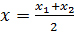
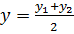
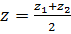
3. Нахождение косинуса угла между векторами
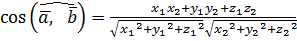 , где
, где 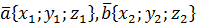
4. Координаты x, y, z точки М, которая делит отрезок , ограниченный точками А(х1, у1,z1 ) и B(x2,y2,z2 ), в отношении , определяется по формулам 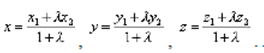
5. Расстояние от точки до плоскости
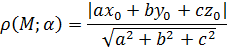
Для решения задач необходимо научиться находить координаты вершин основных многогранников при помещении их в прямоугольную систему координат.
Ниже представлены координаты вершин некоторых многогранников, помещенных в систему координат.
Координаты куба
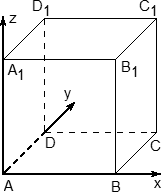
Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
1. Начало координат — в точке A;
2. Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
3. Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
|
|
|
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень удобно и логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются от соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1).
Координаты правильной треугольной призмы
При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах №14 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба.
Вводим систему координат:
1. Начало координат — в точке A;
2. Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
3. Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.

Получаем следующие координаты точек:
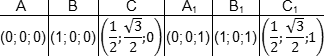
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, и для того чтобы довольно просто решить задание №14 эти иррациональные координаты надо просто запомнить. Или можно вывести.
Дата добавления: 2021-03-18; просмотров: 1261; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
