Возведение комплексного числа в натуральную степень
Возведение в натуральную степень удобнее выполнять в тригонометрической форме:
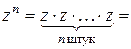
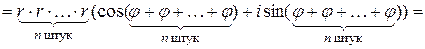

В результате получается формула Муавра:
 Формула Муавра,(9)
Формула Муавра,(9)
то есть при возведении комплексного числа в натуральную степень его модуль возводится в эту степень, а аргумент умножается на показатель степени.
Пример
Вычислить (1 + i)10.
Решение:
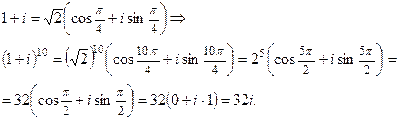
Замечания
1. При выполнении операций умножения и возведения в натуральную степень в тригонометрической форме могут получаться значения углов  за пределами одного полного оборота. Но их всегда можно свести к углам
за пределами одного полного оборота. Но их всегда можно свести к углам  или
или  сбрасыванием целого числа полных оборотов по свойствам периодичности функций
сбрасыванием целого числа полных оборотов по свойствам периодичности функций  и
и 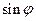 .
.
2. Значение 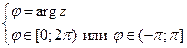 называют главным значением аргумента комплексного числа
называют главным значением аргумента комплексного числа  ;
;
при этом значения всех возможных углов  обозначают
обозначают  ;
;
очевидно, что  ,
, 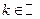 .
.
Извлечение корня натуральной степени из комплексного числа
Корнем степени n из комплексного числа z, где  N, называется комплексное число w, такое что w n = z
N, называется комплексное число w, такое что w n = z 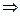
 .
.
Примеры
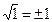 , так как
, так как  ;
;
 , так как
, так как  ;
;
 или
или  , так как
, так как  и
и  .
.
Из определения очевидно следует, что операция извлечения корня из комплексного числа является многозначной.
Если использовать формулу Муавра, то нетрудно доказать следующее утверждение:
 существует при "z и если z ¹ 0, то
существует при "z и если z ¹ 0, то  имеет n различных значений, вычисляемых по формуле
имеет n различных значений, вычисляемых по формуле
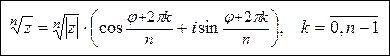 Извлечение корня натуральной степени из комплексного числа ,(10)
Извлечение корня натуральной степени из комплексного числа ,(10)
|
|
|
где 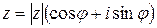 ,
,
 — арифметический корень на
— арифметический корень на  .
.
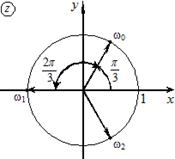
Все значения  расположены регулярным образом на окружности радиусом
расположены регулярным образом на окружности радиусом  с начальным углом
с начальным углом  и углом регулярности
и углом регулярности  .
.
Примеры
1) 
 , k = 0, 1, 2 Þ
, k = 0, 1, 2 Þ
Þ 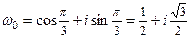 ,
,
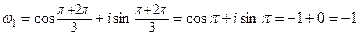 ,
,
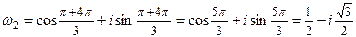 .
.
Ответ: 
2)  ,
, 

 .
.
4) Формулы Эйлера . Формула Муавра
Используем определение  Þ
Þ  ,
,
так как  ,
,  .
.
Из этих равенств следуют формулы Эйлера
 Формулы Эйлера(11)
Формулы Эйлера(11)
по которым тригонометрические функции  и
и  действительной переменной
действительной переменной  выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.
выражаются через показательную функцию (экспоненту) с чисто мнимым показателем.
 Формула Муавра,(12)
Формула Муавра,(12)
Рациональные функции
1.Рациональные дроби. Теорема Безу
Определение. Функция вида f ( x )  называется целой рациональной функцией от х.
называется целой рациональной функцией от х.
Теорема Безу. (Этьенн Безу (1730 – 1783) – французский математик)
При делении многочлена f ( x ) на разность x – a получается остаток, равный f ( a ).
Доказательство. При делении многочлена f ( x ) на разность x – a частным будет многочлен f 1 ( x ) степенина единицу меньшей, чем f ( x ), а остатком – постоянное число R.

Переходя к пределу при х ® a , получаем f ( a ) = R .
Следствие. Если, а – корень многочлена, т.е. f ( a ) = 0, то многочлен f ( x ) делится на (х – а) без остатка.
|
|
|
Определение. Если уравнение имеет вид Р(х) = 0, где Р(х) – многочлен степени n, то это уравнение называется алгебраическим уравнением степени n.
Теорема. (Основная теорема алгебры) Всякая целая рациональная функция f ( x ) имеет, по крайней мере, один корень, действительный или комплексный.
Теорема. Всякий многочлен n – ой степени разлагается на n линейных множителей вида ( x – a ) и множитель, равный коэффициенту при xn .
Теорема. Если два многочлена тождественно равны друг другу, то коэффициенты одного многочлена равны соответствующим коэффициентам другого.
Если среди корней многочлена встречаются кратные корни, то разложение на множители имеет вид:

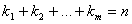
ki - кратность соответствующего корня.
Отсюда следует, что любой многочлен n – ой степени имеет ровно n корней (действительных или комплексных).
Это свойство имеет большое значение для решения алгебраических уравнений, дифференциальных уравнений и играет важную роль в анализе функций.
| 2. О кратных и комплексных корнях многочлена | ||||||
Если в разложении многочлена  на множители (4) некоторые линейные множители окажутся одинаковыми, то их можно объединить, и тогда разложение многочлена на множители будет иметь вид: на множители (4) некоторые линейные множители окажутся одинаковыми, то их можно объединить, и тогда разложение многочлена на множители будет иметь вид:
При этом
Например, многочлен Имеет место теорема: всякий многочлен n–ой степени имеет ровно n корней (действительных или комплексных). Теорема (без доказательства). Если многочлен с действительными коэффициентами имеет комплексный корень Итак, в разложении (4) многочлена на множители комплексные корни входят попарно сопряженными. Перемножив линейные множители где Если корень Таким образом, многочлен с действительными коэффициентами разлагается на множители согласно формуле где
| ||||||
| 3. Разложение правильных рациональных дробей на простейшие | ||||||
Рассмотрим рациональную дробь 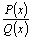 , где , где  и и  –многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена –многочлены с действительными коэффициентами. Рациональная дробь называется правильной, если степень многочлена  меньше степени многочлена меньше степени многочлена  .
Если рациональная дробь является неправильной, то произведя деление .
Если рациональная дробь является неправильной, то произведя деление  на на  по правилу деления многочленов, ее можно представить в виде по правилу деления многочленов, ее можно представить в виде 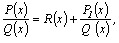 где где  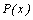 –некоторые многочлены, а –некоторые многочлены, а  –правильная рациональная дробь.
Правильные рациональные дроби вида –правильная рациональная дробь.
Правильные рациональные дроби вида
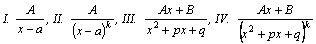 , где k–целое положительное число ≥2, дискриминант квадратного трехчлена , где k–целое положительное число ≥2, дискриминант квадратного трехчлена  отрицателен, называются простейшими дробями I, II, III и IV типов.
Правильную рациональную дробь, числитель и знаменатель которой не имеют общих корней, то есть дробь несократимую можно разложить на сумму простейших дробей.
Здесь имеют место три случая.
1.Все корни многочлена отрицателен, называются простейшими дробями I, II, III и IV типов.
Правильную рациональную дробь, числитель и знаменатель которой не имеют общих корней, то есть дробь несократимую можно разложить на сумму простейших дробей.
Здесь имеют место три случая.
1.Все корни многочлена  , стоящего в знаменателе, действительны и различны, то есть , стоящего в знаменателе, действительны и различны, то есть 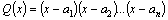 . Тогда . Тогда 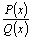 можно разложить на n простейших дробей I типа: можно разложить на n простейших дробей I типа:
2.Все корни многочлена
3.Среди корней знаменателя правильной рациональной дроби имеются комплексно сопряженные не повторяющиеся, то есть Тогда дробь
|
2.Простейшие дроби
Правильная рациональная алгебраическая дробь Q(x)P(x) называется простейшей, если ее знаменатель Q(x) является натуральной степенью некоторого неприводимого многочлена q(x):
Q(x)=q k(x),(k≥1),
а степень числителя P(x) меньше степени многочлена q(x). Напомним, что среди многочленов с действительными коэффициентами и со старшим коэффициентом, равным единице, неприводимыми являются лишь линейные многочлены x−c и квадратные многочлены x2+px+q при условии, что коэффициенты квадратного трехчлена удовлетворяют неравенству p2−4q<0 .
Вследствие этого рациональная алгебраическая дробь может быть простейшей лишь в случаях, когда ее числитель P(x) - либо многочлен первой степени, либо многочлен нулевой степени (т.е. число не равное нулю).
Пример. Дробь x−1(x2+1)k (k - натуральное) будет простейшей рациональной алгебраической дробью, так как ее знаменатель является степенью неприводимого многочлена , а степень неприводимого многочлена больше степени числителя.
В теории рациональных алгебраических дробей центральное место занимает следующая теорема:
Всякая правильная рациональная дробь разлагается в сумму простейших дробей, и это разложение единственно.
Точнее, если дана правильная дробь Q(x)P(x), знаменатель которой имеет разложение на неприводимые множители:
Q(x)=q1k1(x)q2k2(x)...q lk l(x), причем q i(x)/=q j(x) при i/=j и k1,k2,...,k l - натуральные числа, то
Q(x)P(x)=p1(x)q1k1(x)+p2(x)q2k2(x)+...+p l(x)q lk l(x),
где все слагаемые в правой части - правильные дроби, каждая из которых может быть представлена в виде суммы простейших дробей:
p(x)q k(x)=q k(x)S k(x)+q k−1(x)S k−1(x)+...+q2(x)S2(x)+q(x)S1(x).
Степени всех числителей, стоящих в правой части этого разложения, меньше степени многочлена q(x).
Дата добавления: 2021-03-18; просмотров: 88; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

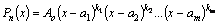
 . В этом случае корни
. В этом случае корни  называются корнями кратности
называются корнями кратности 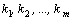 соответственно.
соответственно.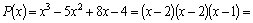
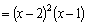 . Корень
. Корень  –двукратный корень этого многочлена,
–двукратный корень этого многочлена,  –простой корень.
–простой корень. , то он имеет и сопряженный корень
, то он имеет и сопряженный корень  .
. и
и 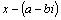 , соответствующие паре комплексно сопряженных корней, получим квадратный трехчлен с действительными коэффициентами:
, соответствующие паре комплексно сопряженных корней, получим квадратный трехчлен с действительными коэффициентами: 
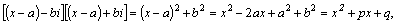
 –действительные числа.
–действительные числа. входят множители
входят множители  , то есть множители
, то есть множители 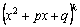 .
. ,
,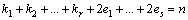

 . Тогда рациональную дробь можно разложить на сумму простейших дробей I и II типов:
. Тогда рациональную дробь можно разложить на сумму простейших дробей I и II типов: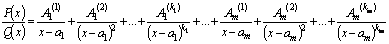 (8)
(8)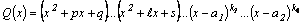 .
. знаменателя:
знаменателя: