Определение кривизны графика в точке и её вычисление.
Глава 5.
Тема2.
Исследование функции и построение эскиза её графика. Кривизна графика в точке.
Для наглядного описания функции часто используют её графическое представление. Как правило, такое представление бывает полезно для обсуждения качественных вопросов поведения исследуемой функции. Например: где функция пересекает ось ОХ, ось ОУ; на каких интервалах она возрастает и на каких убывает; есть ли у неё локальные экстремумы; каково направление выпуклости графика; имеются ли разрывы графика; какова асимптотика и так далее. Для точных расчетов графики функций используются редко. Однако бывает очень полезно изучить график перед проведением точных расчётов, так как из графического поведения функции видно какие алгоритмы и вблизи каких точек графика применять наиболее целесообразно. Для построения графика дифференцируемой функции 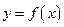 используют алгоритмы дифференциального исчисления. Рекомендуемый порядок исследования функции и построения её графика приведён ниже.
используют алгоритмы дифференциального исчисления. Рекомендуемый порядок исследования функции и построения её графика приведён ниже.
1)Указать область определения функции 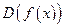 .
.
2) Указать нули функции, если это возможно.
3)Отметить конкретные особенности: чётность, периодичность.
5)Найти промежутки монотонности функции и указать её локальные экстремумы.
6)Уточнить характер выпуклости графика и указать точки перегиба графика.
7)Выяснить асимптотическое поведение функции: с указанием уравнений
|
|
|
вертикальных и наклонных асимптот.
8) Отметить характерные точки графика, например, точки пересечения графика функции с осью ОУ, если они есть и их возможно вычислить. Очень полезно вычислить две, три конкретные точки графика функции.
Далее рассмотрим примеры.
Пример 2.1. Исследовать функцию  и построить её график
и построить её график
1. Данная функция есть многочлен пятой степени. Область определения D многочлена интервал 
2. Определим нули функции. В данном случае это возможно

3. Функция нечётная, так как 
4. Определим участки монотонности и локальные экстремумы. Вычислим критические точки функции. У многочлена у всех критических точек 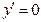 . Отсюда
. Отсюда 
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
Производная  положительна
положительна
на интервалах  . Производная отрицательна на интервалах
. Производная отрицательна на интервалах
 . Вычисляем значения функции в критических точках
. Вычисляем значения функции в критических точках
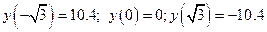 и заполняем таблицу.
и заполняем таблицу.
| x | - 
| 0 | 
| ||||
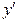
| + | 0 | - | 0 | - | + | |
| y | 
| 10.4 | 
| 0 | 
| -10.4 | 
|
Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной
|
|
|
получаем. При х =-  локальный максимум, при х=0 экстремума нет, при х=
локальный максимум, при х=0 экстремума нет, при х=  локальный минимум.
локальный минимум.
5. Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб».

Вторая производная 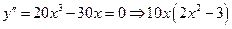 положительна
положительна
на интервалах  Производная отрицательна на интервалах
Производная отрицательна на интервалах
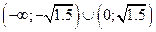 .Определяем точки подозрительные на перегиб.
.Определяем точки подозрительные на перегиб.
Вычисляем значения функции в точках подозрительных на перегиб
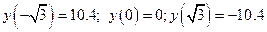 и заполняем таблицу.
и заполняем таблицу.
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | - 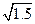
| 0 | 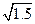
| ||||

| - | 0 | + | 0 | - | 0 | + |
| y | 
| -6.4 | 
| 0 | 
| 6.4 | 
|
Используя правило 1.2 нахождения точек перегиба с помощью второй производной, получаем, что точки 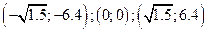 являются точками перегиба графика функции.
являются точками перегиба графика функции.
6. Исследуем функцию на асимптотическое поведение. Многочлен не имеет асимптот.
7. График пересекает ось ОУ в точке (0,0).
8. Используя таблицы, строим график функции
|
|
|

Пример 1.2. Исследовать функцию 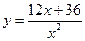 и построить её график
и построить её график
1. Данная функция это дробно- рациональная функция. Область определения D есть множество 
2. Определим нули функции. В данном случае это возможно
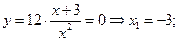
3.Функция общего вида
4. Определим участки монотонности и локальные экстремумы. Вычислим критические точки функции. В этих точках либо 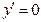 , либо
, либо  не существует.
не существует.
Вычисляем производную функции 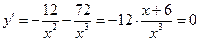 .
.
В точке 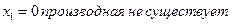 . В точке
. В точке 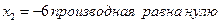 .
.
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
Производная  положительна
положительна
на интервале 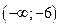 . Производная отрицательна на интервалах
. Производная отрицательна на интервалах
 . Вычисляем значения функции в критических точках.
. Вычисляем значения функции в критических точках.
В точке  ,
,  , в точке
, в точке  значения функции не существует.
значения функции не существует.
Заполняем таблицу.
| x | -6 | 0 | |||
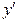
| + | 0 | - | 0 | - |
| y | 
| -1 | 
| 0 | 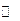 
|
Используя правило 1.1 ( нахождения локальных экстремумов с помощью первой производной)
получаем. При  локальный минимум, при х=0 экстремума нет.
локальный минимум, при х=0 экстремума нет.
5. Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб». Вторая производная равна  . В точке
. В точке  . Точка подозрительная
. Точка подозрительная
|
|
|
на перегиб имеет координаты  . Определяем знаки
. Определяем знаки 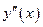 на интервалах.
на интервалах.
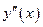 положительна на интервалах
положительна на интервалах  .
. 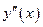 отрицательна на интервале
отрицательна на интервале  . Согласно правилу 1.2 точка
. Согласно правилу 1.2 точка  является точкой перегиба графика.
является точкой перегиба графика.
Для определения знаков второй производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -9 | 0 | |||

| - | 0 | + | нет | + |
| y | 
| -0,9 | 
| нет | 
|
6. Находим асимптоты графика функции. Асимптота это прямая, к которой неограниченно приближается график функции при  . Наклонная асимптота имеет уравнение
. Наклонная асимптота имеет уравнение 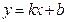 . Алгоритм нахождения параметров
. Алгоритм нахождения параметров  известен.
известен.
Сначала определяем  .
.
Затем определяем
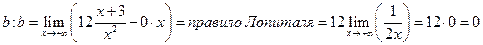
Уравнение наклонной асимптоты найдено  .
.
При  график также имеет асимптоту
график также имеет асимптоту  .
.
Легко находим, что  есть уравнение вертикальной асимптоты
есть уравнение вертикальной асимптоты

7. График не пересекает ось ОУ.
8. Используя таблицы, строим график функции

Пример 1.3. Исследовать функцию 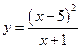 и построить её график
и построить её график
1. Данная функция это дробно- рациональная функция. Область определения D есть множество 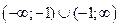
2. Определим нули функции. В данном случае это возможно
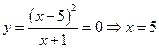
3.Функция общего вида .
4.с помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Стационарными точками являются точки, в которых  :
: 
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -7 | 5 | |||
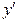
| + | 0 | - | 0 | + |
| y | 
| -24 | 
| 0 | 
|
Используя правило 1.1 нахождения локальных экстремумов получаем. При х=-7 локальный максимум, при х=5 локальный минимум.
5. С помощью второй производной  исследуем функцию на выпуклость. Находим точки «подозрительные на перегиб»
исследуем функцию на выпуклость. Находим точки «подозрительные на перегиб»
Точки, в которых производная равна нулю отсутствуют 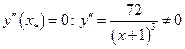 . Точка, в которых вторая производная не существует
. Точка, в которых вторая производная не существует  .
.
Для определения знаков второй производной слева и справа от точки  применяем метод интервалов и заполняем соответствующую таблицу
применяем метод интервалов и заполняем соответствующую таблицу
| x | -1 | ||

|

| нет | + |
| y | 
| нет | 
|
Точек перегиба графика нет.
6. Исследуем поведение функции на бесконечности.
Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно приближается график функции при  . Наклонная асимптота имеет уравнение
. Наклонная асимптота имеет уравнение 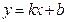 . Алгоритм нахождения параметров
. Алгоритм нахождения параметров  известен. Сначала определяем
известен. Сначала определяем  .
.
Затем

Уравнение наклонной асимптоты найдено 
Проверим , имеет ли данная функция вертикальную асимптоту.
Прямая, имеющая уравнение  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 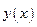 если
если 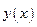 бесконечно большая при
бесконечно большая при  .
.
Так как  , то
, то
прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
7.График пересекает ось ОУ в точке (5,0).
8. Строим график функции.

Пример 1.4. Исследовать функцию  и построить её график
и построить её график
1. Область определения D функции интервал 
2.Определим нули функции. В данном случае это возможно

3.Так как  , то
, то 
функция нечётная.
4.С помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Такими точками являются точки в которых  :
:

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу
| x | -1 | 1 | |||
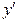
|

| 0 | + | 0 | 
|
| y | 
| -0,6 | 
| 0,6 | 
|
Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной
получаем. При х=-1 локальный минимум, при х=1 локальный максимум.
5.С помощью второй производной исследуем функцию на выпуклость. Находим точки «подозрительные на перегиб».В этих точках  или не существует
или не существует

Для определения знаков второй производной слева и справа от этих точек применяем метод интервалов и заполняем соответствующую таблицу
| x | - 
| 0 | 
| ||||

|

| 0 | + | 0 | 
| 0 | + |
| y |
| нет |

|

|

|
4. Исследуем функцию на асимптотическое поведение.
Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно приближается график функции при  . Наклонная асимптота имеет уравнение
. Наклонная асимптота имеет уравнение 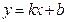 . Алгоритм нахождения параметров
. Алгоритм нахождения параметров  известен
известен
Сначала всегда определяем 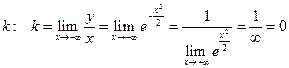 .
.
Затем 

П. Уравнение наклонной асимптоты найдено 
Так как функция  непрерывна, то вертикальных асимптот нет.
непрерывна, то вертикальных асимптот нет.
7. График пересекает ось ОУ в точке (0,0).
8. Строим график функции.

Определение кривизны графика в точке и её вычисление.
Рассмотрим дугу графика функции между точками 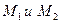 . Пусть в этих точках проведены касательные (рис. )
. Пусть в этих точках проведены касательные (рис. )
|


|


|


|

|

|


Рис.1
Соответствующие углы между касательными и осью  обозначим
обозначим 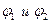 . При перемещении точки касания вдоль кривой от
. При перемещении точки касания вдоль кривой от 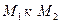 касательная прямая повернулась на угол
касательная прямая повернулась на угол  . Обозначим длину дуги
. Обозначим длину дуги 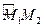 через
через  .
.
Дата добавления: 2021-03-18; просмотров: 100; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!