Область определения функции, в которой есть дробь
Преобразование графиков, симметрия относительно прямой, растяжение и сжатие.
Пусть задан график функции y = f(x). Чтобы построить график функции
- y = mf(x), где m > 0 и m ≠ 1, нужно ординаты точек заданного графика умножить на m. Такое преобразование называется растяжением от оси x c коэффициентом m, если m > 1, и сжатием к оси x, если 0 < m < 1.
- y = −f(x) получается из графика функции f(x) преобразованием симметрии относительно оси x. (Преобразование симметрии - зеркальное отражение относительно прямой.)
- y = f(x) + n, получается из графика функции f(x) параллельным переносом последнего вдоль оси ординат на n единиц вверх, если n > 0 и, соответственно на |n| единиц вниз, если n < 0.
- y = f(kx), где k > 0 и k ≠ 1. Искомый график функции получается из заданного сжатием с коэффициентомk к оси y (если 0 < k < 1 указанное "сжатие" фактически является растяжением с коэффициентом 1/k)
- y = f(−x) получается из графика функции f(x) преобразованием симметрии относительно оси y
- y = f(x + l) получается из графика функции f(x) параллельным переносом последнего на l единиц влево, если l > 0 и, соответственно на |l| единиц вправо, если m < 0.
Функции одной переменной  . Актуализирую два особо нужных сейчас термина: «икс» – независимая переменная или АРГУМЕНТ, «игрек» – зависимая переменная или ФУНКЦИЯ. При этом функцию можно обозначать как через «игрек», так равноценно и через «эф от икс», например:
. Актуализирую два особо нужных сейчас термина: «икс» – независимая переменная или АРГУМЕНТ, «игрек» – зависимая переменная или ФУНКЦИЯ. При этом функцию можно обозначать как через «игрек», так равноценно и через «эф от икс», например:

|
|
|
Сжатие (растяжение) графика к (от) оси ординат.
Симметричное отображение графика относительно оси 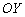
Первая группа действий связана с умножением АРГУМЕНТА функции на число. Для удобства я разобью правило на несколько пунктов:
Сжатие графика функции к оси ординат
Это случай когда АРГУМЕНТ функции умножен на число, бОльшее единицы.
Правило: чтобы построить график функции 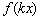 , где
, где 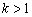 , нужно график функции
, нужно график функции 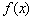 сжать к оси
сжать к оси 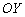 в
в 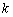 раз.
раз.
Пример 1
Построить график функции  .
.
Сначала изобразим график синуса, его период равен  :
:
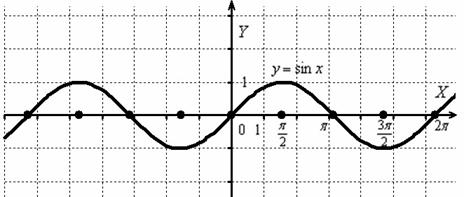
К слову, чертить графики тригонометрических функций вручную – занятие кропотливое, поскольку 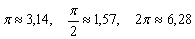
Теперь поиграем на бесконечно длинном баяне. Мысленно возьмём синусоиду в руки и сожмём её к оси  в 2 раза:
в 2 раза:
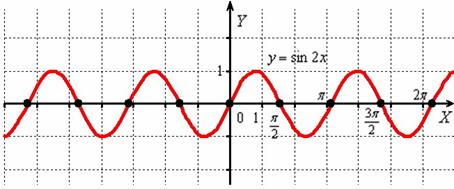
То есть, график функции  получается путём сжатия графика
получается путём сжатия графика  к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился:
к оси ординат в два раза. Логично, что период итоговой функции тоже уполовинился: 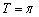
В целях самоконтроля можно взять 2-3 значения «икс» и устно либо на черновике выполнить подстановку:
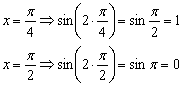
Пример 2
Построить график функции 
«Чёрная гармошка»  сжимается к оси
сжимается к оси 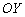 в 3 раза:
в 3 раза:

Итоговый график  проведён красным цветом.
проведён красным цветом.
Исходный период  косинуса закономерно уменьшается в три раза:
косинуса закономерно уменьшается в три раза:  (отграничен жёлтыми точками).
(отграничен жёлтыми точками).
|
|
|
Растяжение графика функции от оси ординат
Это противоположное действие, теперь баян не сжимается, а растягивается.
Случай имеет место, когда АРГУМЕНТ функции умножается на число  .
.
Правило: чтобы построить график функции 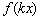 , где
, где  , нужно график функции
, нужно график функции 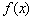 растянуть от оси
растянуть от оси 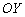 в
в  раз.
раз.
Продолжим мучить синус:
Пример 3
Построить график функции 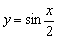
Берём в руки нашу «бесконечную гармошку»:
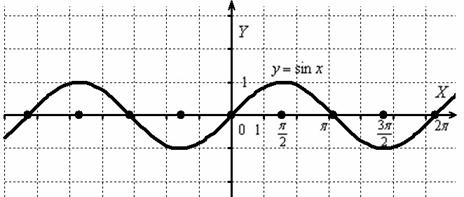
И растягиваем её от оси 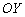 в 2 раза:
в 2 раза:

То есть, график функции 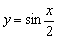 получается путём растяжения графика
получается путём растяжения графика  от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза:
от оси ординат в два раза. Период итоговой функции увеличивается в 2 раза:  , он толком даже не вместился на данный чертёж.
, он толком даже не вместился на данный чертёж.
Симметричное отображение графика функции относительно оси ординат
АРГУМЕНТ функции меняет знак.
Правило: чтобы построить график функции 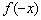 , нужно график
, нужно график 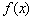 отобразить симметрично относительно оси
отобразить симметрично относительно оси 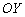 .
.
Пример 5
Построить график функции 
График функции  получается путём симметричного отображения графика
получается путём симметричного отображения графика 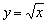 относительно оси ординат:
относительно оси ординат:
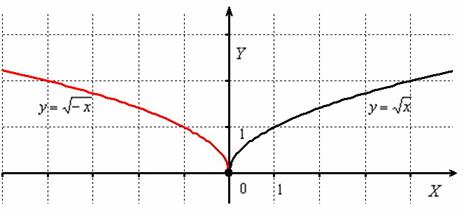
Как видите, всё просто.
Если при умножении аргумента на число 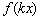 значение параметра
значение параметра 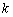 отрицательно и не равно минус единице, то построение выполняется в два шага.
отрицательно и не равно минус единице, то построение выполняется в два шага.
|
|
|
Растяжение (сжатие) графика ВДОЛЬ оси ординат.
Симметричное отображение графика относительно оси абсцисс
Структура второй части статьи будет очень похожа.
1) Если ФУНКЦИЯ 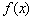 умножается на число
умножается на число 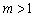 , то происходит растяжение её графика вдоль оси ординат.
, то происходит растяжение её графика вдоль оси ординат.
Правило: чтобы построить график функции  , где
, где 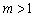 , нужно график функции
, нужно график функции 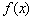 растянуть вдоль оси
растянуть вдоль оси 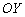 в
в  раз.
раз.
2) Если ФУНКЦИЯ умножается на число 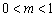 , то происходит сжатие её графика вдоль оси ординат.
, то происходит сжатие её графика вдоль оси ординат.
Правило: чтобы построить график функции  , где
, где 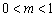 , нужно график функции
, нужно график функции 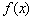 сжать вдоль оси
сжать вдоль оси 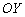 в
в 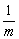 раз.
раз.
Пример 11
Построить графики функций 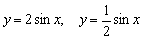 .
.
Берём синусоиду за макушку/пятки:

И вытягиваем её вдоль оси 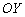 в 2 раза:
в 2 раза:

Период функции 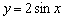 не изменился и составляет
не изменился и составляет  , а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается:
, а вот значения (все, кроме нулевых) увеличились по модулю в два раза, что логично – ведь функция умножается на 2, и область её значений удваивается: 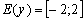 .
.
Теперь сожмём синусоиду вдоль оси 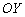 в 2 раза:
в 2 раза:
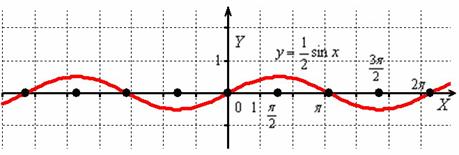
Аналогично, период  не изменился, но область значений функции «сплющилась» в два раза:
не изменился, но область значений функции «сплющилась» в два раза:  .
.
Нет, у меня нет какого-то пристрастного отношения к синусоиде, просто я хотел продемонстрировать, чем отличаются графики функций 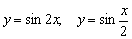 (Примеры №№1,3) от только что построенных собратьев
(Примеры №№1,3) от только что построенных собратьев 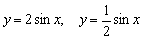 . Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
. Постарайтесь ещё раз проанализировать и качественнее понять эти элементарные случаи. Даже минимальные знания о преобразованиях графиков окажут вам неоценимую помощь в ходе решения других задач высшей математики!
|
|
|
Подготовка к контрольной.
Область определения функции, в которой есть дробь
Итак, нам надо найти все допустимые значения икса для какой-то конкретной функции. Самый широкий набор значений, как правило - это все действительные числа. От -∞ до+∞. Перебирать все возможные числа мы не будем, да...) В математике поступают по-другому. Работаем в два этапа.
На первом этапе ищем в функции операции, которые могут оказаться недопустимыми при каких-то значениях икса. Т.е. ищем потенциально опасные операции.
На втором этапе определяем иксы, которые не приводят к запретному действию в этих самых операциях. Это и будет область определения функции.
Если эти этапы не очень понятны, читаем дальше, на примерах всё куда яснее будет.
Что такое потенциально опасные операции? Это операции, в которых существуют принципиальные ограничения. Не пугайтесь, таких операций всего ничего и вы их прекрасно знаете). Перечисляю:
До 9-го класса включительно:
1. Деление. Нельзя делить на ноль.
2. Извлечение корня. Нельзя извлекать корни чётной степени из отрицательных чисел.
В выпускных классах и ВУЗах:
3. Логарифмы. Ограничения в логарифмах: если logab = c, то а>0, a≠1, b>0.
4. Тригонометрия. Ограничения в тригонометрии: значения углов, для которых тангенс и котангенс не существуют, ограничения на выражения под знаком арксинуса, арккосинуса.
Предположим, дана функция, содержащая некоторую дробь  . Как вы знаете, на ноль делить нельзя:
. Как вы знаете, на ноль делить нельзя:  , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
, поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде  и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби:
Пример 1
Найти область определения функции
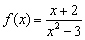
Решение: в числителе ничего особенного нет, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки:
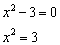
Полученное уравнение имеет два корня:  . Данные значения не входят в область определения функции. Действительно, подставьте
. Данные значения не входят в область определения функции. Действительно, подставьте 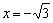 или
или  в функцию
в функцию 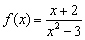 и вы увидите, что знаменатель обращается в ноль.
и вы увидите, что знаменатель обращается в ноль.
Ответ: область определения: 
Запись читается так: «область определения – все действительные числа за исключением множества, состоящего из значений  ». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
». Напоминаю, что значок обратного слеша в математике обозначает логическое вычитание, а фигурные скобки – множество. Ответ можно равносильно записать в виде объединения трёх интервалов:
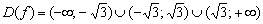 .
.
Пример 3
Найти область определения функции
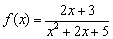
Решение: попытаемся найти точки, в которых знаменатель обращается в ноль. Для этого решим квадратное уравнение:

Дискриминант получился отрицательным, а значит, действительных корней нет, и наша функция определена на всей числовой оси.
Ответ: область определения: 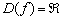
Определение.
Областью значений функции y = f(x) называется множество всех значений функции, которые она принимает при переборе всех x из области определения 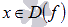 .
.
Пример.
Определите множество значений функции 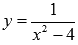 на интервале (-2; 2).
на интервале (-2; 2).
Решение.
Найдем точки экстремума функции, попадающие на промежуток (-2; 2):

Точка x = 0 является точкой максимума, так как производная меняет знак с плюса на минус при переходе через нее, а график функции от возрастания переходит к убыванию.

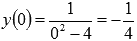 есть соответствующий максимум функции.
есть соответствующий максимум функции.
Выясним поведение функции при x стремящемся к -2 справа и при xстремящемся к 2 слева, то есть, найдем односторонние пределы:

Что мы получили: при изменении аргумента от -2 к нулю значения функции возрастают от минус бесконечности до минус одной четвертой (максимума функции при x = 0), при изменении аргумента от нуля к 2 значения функции убывают к минус бесконечности. Таким образом, множество значений функции на интервале (-2; 2) есть  .
.
Как найти область значения функции y=3x(квадрат)-6x +1
1 способ.
Найдем x0. x0=-b/(2a)=-(-6)/(2*3)=1
Найдем значение y при x=1.
y=3*1^2-6*1+1=3-6+1=-2.
Т.к. y=3x^2-6x+1 - это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
2 способ.
Найдем производную функции. y'=6x-6. Приравним производную функции к нулю.
6x-6=0. Найдем точки экстремума. 6x=6, x=1. Т.к. y=3x^2-6x+1 - это парабола, ветви направлены вверх, то x=1- это точка минимума. Найдем значение функции наданной точке. y=3*1^2-6*1+1=3-6+1=-2. Т.к. y=3x^2-6x+1 - это парабола, ветви направлены вверх, то область значений: [-2;+бесконечности)
P.S. Если вы ещё не прошли производную, воспользуйтесь первым способом.
Дата добавления: 2021-03-18; просмотров: 88; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
