Геометрический смысл определенного интеграла
Определенный интеграл 
численно равен площади криволинейной трапеции, ограниченной графиком функции y = f ( x ), осью Ох и прямыми x = a , x = b.
Вычисление площадей плоских фигур с помощью определенного интеграла
С помощью определенного интеграла можно вычислять площади плоских фигур, так как эта задача всегда сводится к вычислению площадей криволинейных трапеций.
Площадь всякой фигуры в прямоугольной системе координат может быть составлена из площадей криволинейных трапеций, прилегающих к оси Ох или к оси Оу.
Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
1. По условию задачи сделать схематический чертеж
2. Представить искомую площадь как сумму или разность площадей криволинейных трапеций. Из условия задачи и чертежа определяют пределы интегрирования для каждой составляющей криволинейной трапеции.
3. Записывают каждую функцию в виде y = f ( x ).
4. Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.
Рассмотрим несколько вариантов расположения фигур.
1). Пусть на отрезке [a ; b] функция f ( x ) принимает неотрицательные значения. Тогда график функции y = f ( x ) расположен над осью Ох.
Площадь такой фигуры вычисляется по формуле: S =
2). Пусть на отрезке [a ; b] неположительная непрерывная функция f ( x ). Тогда график функции y = f ( x ) расположен под осью Ох:
|
|
|
Площадь такой фигуры вычисляется по формуле: S = -
3)
Площадь такой фигуры вычисляется по формуле: S = 
4). Пусть на отрезке [a ; b] функция f ( x ) принимает как положительные, так и отрицательные значения. Тогда отрезок [a ; b] нужно разбить на такие части, в каждой из которых функция не изменяет знак, затем по приведенным выше формулам вычислить соответствующие этим частям площади и найденные площади сложить.
S1 =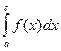 
S2 = - 
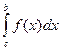Sф = S1 + S2
Пример. Вычислить площадь фигуры, ограниченной линиями: у2=9х, х=16, х=25, у=0.
Для любого значения 
функция 
принимает положительные значения, поэтому площадь заданной фигуры находится по формуле: S = 
= 
= 2(125-64) = 122 (кв.ед.)
Вычисление объема тела вращения
Рассмотрим кривую, заданную уравнением y = f ( x ). Предположим, что функция f ( x ) непрерывна на отрезке [a , b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.
y = f ( x )
x
|
|
|
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса 
, то объем тела вращения может быть легко найден по полученной выше формуле:
Дата добавления: 2021-03-18; просмотров: 63; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!