Экстремум функции двух переменных
Лекция 2.
1. Градиент. Производная по некоторому направлению 
в точке 
Производная неявно заданной ФНП
Экстремум функции двух переменных
Условный экстремум
Градиент. Производная по некоторому направлению в точке
1. Градиентом функции 
в точке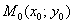 
называется вектор 
, отложенный от точки (0,0), который показывает направление искорость наискорейшего роста функции в данной точке.
Если совсем просто, то при ассоциации с горой , куда направлен градиент – там и самый крутой «подъём в гору»
Распространённые обозначения: 
либо 
, причём здесь уже нельзя записывать просто 
В нашем случае: 
.
Градиент в точке – этовектор , исходящий из начала координат в точку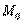 
Производная по некоторому направлению в точке 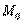– это по сути проекция вектора градиента в данной точке на данное направление:
Рассмотрим пример:
Дана функция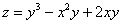 
, точка 
и вектор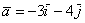 
. Требуется найти:
а) производную функции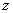 
в точке 
по направлению вектора 
;
б) градиент функции в данной точке.
Алгоритм решения:
а) Обозначим через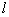 
исходящий из точки по направлению вектора 
луч и воспользуемся стандартной формулой:
( **)
Найдём частные производные первого порядка
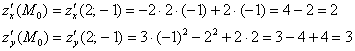
Далее, найдем единичный вектор, сонаправленный с вектором :
Нетрудно проверить, что сумма квадратов направляющих косинусов равна единице
Производная по направлению согласно формуле (**) равна:
|
|
|
Геометрическом смысле результата: отрицательный знак производной говорит об убывании функции в данном направлении
б) Найдем градиент функции в данной точке:
=(2;3)
Производная неявно заданной ФНП
Неявный вид функции двух переменных 
обозначают уравнением 
.
Пример1
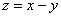– функция двух переменных в явном виде;
– та же функция, заданная неявно. (*)
Покажем общую схему решения на данном примере :
Найти частные производные 1-го порядка функции , не выражая z через х и у
Решение: Найдём 
. Возьмем частные производные по х от обеих частей равенства (*)
Далее пользуемся правилом 
:
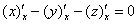
– это, очевидно, и есть наша частная производная 
, таким образом:
И на завершающем шаге выражаем результат:
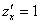
Аналогично с частной производной по «игрек»:
Ответ: 
Пример 2
Дана функция 
. Найти частные производные 1-го порядка по х и по у .
Решение:
По «икс»:
К правой части равенства необходимо применить правило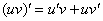 
:
При нахождении 
следует помнить, что z в квадрате является сложной функцией и к ней надо применить правило :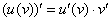 
. В данном случае внешняя функция – это степень, а внутренняя функция – это собственно функция «зет» В итоге получим :
|
|
|
Или :
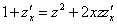
Теперь в левой части нужно собрать слагаемые, которые содержат производную, а справа – всё остальное:
Выносим за скобки и из полученного равенства находим :
Найдём частную производную по «игрек»:
Так как «икс» считается константой, то в правой части сразу выносим его за знак производной:
Второй способ решения:
Берём исходное уравнение , переносим все слагаемые в одну часть: 
и рассматриваем функцию трёх переменных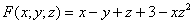 
. Тогда частные производные можно найти по следующим формулам:
(**)
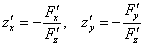Таким образом:
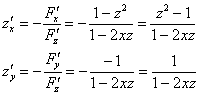
Экстремум функции двух переменных
Понятие экстремумов функции двух переменных вводится так же, как и для функции одной переменной
Определение.
Точками экстремума функции двух переменныхназываются точки минимума и максимума этой функции. Значения самой функции в точках экстремума называются экстремумами функции двух переменных.
Определение.
Точка М(x0, y0) называется точкой максимума функции двух переменныхz = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности.
Значение функции в точке максимума называется максимумом функции двух переменных.
|
|
|
Определение.
Точка М(x0, y0) называется точкой минимума функции двух переменных z = z(x, y), если значение функции в этой точке меньше чем в точках её окрестности. Значение функции в точке максимума называется минимумом функции двух переменных.
Теорема (необходимый признак экстремума функции двух переменных).
Если точка М(x0, y0) - точка экстремума функции двух переменных z = z(x, y), то первые частные производные функции (по "иксу" и по "игреку") в этой точке равны нулю или не существуют:
и
.
Определение.
Точки, в которой первые частные производные функции двух переменных равны нулю, называются стационарными точками.
Определение. Точки, в которой первые частные производные функции двух переменных равны нулю или не существуют, называются критическими точками.
Как и в случае с функцией одной переменной, необходимое условие существования экстремума функции двух переменных не является достаточным.
Каждая точка экстремума является критической точкой, но не каждая критическая точка является экстремумом.
Теорема
Достаточный признак существования экстремума функции двух переменных
В точке М существует экстремум функции двух переменных, если в окрестности этой точки полное приращение функции не меняет знак.
|
|
|
Так как в критической точке первый полный дифференциал равен нулю, то приращение функции определяет второй полный дифференциал
.
Локальный характер экстремумов функции двух переменных. Максимум функции двух переменных на каком-либо участке области определения функции не обязательно является максимумом во всей области определения , так же как и минимум на каком-либо участке не является минимумом во всей области определения. Пусть мы рассматриваем высоту волн на участке прибрежной области моря (участок меньше области). Тогда на этом участке мы можем зафиксировать (по-крайней мере, зрительно) наибольшую высоту волны. Но на другом участке, на котором ветер вызывает большую высоту волн, мы фиксируем минимальную высоту волны. Это к тому, что максимум высоты волны на первом участке может оказаться меньше, чем минимум высоты волны на втором участке. Поэтому, как и в случае экстремума функции одной переменной, необходимо уточнить это понятие и говорить об экстремумах как о локальных экстремумах функции двух переменных.
Дата добавления: 2021-03-18; просмотров: 115; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!