Понятие и геометрический смысл дифференциала
Уравнение касательной
Геометрический смысл производной: если к графику функции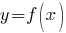 
в точке 
проведена касательная, то коэффициент наклона касательной (равный тангенсу угла между касательной и положительным направлением оси 
) равен производной функции в точке .
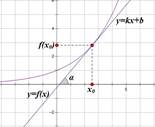
Возьмем на касательной произвольную точку с координатами 
:
И рассмотрим прямоугольный треугольник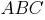 
:
В этом треугольнике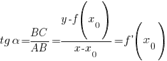 
Отсюда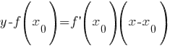 
Или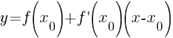 
Это и есть уравнение касательной, проведенной к графику функции 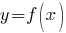в точке 
.
Чтобы написать уравнение касательной, нам достаточно знать уравнение функции и точку, в которой проведена касательная. Тогда мы сможем найт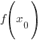и 
и 
.
Есть три основных типа задач на составление уравнения касательной.
1. Дана точка касания
2. Дан коэффициент наклона касательной, то есть значение производной функции 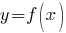в точке .
Рассмотрим каждый тип задач.
1 . Написать уравнение касательной к графику функции 
в точке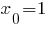 
.
а) Найдем значение функции в точке .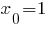 
.
б) Найдем значение производной в точке 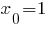. Сначала найдем производную функции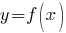
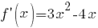
Подставим найденные значения в уравнение касательной:
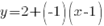Раскроем скобки в правой части уравнения. Получим: 
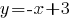Ответ: .
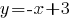2 . Найти абсциссы точек, в которых касательные к графику функции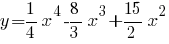 
параллельны оси абсцисс.
Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции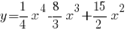 
в точках касания равно нулю.
|
|
|
а) Найдем производную функции 
. 
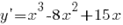
б) Приравняем производную к нулю и найдем значения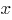 
, в которых касательная параллельна оси :
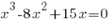
Приравняем каждый множитель к нулю, получим: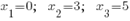 
Ответ: 0;3;5
3 . Написать уравнения касательных к графику функции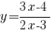 
, параллельных прямой 
Касательная параллельна прямой 
. Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Это второй тип задач на нахождение уравнения касательной.
Итак, у нас дана функция 
и значение производной в точке касания.
а) Найдем точки, в которых производная функции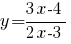 
равна -1.
Сначала найдем уравнение производной. Нам нужно найти производную дроби.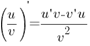 
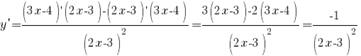Приравняем производную к числу -1.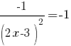 
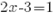или 
или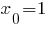
б) Найдем уравнение касательной к графику функции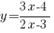 
в точке 
.
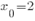Найдем значение функции в точке 
. 
(по условию)
Подставим эти значения в уравнение касательной: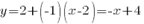 
.
б) Найдем уравнение касательной к графику функции 
в точке .
|
|
|
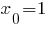Найдем значение функции в точке 
. 
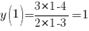
(по условию).
Подставим эти значения в уравнение касательной: 
. Ответ: 
Понятие и геометрический смысл дифференциала
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.
Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x; y), при изменении x (аргумента) на величину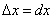 
(см. рисунок).
Дата добавления: 2021-03-18; просмотров: 53; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!