Плотность суммы двух непрерывных случайных величин
Пусть x и h — независимые случайные величины с плотностями 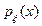 и
и  . Плотность случайной величины x + h вычисляется по формуле свертки
. Плотность случайной величины x + h вычисляется по формуле свертки

Задача 8. Пусть x и h — независимые случайные величины, распределенные по показательному закону с параметром  . Вычислить плотность суммы
. Вычислить плотность суммы  .
.
Решение. Так как x и h распределены по показательному закону с параметром  , то их плотности равны
, то их плотности равны

Следовательно,

Поэтому

Если x<0, то в этой формуле аргумент  у функции
у функции  отрицателен, и потому
отрицателен, и потому 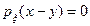 . Поэтому
. Поэтому  Если же
Если же 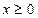 , то имеем:
, то имеем:
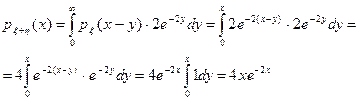
Таким образом, мы получили ответ:

Задачи для самостоятельного решения
Теоретические задачи.
- Найти плотности распределения: а) суммы; б) разности; в) произведения; г) частного двух случайных величин, имеющих равномерное распределение на [0; а].
- Случайная величина x имеет нормальное распределение с параметрами а и s2. Показать, что величина
 нормально распределена с параметрами 0 и 1.
нормально распределена с параметрами 0 и 1. - Случайные величины x1 и x2 независимы и имеют нормальные распределения с параметрами а1,
 и а2,
и а2, 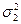 соответственно. Доказать, что x1 + x2 имеет нормальное распределение.
соответственно. Доказать, что x1 + x2 имеет нормальное распределение.
- Случайные величины x1, x2, ... xn распределены и независимы и имеют одинаковую функцию плотности распределения
 .
.
Найти функцию распределения и плотность распределения величин:
а) h1 = min {x1 , x2, ...xn} ; б) h(2) = max {x1,x2, ... xn }
- Случайные величины x1, x2, ... xn независимы и равномерно распределены на отрезке [а, b]. Найти функции распределения и функции плотности распределения величин
x(1) = min {x1,x2, ... xn} и x(2)= max{x1, x2, ...xn}.
Доказать, что М 
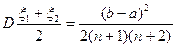 .
.
- Случайная величина распределена по закону Коши
 Найти: а) коэффициент а; б) функцию распределения; в) вероятность попадания на интервал (-1, 1). Показать, что математическое ожидание x не существует.
Найти: а) коэффициент а; б) функцию распределения; в) вероятность попадания на интервал (-1, 1). Показать, что математическое ожидание x не существует. - Случайная величина подчинена закону Лапласа с параметром l (l>0):
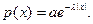 Найти коэффициент а; построить графики плотности распределения и функции распределения; найти Mx и Dx; найти вероятности событий {|x|<
Найти коэффициент а; построить графики плотности распределения и функции распределения; найти Mx и Dx; найти вероятности событий {|x|<  и {çxç<
и {çxç<  }.
}. - Случайная величина x подчинена закону Симпсона на отрезке [-а, а], т.е. график её плотности распределения имеет вид :
Написать формулу для плотности распределения, найти Мx и Dx.
Вычислительные задачи.
- Случайная точка А имеет в круге радиуса R равномерное распределение. Найти математическое ожидание и дисперсию расстояния r точки до центра круга. Показать, что величина r2 равномерно распределена на отрезке [0, R2].
- Плотность распределения случайной величины
 имеет вид:
имеет вид:

Вычислить константу C, функцию распределения F(x),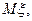 и вероятность
и вероятность 
- Плотность распределения случайной величины
 имеет вид:
имеет вид:

Вычислить константу C, функцию распределения F(x),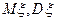 и вероятность
и вероятность 
- Плотность распределения случайной величины
 имеет вид:
имеет вид:

Вычислить константу C, функцию распределения F(x),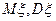 и вероятность
и вероятность 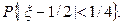
- Плотность распределения случайной величины
 имеет вид:
имеет вид: 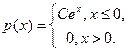
Вычислить константу C, функцию распределения F(x),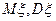 , дисперсию и вероятность
, дисперсию и вероятность 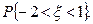
- Случайная величина
 имеет функцию распределения
имеет функцию распределения
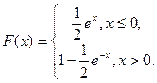
Вычислить плотность случайной величины, математическое ожидание, дисперсию и вероятность
- Проверить, что функция
 =
= 
может быть функцией распределения случайной величины. Найти числовые характеристики этой величины: Mx и Dx. - Случайная величина равномерно распределена не отрезке [2 ; 6]. Выписать плотность распределения. Найти функцию распределения. Найти вероятность попадания случайной величины на отрезок [2, 5] и на отрезок [5; 7].
- Плотность распределения x равна
 .
.
Найти постоянную с, плотность распределения h = 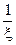 и вероятность
и вероятность
Р (0,25<h<0,64).
- Время безотказной работы ЭВМ распределено по показательному закону с параметром l = 0,05 (отказа в час), т.е. имеет функцию плотности
р(х) =  .
.
Решение определенной задачи требует безотказной работы машины в течение 15 минут. Если за время решения задачи произошел сбой, то ошибка обнаруживается только по окончании решения, и задача решается заново. Найти: а) вероятность того, что за время решения задачи не произойдет ни одного сбоя; б) среднее время, за которое будет решена задача.
- Стержень длины 24 см ломают на две части; будем считать, что точка излома распределена равномерно по всей длине стержня. Чему равна средняя длина большей части стержня?
- Отрезок длины 12 см случайным образом разрезается на две части. Точка разреза равномерно распределена по всей длине отрезка. Чему равна средняя длина малой части отрезка?
- Случайная величина
 равномерно распределена на отрезке [1,3]. Найти плотность распределения случайной величины
равномерно распределена на отрезке [1,3]. Найти плотность распределения случайной величины 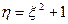 .
. - Случайная величина
 равномерно распределена на отрезке [-1,1]. Найти плотность распределения случайной величины
равномерно распределена на отрезке [-1,1]. Найти плотность распределения случайной величины 
- Случайная величина
 имеет функцию распределения
имеет функцию распределения

Найти функцию распределения случайной величины
- Случайная величина x имеет стандартное нормальное распределение (с параметрами а = 0 и s2 = 1). Найти плотность случайной величины
 .
. - Случайная величина x имеет показательное распределение с параметром l. Найти функции плотности распределения случайных величин:
а) h1= lx ; б) h2 =x2; в) h3=  г)
г) 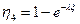 .
.
- Случайная величина x равномерно распределена на отрезке [0, 1]. Найти плотности распределения случайных величин:
а) h1 = 2x + 1; б) h2 =-ln(1-x); в) h3 =  .
.
- Показать, что если x имеет непрерывную функцию распределения
F(x) = P(x<x), то случайная величина h= F(x) имеет равномерное распределение на отрезке [0, 1].
- Найти функцию плотности и функцию распределения суммы двух независимых величин x и h c равномерными законами распределения на отрезках [1, 3] и [0; 1] соответственно.
- Случайные величины x и h независимы и равномерно распределены на отрезках [0, 2] и [3,4] соответственно. Вычислить плотность суммы x+h.
- Случайные величины x и h независимы и равномерно распределены на отрезках [0, 4] и [1,2] соответственно. Вычислить плотность суммы x+h.
- Случайные величины x и h независимы и равномерно распределены на отрезках [1, 3] и [2,4] соответственно. Вычислить плотность суммы x+h.
- Случайные величины независимы и имеют показательное распределение с плотностью
 . Найти плотность распределения их суммы.
. Найти плотность распределения их суммы. - Найти распределение суммы независимых случайных величин x и h, где x имеет равномерное на отрезке [0;1] распределение, а h имеет показательное распределение с параметром l.
- Найти Р
 , если x имеет: а) нормальное распределение с параметрами а и s2 ; б) показательное распределение с параметром l; в) равномерное распределение на отрезке [-1;1].
, если x имеет: а) нормальное распределение с параметрами а и s2 ; б) показательное распределение с параметром l; в) равномерное распределение на отрезке [-1;1]. - Совместное распределение x, h является равномерным в квадрате
К ={х, у): |х| +|у|£ 2}. Найти вероятность . Являются ли x и h независимыми?
. Являются ли x и h независимыми? - Пара случайных величин x и h равномерно распределена внутри треугольника K=
 . Вычислить плотность x и h. Являются ли эти случайные величины независимыми? Найти вероятность
. Вычислить плотность x и h. Являются ли эти случайные величины независимыми? Найти вероятность  .
. - Случайные величины x и h независимы и равномерно распределены на отрезках [0,1] и [-1,1]. Найти вероятность
 .
. - Двумерная случайная величина (x, h) равномерно распределена в квадрате с вершинами (2,0), (0,2), (-2, 0), (0,-2). Найти значение совместной функции распределения в точке (1, -1).
- Случайный вектор (x, h) равномерно распределен внутри круга радиуса 3 с центром в начале координат. Написать выражение для совместной плотности распределения. Определить, зависимы ли эти случайные величины. Вычислить вероятность
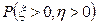 .
. - Пара случайных величин x и h равномерно распределена внутри трапеции с вершинами в точках (-6,0), (-3,4), (3,4), (6,0). Найти совместную плотность распределения для этой пары случайных величин и плотности составляющих. Зависимы ли x и h?
- Случайная пара (x, h) равномерно распределена внутри полукруга
 . Найти плотности x и h, исследовать вопрос об их зависимости.
. Найти плотности x и h, исследовать вопрос об их зависимости. - Совместная плотность двух случайных величин x и h равна
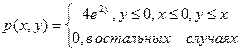 .
.
Найти плотности x, h. Исследовать вопрос о зависимости x и h. - Случайная пара (x, h) равномерно распределена на множестве
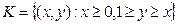 . Найти плотности x и h, исследовать вопрос об их зависимости. Найти М(xh).
. Найти плотности x и h, исследовать вопрос об их зависимости. Найти М(xh). - Случайные величины x и h независимы и распределены по показательному закону с параметром
 Найти
Найти 
Дата добавления: 2021-03-18; просмотров: 1784; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
