Координатный способ задания движения точки

Кинематика

1.к инематикой называется раздел механики, в котором изучается движение материальных тел в пространстве с геометрической точки зрения, вне связи с силами и массами, определяющим это движение.

Система отсчета - это система координат жестко связанная с телом по отношению к которому изучается движение. Отсчет времени ведется с некоторого начального момента (t = 0).

Кинематически задать движение или закон движения - это задать положение движущегося тела относительно системы отсчета в любой момент времени.

Основная задача кинематики состоит в том, чтобы зная закон движения данного тела определить все кинематические характеристики как самого тела, так и его точек (траекторию, скорости, ускорения и т.д.).

Традиционно изучение кинематики начинают с точки.

Траекторией называют линию, которую описывает движущаяся точка в пространстве (рис. 15). Траектории весьма разнообразны: они могут иметь вид прямой линии, окружности, эллипса, параболы (I), циклоиды (II) и других кривых. Длина траектории при движении материальной точки характеризует пройденный путь. При движении по прямой от одной точки пространства к другой пройденный путь равен расстоянию между точками, при движении по другим траекториям путь получается больше расстояния.

Величина пути и продолжительность движения во времени определяют скорость движения.

Скорость есть быстрота перемещения тел от одной точки пространства к другой, которая определяется величиной пути, проходимого за единицу времени.

Движение тела с постоянной скоростью называют равномерным, движение с переменной скоростью — переменным.

Величина, определяющая изменение скорости с течением времени, называется ускорением.

Способы задания движения точки

Как уже отмечалось, чтобы задать движение точки, нужно задать ее положение в выбранной системе отсчета в любой момент времени. Существуют три способа задания движения: 1) естественный, 2) координатный, 3) векторный.

1) Естественный способ задания движения.

Непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета, называется траекторией точки. В зависимости от вида траектории движение называют прямолинейным или криволинейным.

Пусть 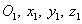- система отсчета; АВ - траектория; О - начало отсчета; - направление движения; S - криволинейная координата или расстояние вдоль дуги с соответствующим знаком (рис. 41 ).

Так как точка М движется вдоль траектории, то ее координата S будет изменяться со временем, то есть

S = f(t) (8.2.1)

Это и есть закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать: 1) траекторию точки. 2) начало отсчета на траектории с указанием направления движения ( ), 3) закон движения точки вдоль траектории в виде (8.2.1).

Здесь необходимо заметить, что S определяет положение точки на траектории, а не пройденный путь.

2) Координатный способ задания движения.

Положение точки по отношению к данной системе отсчета O,x,y,z можно определить с помощью координат x,y,z (рис. 42 ). При движении точки М вдоль траектории, с течением времени, координаты будут изменяться и чтобы задать закон движения точки, нужно задать зависимости:

Соотношения (8.2.2) представляют собой уравнения движения точки в декартовых прямоугольных координатах. Они представляют собой и параметрические уравнения траектории. Исключив параметр t, получим уравнение траектории через координаты.

3) Векторный способ задания движения.

Пусть задана система отсчета Oxyz (рис. 43 ).

Положение точки М в ней, в любой момент времени можно определить, задав вектор r из точки О в точку М. Такой вектор называется радиус-вектором точки М. С течением времени он изменяется, то есть

Это и есть закон движения точки в векторной форме. Годограф этого вектора определяет траекторию движения точки.

Определив все три закона движения, можно указать метод перехода от одного способа к другому.

Пусть уравнения движения заданы в форме (8.2.2), но

Задавая начальные условия: t = 0, S = 0 получаем

Это соотношение переводит закон движения из формы (8.2.2) в форму (8.2.1)

8.3.

Скорость точки

Скорость точки, являясь векторной величиной, определяет одну из основных кинематических характеристик движения точки. Введем понятие средней скорости.

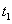Пусть в момент времени t точка находится в положении М и имеет радиус-вектор , а в момент времени , соответственно в 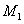и радиус-вектор 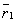(рис. 44 ).

Тогда за время 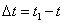точка переместится по траектории на вектор перемещения:

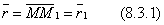
или

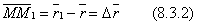
Отношение вектора перемещения точки к соответствующему промежутку времени называют средней по модулю и направлению скоростью точки за промежуток времени :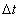

Направление вектора такое же как и 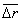, в сторону движения. Модуль скорости равен

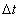Скоростью точки в данный момент t называется векторная величина , к которой стремится при , стремящемся к нулю

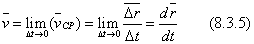
Так как предел секущей есть касательная, то вектор скорости точки в данный момент направлен по касательной к траектории в сторону движения.

Единица измерения скорости

8.4.

Ускорение точки

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в момент времени t точка занимает положение М и имеет скорость . В момент времени 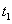она занимает положение 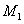и имеет скорость (рис. 45 ).

Тогда за промежуток времени 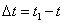она получит приращение скорости . Приращение скорости направлено в сторону вогнутости траектории.

Отношение приращения вектора скорости к приращению времени 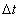определяет вектор среднего ускорения точки

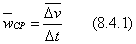
Вектор среднего ускорения направлен по линии действия . Ускорением точки в данный момент времени t называется векторная величина 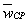, к которой стремится среднее ускорение при 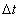, стремящемся к нулю:

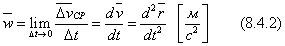
Вектор ускорения w лежит в соприкасающейся плоскости, то есть в плоскости проходящей через , когда 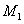стремится, в силу уменьшения 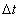, занять положение М, и направлен в сторону вогнутости кривой.

2. 1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из начала координат О в точку М (рис. 1).

Рис.1

При движении точки М вектор будет с течением времени изменяться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргумента :

Вектор скорости точки

Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки.

Известно, что при движении точки по прямой линии с постоянной скоростью, равномерно, скорость её определяется делением пройденного расстояния s на время: . При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится

Рис. 5

в момент времени t в положении М, определяемом радиусом-вектором , а в момент приходит в положение M₁определяемое вектором (рис.5). Тогда перемещение точки за промежуток времени определяется вектором который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что 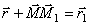; следовательно, .

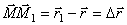Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени :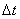

Скоростью точки в данный момент времени называется векторная величина 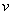, к которой стремится средняя скорость 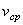при стремлении промежутка времени 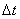к нулю:

, .

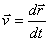Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.

Вектор ускорения точки

Пусть в некоторый момент времени движущаяся точка находится в положении М и имеет скорость 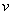, а в момент приходит в положение 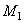и имеет скорость (рис. 6).

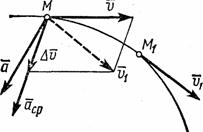
Рис.6

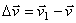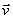Тогда за промежуток времени скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный , и построим параллелограмм, в котором диагональю будет , a одной из сторон . Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вогнутости траектории.

Отношение приращения вектора скорости к соответствующему промежутку времени 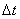определяет вектор среднего ускорения точки за этот промежуток времени:

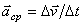Вектор среднего ускорения имеет то же направление, что и вектор , т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется векторная величина 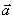, к которой стремится среднее ускорение при стремлении промежутка времени 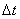к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.

Найдем, как располагается вектор 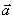по отношению к траектории точки. При прямолинейном движении вектор 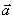направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения 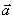, так же как и вектор , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор направлен в сторону вогнутости траектории и лежит в плоскости, проходящей через касательную к траектории в точке М и прямую, параллельную касательной в соседней точке M₁ (рис. 4). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.

Координатный способ задания движения точки

В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:

x=x(t)

y=y(t) (1.4)

z=z(t)

Рисунок 1.3

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

r(t)=i ⋅ x(t) ⊕ j ⋅ y(t) ⊕ k ⋅ z(t) (1.5)

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

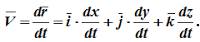
То есть:

Направление вектора скорости определяется с помощью направляющих косинусов:

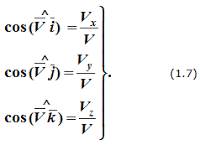
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

5. Аналогичны формулы для определения ускорения точки:

Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

6.Используется тогда, когда заранее известна траектория точки. Траекторию в этом случае считают криволинейной осью. На этой оси ( как и на любой координатной ) выделяют начало отсчета и положительное направление отсчета.

Положение точки на траектории определяется ее дуговой координатой s.

Зависимость дуговой координаты от времени,

которая в общем виде записывается в виде s = s(t),

Дата добавления: 2021-03-18; просмотров: 110; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 4 5 6 Следующая ⇒

Мы поможем в написании ваших работ!