Линейные однородные дифференциальные уравнения

Стр 1 из 3Следующая ⇒

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный архитектурно-строительный университет»

(ННГАСУ)

Методические указания и контрольные задания

По математике для студентов заочного обучения

Всех направлений

Часть 3

Нижний Новгород

ННГАСУ

2013

УДК 517.9

Методические указания и контрольные задания по математике для студентов заочного обучения всех направлений. Часть 3 [Текст]: метод. разраб. для студентов/ Нижегор. гос. архитектур.- строит. ун-т; сост. П.В. Столбов, Л.А. Протасова – Н.Новгород: ННГАСУ, 2013.- 61с.

Методические указания и контрольные задания по математике предназначены для студентов заочной формы обучения всех направлений.

Составители: П.В. Столбов, Л.А. Протасова

Дифференциальные уравнения первого порядка

В курсе математики средней школы изучались алгебраические уравнения, где неизвестными были числа. Сейчас мы переходим к рассмотрению так называемых дифференциальных уравнений, при решении которых находят неизвестные функции, удовлетворяющие заданным соотношениям, включающим операцию дифференцирования.

Рассмотрим для начала задачу о законе изменения скорости свободного падающего тела. Пусть тело массы 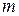падает с некоторой высоты. Учтем, что кроме силы тяжести, на него действует сила сопротивления воздуха. Запишем второй закон Ньютона

, (1.1)

предполагая, что сила сопротивления пропорциональна скорости в каждый момент времени 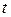с коэффициентом пропорциональности 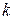. Уравнение (1.1), кроме неизвестной функции 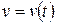, содержит еще и ее производную . Это и есть дифференциальное уравнение.

Дадим общие определения. Дифференциальным уравнением первого порядка называется уравнение

, (1.2)

связывающее независимую переменную и искомую функцию с ее первой производной . Если можно явно выразить через оставшиеся переменные уравнения (1.2), то оно приобретает вид

. (1.3)

Решением дифференциального уравнения (1.2) называется функция , которая при подстановке в уравнение (1.2) обращает его в тождество.

Можно убедиться, в частности, что функция

(1.4)

при любом значении постоянной 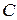удовлетворяет уравнению (1.1). Действительно, подставляя функцию (1.4) и ее производную в (1.1), получим тождество. Это означает, что функция вида (1.4) является решением уравнения (1.1).

Заметим, что мы нашли бесконечно много функций, удовлетворяющих дифференциальному уравнению (1.1) – каждому значению постоянной 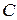соответствует свое решение вида (1.4).Множество функций 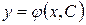, обращающих уравнение (1.3) в тождество, называют общим решением дифференциального уравнения (1.3). Запись общего решения содержит произвольную постоянную 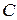. Заметим, что решение дифференциального уравнения может быть записано и в неявном виде .

Допустим, что в рассматриваемой задаче известна скорость тела в начальный момент времени . Обозначим её . Чтобы определить, как будет изменяться скорость тела в дальнейшем, выделим из найденного множества решений (1.4) только одно - то, которое соответствует начальному условию . При и из множества решений (1.4) получим 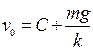, откуда 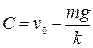. Подставляя найденное значение постоянной в (1.4), получим закон изменения скорости падающего тела при заданном начальном условии :

. (1.5)

Согласно последнему равенству, скорость падающего тела при будет стремиться к величине . Отсюда, в частности, можно найти нужный коэффициент сопротивления 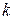(парашют), чтобы обеспечить приземление с допустимой скоростью. Функция (1.5) представляет собой так называемое частное решение уравнения (1.1), соответствующее начальному условию .

Частным решением уравнения (1.3) называется одна функция, удовлетворяющая самому уравнению и начальному условию. Задачу нахождения частного решения дифференциального уравнения (1.3), удовлетворяющего данному начальному условию , называют задачей Коши. Если правая часть уравнения (1.3) непрерывна в некоторой области, содержащей начальную точку , и имеет непрерывную в этой области частную производную 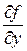, то задача Коши имеет единственное решение. При этих условиях частное решение получается из общего решения при конкретном значении произвольной постоянной .

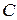Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения – интегральной кривой. Рассмотрим геометрическую интерпретацию решений уравнения (1.3) на конкретном примере. Пусть требуется найти частное решение дифференциального уравнения

, (1.6)

удовлетворяющего начальному условию

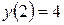. (1.7)

Непосредственной подстановкой убеждаемся, что функция вида

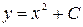(1.8)

обращает уравнение (1.6) в тождество. Она содержит произвольную постоянную 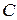и является общим решением уравнения (1.6). Построив в плоскости графики этих функций при различных значениях 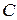. мы получим семейство парабол (см. рис.1).

Чтобы выделить из этого семейства интегральных кривых конкретную параболу, соответствующую условию (1.7), рассмотрим точку с координатами . Через нее проходит парабола семейства (1.8), для которой . Соответствующее решение является искомым частным решением.

Переходим к рассмотрению конкретных видов дифференциальных уравнений первого порядка и методов их решения.

Если правая часть дифференциального уравнения (1.3) может быть записана в виде произведения функций двух функций и 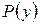, зависящих от переменных и соответственно, то есть , то уравнение называют дифференциальным уравнением с разделяющимися переменными.

Учитывая, что , перепишем последнее уравнение в виде

или .

Умножая обе части последнего уравнения на , получим

, (1.9)

в котором каждая из переменных и находится в той части уравнения, где ее дифференциал. Считая известной функцией от , равенство (1.9) можно рассматривать как равенство двух дифференциалов и интегрировать обе части уравнения (1.9). Полученные при этом функции и будут отличаться постоянным слагаемым: 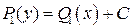. Мы записали соотношение, связывающее решение , независимую переменную и произвольную постоянную 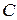, это соотношение и представляет собой общее решение дифференциального уравнения (1.3).

Уравнение с разделяющимися переменными, записанное исходно в дифференциальной форме

решается аналогично.

Решим для примера дифференциальное уравнение

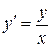. (1.10)

Функцию 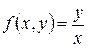в правой части уравнения можно представить в виде произведения и переписать уравнение (1.10):

или .

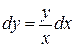Умножая обе части последнего уравнения на функцию , получим 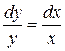. Интегрируя , находим , или 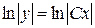, откуда 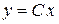– общее решение уравнения (1.10), где 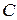– произвольная постоянная.

Решим далее задачу Коши: найдем решение уравнения

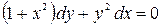, (1.11)

при условии, что

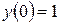. (1.12)

Дифференциальное уравнение (1.11) с разделяющимися переменными запишем в виде

Умножая обе части последнего уравнения на , разделим переменные: .

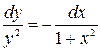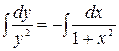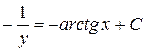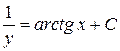Интегрируя , находим , или , где 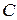– произвольная постоянная.

Итак, общее решение уравнения (1.11) имеет вид

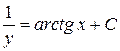Учет начального условия (1.12) дает , откуда 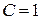. Следовательно, решение задачи Коши записывается в виде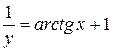

или .

Рассмотрим далее линейные дифференциальные уравнения первого порядка, которые, по определению, имеют вид

. (1.13)

Решение уравнения (1.13) будем искать в виде произведения

(1.14)

двух неизвестных функци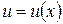й и 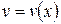, тогда

. (1.15)

Подставив в уравнение (1.13) вместо и равенства (1.14) и (1.15) соответственно, получим

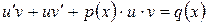или . (1.16)

Рассмотрение вместо одной неизвестной функции двух функций и 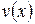дает возможность ввести для одной из них, в частности 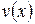, дополнительное условие, которое упростит уравнение. Оно состоит в требовании обращения выражения в нуль, то есть

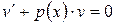. (1.17)

Уравнение (1.17) является дифференциальным уравнением с разделяющимися переменными и . Его запишем в виде или . Умножая обе части последнего уравнения на , разделяем переменные: 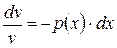. Интегрируем

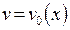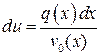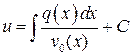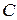и находим одно из решений уравнения (1.17), например, при постоянной . Это решение обозначим . Для второй неизвестной функции из (1.16) получим уравнение . Снова разделяем переменные и, интегрируя, находим , где – произвольная постоянная.

Подставляя найденные и 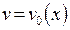в функцию (1.14), получаем решение уравнения (1.13) в виде .

Найдем для примера общее решение уравнения

(1.18)

В нем по условию 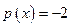, . Подставив в уравнение и 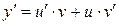, получим ,

или 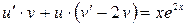. (1.19)

В качестве функции возьмем одно решение 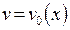уравнения 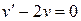при значении . Перепишем его в виде , разделим переменные и, интегрируя , находим . При получим . (1.20)

Подставим функцию (1.20) в (1.19), получим 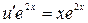или .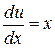

Снова разделяя переменные и интегрируя ,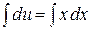

находим , (1.21)

где 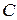– произвольная постоянная.

Подставляя найденные функции (1.20) и (1.21) в равенство , получим общее решение данного уравнения (1.18)

Линейные однородные дифференциальные уравнения

Второго порядка

Начнём с задачи из механики. Рассмотрим прямолинейное движение материальной точки массы 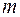по оси . Отклонение точки от положения равновесия будем определять функцией 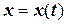. Пусть движение происходит под действием трёх сил: силы, притягивающей точку к началу координат и имеющей проекцию на ось , равную , силы сопротивления среды, которую считаем пропорциональной первой степени скорости и возмущающей силы, направленной по оси и равной в момент времени .

Применяя второй закон Ньютона к движущейся массе, получим

Разделим обе части уравнения на 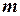и после введения новых обозначений , и приведем его к виду

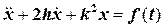. (2.1)

Полученное уравнение относится к классу так называемых линейных дифференциальных уравнений второго порядка, имеющих вид

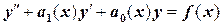. (2.2)

В них неизвестная функция и ее производные входят линейно. В качестве коэффициентов уравнения и 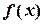могут рассматриваться любые функции, непрерывные в интервале . При этих условиях существует единственное решение уравнения (2.2), удовлетворяющее заданным начальным условиям .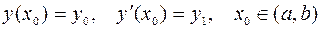

Если правая часть уравнения (2.2) равна нулю:

, (2.3)

то оно называется однородным, в противном случае (если ) – неоднородным.

Уравнение вида (2.2) служит математической моделью разнообразных колебательных физических процессов, то есть процессов, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например, качания маятника часов, переменный электрический ток и т.д. При колебательном движении маятника или груза на пружине изменяется координата центра масс, в случае переменного тока колеблются напряжение и сила тока. Физическая природа колебаний может быть разной, однако они описываются сходными характеристиками и уравнениями одинакового типа. Математические модели, сводящиеся к линейному дифференциальному уравнению второго порядка с постоянными коэффициентами, называют линейным осциллятором.

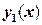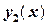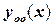Методика решений рассматриваемых уравнений базируется на следующем утверждении. Если и – два каких-либо непропорциональных друг другу решения уравнения (2.3), т.е. , то общее решение однородного дифференциального уравнения второго порядка имеет вид

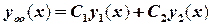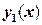где – произвольные постоянные. Следовательно, два любых непропорциональных решения однородного линейного дифференциального уравнения второго порядка формируют его общее решение. Однако нет общего метода отыскания функций и 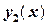. Их легко найти в случае, когда коэффициенты уравнения (2.3) являются числами. Обозначим их и :

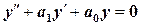. (2.4)

Такое уравнение называется линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его решения ищут в виде функций 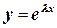. Рассмотрим, например, уравнение

Подставив в него функцию 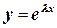, а также ее производные и , получим . Поскольку 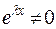, функция 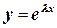будет решением, если – корень квадратного уравнения

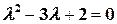которое называют характеристическим уравнением соответствующего дифференциального уравнения. Его корни и 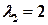, поэтому непропорциональные функци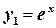и и формируют общее решение этого уравнения . В общем виде характеристическое уравнение дифференциального уравнения (2.4) имеет вид

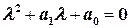. (2.5)

Если 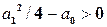, то уравнение (2.5) имеет два различных действительных корня 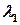и , которые определяются формулой

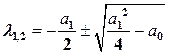При этом непропорциональные решения уравнения 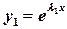и 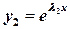формируют общее решение уравнения (2.4) в виде

Рассмотрим дифференциальное уравнение . Его характеристическое уравнение имеет два одинаковых корня 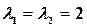(в таком случае говорят, что – корень кратности два). Одно из решений в этом случае нам известно: . Непосредственной подстановкой в уравнение можно убедиться, что функция 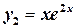также будет решением этого уравнения. Поскольку полученные функции непропорциональны, общее решение дифференциального уравнения получается в виде .

В целом можно сказать, что если выполняется условие , то характеристическое уравнение (2.5) имеет кратный корень , а общее решение однородного дифференциального уравнения второго порядка имеет вид .

Если же характеристическое уравнение (2.5) имеет комплексные корни , то можно убедиться, что функции и образуют пару непропорциональных решений уравнения (2.4), а его общее решение имеет вид

Такая ситуация возникает, если 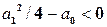, при этом , .

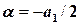Рассмотрим, например, дифференциальное уравнение . Его характеристическое уравнение 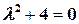имеет комплексные корни , а общее решение, тем самым, приобретает вид 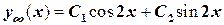. Для уравнения также составим характеристическое уравнение: 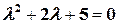. Его комплексные корни позволяют записать общее решение дифференциального уравнения в виде .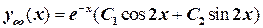

Вернёмся теперь к механическим колебаниям. Отсутствию возмущающей силы соответствует уравнение (2.1), в котором :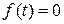

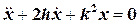. (2.6)

Такое уравнение называется уравнением свободных колебаний. Характеристическое уравнение в этом случае имеет вид

. (2.7)

Свободные колебания в среде без сопротивления описываются уравнением . В этом случае характеристическое уравнение 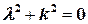имеет мнимые корни 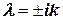, ему соответствует общее решение

Удобно привести записанное решение к другой форме, введя новые обозначения. Умножив и разделив на 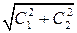, получим

Если положить

то общее решение приобретает вид

Оно описывает движение, которое называют гармоническим колебанием. Его график имеет вид:

Величину 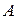называют амплитудойколебания, аргумент — фазойколебания, величину - начальной фазойколебания. Величина 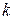представляет собой частотуколебания. Напомним, что . Периодколебания и частота k зависят только от массы системы и силы, притягивающей точку к началу координат. В задаче о движении тела, подвешенного на пружине, это означает зависимость от жесткости пружины.

Свободные колебания в среде с сопротивлением описываются уравнением (2.6). Если 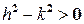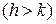, то характеристическое уравнение (2.7) имеет два различных действительных корня 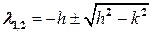. В модели движения груза на пружинке указанное условие означает, что сила сопротивления среды большесилы упругости пружины. Общее решение дифференциального уравнения в этом случае описывает апериодическое движение. Поскольку корни характеристического уравнения отрицательны, то с ростом координата 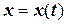стремится к нулю.

Характеристическое уравнение (2.7) имеет кратный корень , если 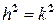, то есть . Для задачи о движении груза на пружине это означает, что сила сопротивления и сила упругости пружины «уравновешены» в смысле указанного равенства. Общее решение приобретает вид . При малых значениях основную «роль» играет первый множитель, линейный относительно , а затем с увеличением материальная точка будет стремиться к положению равновесия.

Если же 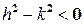(то есть - упругая сила пружины превосходит силу сопротивления среды в задаче о грузе на пружине), то характеристическое уравнение (2.7) имеет комплексные корни .

Общее решение

описывает затухающие гармонические колебания с периодом , частотой и амплитудой , убывающей с увеличением . Вид графика решения:

Проанализировав полученные результаты, можно сказать, что наличие сопротивления видоизменяет характер колебаний: пока сопротивление сравнительно невелико , движения остаются периодическими, затухая с увеличением , при большом сопротивлении среды движения становятся апериодическими.

Дата добавления: 2021-03-18; просмотров: 51; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!