Вычисление НОД. Алгоритм Евклида
ГЛАВА 3. ДЕЛИМОСТЬ ЧИСЕЛ. ДЕЛЕНИЕ С ОСТАТКОМ. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ.
Делимость чисел
Известно, что сумма, разность и произведение целых чисел является целым числом. Этот факт принято называть замкнутостью множества целых чисел по отношению к действиям сложения, вычитания и умножения. По отношению к действию деления множество целых чисел, очевидно, замкнутым не является. Например, результат деления числа 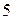 на число
на число  целым не является. Однако в некоторых случаях результат деления целого числа на целое число также является целым. Введем следующее определение.
целым не является. Однако в некоторых случаях результат деления целого числа на целое число также является целым. Введем следующее определение.
Определение 1.1. Пусть  и
и  – целые числа. Говорят, что число
– целые числа. Говорят, что число  делится на число
делится на число  , если найдется такое целое число
, если найдется такое целое число  , что
, что  . При этом число
. При этом число  называют делимым, число
называют делимым, число  – делителем, а число
– делителем, а число  – частным.
– частным.
Факт делимости числа  на число
на число  обозначают
обозначают 

 . Также говорят, что
. Также говорят, что  кратно
кратно  .
.
Примеры. 1) 65  13, так как
13, так как  ;
;
2) 0  3, так как
3, так как 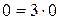 ;
;
3) 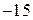
 5, так как
5, так как  .
.

 В определении делимости ничего не говорится о том, сколько различных значений может иметь частное от деления
В определении делимости ничего не говорится о том, сколько различных значений может иметь частное от деления  на
на  . Предположим, что при делении
. Предположим, что при делении  на
на  могут быть различные частные. Это значит, что существуют такие различные целые числа
могут быть различные частные. Это значит, что существуют такие различные целые числа  и
и  , что выполняются равенства
, что выполняются равенства  и
и 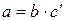 . Тогда
. Тогда
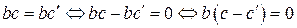 .
.
Если 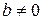 , то
, то  . Значит, в случае, когда делитель отличен от нуля, частное единственно.
. Значит, в случае, когда делитель отличен от нуля, частное единственно.
|
|
|
Если  , то, очевидно,
, то, очевидно,  , и равенство
, и равенство  выполняется для любого значения
выполняется для любого значения  .Таким образом, на
.Таким образом, на 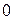 делится только
делится только 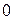 , а частное от такого деления неопределенно (может быть любым числом).
, а частное от такого деления неопределенно (может быть любым числом).
В дальнейшем, говоря о делении, всегда будем предполагать, что делитель отличен от 0.
Свойства делимости
1. Если 

 , то
, то 
 (–
(–  ); (–
); (–  )
) 
 ; (–
; (–  )
) 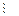 (–
(–  ).
).
Доказательство. Пусть 

 , это значит, что существует такое целое число
, это значит, что существует такое целое число  , что
, что  . Тогда
. Тогда  , причем число
, причем число  также является целым. Следовательно, по определению делимости
также является целым. Следовательно, по определению делимости 
 (–
(–  ). Остальные утверждения доказываются аналогично.
). Остальные утверждения доказываются аналогично.
2. Если 

 и
и 

 , то
, то 

 .
.
Доказательство. 



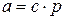 , где
, где  ;
; 



 , где
, где  . Тогда
. Тогда 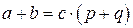 . Число
. Число  – целое, значит,
– целое, значит, 

 .
.
Следствие. Из свойств 1 и 2 непосредственно следует, что если 

 и
и 

 , то
, то 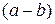

 .
.
3. Если 

 и
и  , то
, то 

 .
.
Доказательство. 



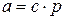 , где
, где  . Умножим обе части последнего равенства на
. Умножим обе части последнего равенства на  , получим
, получим 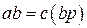 . Число
. Число  – целое, значит,
– целое, значит, 

 .
.
4. Если 

 и
и  не делится на
не делится на  , то
, то 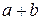 не делится на
не делится на  .
.
Доказательство. Предположим, что данное утверждение неверно: 

 . Это значит, что
. Это значит, что  , где
, где  . Тогда
. Тогда  . Но
. Но 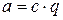 , где
, где  . Следовательно,
. Следовательно,  . Поскольку
. Поскольку  , получим, что
, получим, что 

 , что противоречит условию. Полученное противоречие доказывает, что сделанное нами предположение неверно.
, что противоречит условию. Полученное противоречие доказывает, что сделанное нами предположение неверно.
5. Если  и
и 

 , то
, то  .
.
Доказательство. 


 , где
, где  , причем
, причем 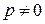 . Тогда
. Тогда  . Но
. Но  , значит
, значит  .
.
|
|
|
Следствие 1. Если 

 , то либо
, то либо  , либо
, либо  .
.
Доказательство. Если 

 , то по свойству 5 справедливо неравенство
, то по свойству 5 справедливо неравенство  . При этом
. При этом  – целое число, отличное от 0. Следовательно,
– целое число, отличное от 0. Следовательно,  , а это и значит, что либо
, а это и значит, что либо  , либо
, либо  .
.
Следствие 2. Если 

 и
и 

 , то либо
, то либо 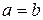 , либо
, либо 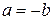 .
.
Доказательство. Если 

 и
и 

 , то по свойству 5 справедливы неравенства
, то по свойству 5 справедливы неравенства  и
и  . Одновременное выполнение этих неравенств может быть только в случае, когда
. Одновременное выполнение этих неравенств может быть только в случае, когда  , что и означает, что либо
, что и означает, что либо 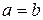 , либо
, либо 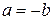 .
.
Отметим, что отношение делимости является бинарным отношением на множестве  . Рассмотрим его свойства делимости как бинарного отношения.
. Рассмотрим его свойства делимости как бинарного отношения.
1. Рефлексивность. Очевидно, что 

 . Значит, отношение делимости рефлексивно.
. Значит, отношение делимости рефлексивно.
2. Проверим, обладает ли отношение делимости каким-либо из свойств симметричности, антисимметричности или асимметричности. По следствию 2 к свойству 5, если 

 и
и 

 , то либо
, то либо 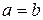 , либо
, либо 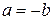 . Следовательно, ни одним из перечисленных свойств данное бинарное отношение не обладает.
. Следовательно, ни одним из перечисленных свойств данное бинарное отношение не обладает.
Заметим, что если рассмотреть отношение делимости на множестве натуральных чисел N, то окажется, что это отношение обладает свойством антисимметричности. Действительно, в этом случае следствие 2 к свойству 5 примет вид: если 

 и
и 

 , то
, то 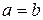 (поскольку на множестве N равенство
(поскольку на множестве N равенство 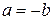 невыполнимо).
невыполнимо).
|
|
|
3. Транзитивность отношения делимости означает, что если 

 и
и 

 , то
, то 

 . Докажем, что отношение делимости транзитивно. Действительно,
. Докажем, что отношение делимости транзитивно. Действительно,




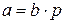 , где
, где  ;
;




 , где
, где  .
.
Следовательно,  , при этом, очевидно,
, при этом, очевидно,  , а это и означает, что
, а это и означает, что 

 .
.
Таким образом, на множестве натуральных чисел N отношение делимости является отношением нестрогого порядка.
Деление с остатком
Определение 2.1. Пусть  и
и  – целые числа. Разделить число
– целые числа. Разделить число  на число
на число  с остатком, значит найти такие целые числа
с остатком, значит найти такие целые числа  и
и  , что выполняются условия:
, что выполняются условия:
1) 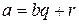
2) 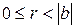 .
.
При этом  называется неполным частным, а
называется неполным частным, а  – остатком от деления
– остатком от деления  на
на  .
.
Примеры. 1) Разделить 5 на 3 с остатком. В соответствии с определением представим число 5 в виде: 5=3  1+2. Здесь
1+2. Здесь 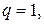
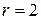 . Условие 2 из определения, очевидно, выполняется.
. Условие 2 из определения, очевидно, выполняется.
2) Разделить (–5) на 3 с остатком: (–5)=3  (–2)+1. Здесь
(–2)+1. Здесь 
 ;
;  .
.
3) Разделить 5 на (–3) с остатком: 5=(–3)  (–1)+2. Здесь
(–1)+2. Здесь 
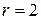 ;
; 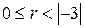 .
.
4) Разделить (–5) на (–3) с остатком: (–5)=(–3)  2+1. Здесь
2+1. Здесь 
 ;
; 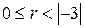 .
.
Теорема 2.1. Пусть 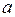 и
и  – целые числа, причем
– целые числа, причем 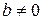 . Число
. Число 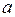 всегда можно разделить на число
всегда можно разделить на число  с остатком, причем единственным образом.
с остатком, причем единственным образом.
Доказательство. Рассмотрим случай, когда 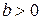 ,
,
1) Пусть 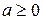 . Рассмотрим последовательность чисел:
. Рассмотрим последовательность чисел: 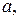
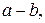
 … Поскольку
… Поскольку 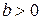 , начиная с некоторого члена этой последовательности, все члены будут отрицательными. Пусть последним из неотрицательных членов будет число
, начиная с некоторого члена этой последовательности, все члены будут отрицательными. Пусть последним из неотрицательных членов будет число  . Положим
. Положим 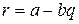 . Тогда
. Тогда 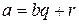 , где
, где 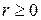 . Докажем, что
. Докажем, что  . Запишем это неравенство в виде
. Запишем это неравенство в виде 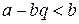 . Если бы это неравенство не выполнялось, то
. Если бы это неравенство не выполнялось, то  . Последние неравенство противоречит тому, что
. Последние неравенство противоречит тому, что  является последним неотрицательным числом в последовательности. Таким образом мы доказали, что число
является последним неотрицательным числом в последовательности. Таким образом мы доказали, что число 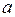 делится на
делится на  с остатком.
с остатком.
|
|
|
2) Пусть  . Рассмотрим последовательность чисел:
. Рассмотрим последовательность чисел: 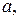

 … Поскольку
… Поскольку 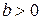 , начиная с некоторого члена этой последовательности, все члены будут положительными. Пусть
, начиная с некоторого члена этой последовательности, все члены будут положительными. Пусть  – первое неотрицательное число в этой последовательности. Положим
– первое неотрицательное число в этой последовательности. Положим  . Тогда
. Тогда 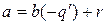 , где
, где 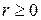 . Докажем, что
. Докажем, что  . Запишем это неравенство в виде
. Запишем это неравенство в виде  . Предположим, что неравенство не выполняется, тогда
. Предположим, что неравенство не выполняется, тогда 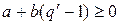 . Но
. Но  – первое неотрицательное число в последовательности. Полученное противоречие доказывает, что сделанное нами предположение неверно. Положим
– первое неотрицательное число в последовательности. Полученное противоречие доказывает, что сделанное нами предположение неверно. Положим  , тогда
, тогда 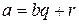 .
.
Таким образом, мы доказали возможность деления с остатком для любых целых чисел 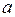 и целых положительных чисел
и целых положительных чисел  .
.
Случай, когда 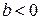 , рассматривается аналогично.
, рассматривается аналогично.
3) Докажем, что при делении одного целого числа на другое неполное частное и остаток определяются единственным образом. Пусть 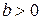 .
.
Предположим, что  и
и 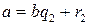 , где
, где  и
и  . Тогда
. Тогда  . Поскольку
. Поскольку  , из последнего равенства следует, что
, из последнего равенства следует, что 

 . По свойству 5 делимости чисел, если
. По свойству 5 делимости чисел, если  , то
, то 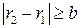 , что невозможно в силу условий
, что невозможно в силу условий  и
и  . Следовательно,
. Следовательно,  , а, значит, и
, а, значит, и 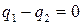 . Случай, когда
. Случай, когда 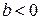 , рассматривается аналогично.
, рассматривается аналогично.
Наибольший общий делитель
Определение 3.1. Рассмотрим 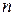 целых чисел
целых чисел 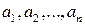 и целое число
и целое число  , причем
, причем 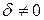 . Число
. Число  называется общим делителем чисел
называется общим делителем чисел 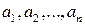 , если каждое из этих чисел делится на
, если каждое из этих чисел делится на  :
: 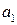

 ,
, 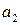

 ,…,
,…, 

 .
.
Определение 3.2. Рассмотрим 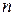 целых чисел
целых чисел 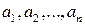 и целое число
и целое число  . Число
. Число  называется наибольшим общим делителем чисел (НОД) чисел
называется наибольшим общим делителем чисел (НОД) чисел 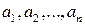 , если
, если
1)  является общим делителем чисел
является общим делителем чисел 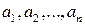 ,
,
2)  делится на любой из общих делителей чисел
делится на любой из общих делителей чисел 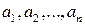 .
.
НОД чисел 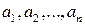 обозначают
обозначают  .
.
Определение 3.3. Если 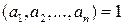 , то числа
, то числа 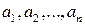 называются взаимно простыми.
называются взаимно простыми.
Свойства НОД
Теорема 3.1. НОД чисел 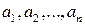 определен однозначно с точностью до знака, т. е., если числа
определен однозначно с точностью до знака, т. е., если числа  и
и  – наибольшие общие делители чисел
– наибольшие общие делители чисел 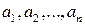 , то либо
, то либо  , либо
, либо  .
.
Доказательство. Из определения НОД следует, что 

 и
и 

 , поскольку оба этих числа являются общими делителями чисел
, поскольку оба этих числа являются общими делителями чисел 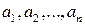 . Тогда по следствию 2 к свойству 5 делимости чисел либо
. Тогда по следствию 2 к свойству 5 делимости чисел либо  , либо
, либо  .
.
Замечание. По теореме 3.1. каждая совокупность целых чисел обладает ровно двумя НОД, отличающимися друг от друга только знаками. Поэтому можно рассматривать только случай, когда НОД чисел положителен. Далее будем считать, что  .
.
Теорема 3.2. Пусть  (т. е. число
(т. е. число  является наибольшим общим делителем чисел
является наибольшим общим делителем чисел 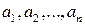 ). Тогда число
). Тогда число  является наибольшим по величине общим делителем этих чисел.
является наибольшим по величине общим делителем этих чисел.
Доказательство. Пусть  – общий делитель чисел
– общий делитель чисел 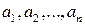 . Тогда из определения НОД следует, что
. Тогда из определения НОД следует, что 

 . По свойству 5 делимости чисел
. По свойству 5 делимости чисел 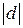

 . Мы условились считать, что НОД чисел положителен, следовательно,
. Мы условились считать, что НОД чисел положителен, следовательно, 

 . Учитывая, что
. Учитывая, что  , получим требуемое утверждение.
, получим требуемое утверждение.
Теорема 3.3. Пусть 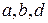 – целые числа. Для того, чтобы число
– целые числа. Для того, чтобы число  было НОД чисел
было НОД чисел  и
и  необходимо и достаточно, чтобы существовали такие взаимно простые числа
необходимо и достаточно, чтобы существовали такие взаимно простые числа  и
и  , что
, что  .
.
Доказательство. Необходимость. Пусть 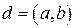 . Докажем, что существуют такие взаимно простые числа
. Докажем, что существуют такие взаимно простые числа  и
и  , что
, что  . Поскольку числа
. Поскольку числа  и
и  делятся на
делятся на  , имеем
, имеем  . Докажем, что числа
. Докажем, что числа  и
и  – искомые, т. е.
– искомые, т. е. 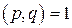 . Предположим, что это утверждение неверно, это значит, что
. Предположим, что это утверждение неверно, это значит, что 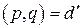 , где
, где 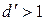 . Тогда
. Тогда  , где
, где  – целые числа. Следовательно,
– целые числа. Следовательно,  . Значит,
. Значит, 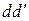 – общий делитель чисел
– общий делитель чисел  и
и  , причем
, причем  . Получили, что число
. Получили, что число  не является наибольшим общим делителем чисел
не является наибольшим общим делителем чисел  и
и  , что противоречит условию. Следовательно, сделанное нами предположение неверно, что и доказывает требуемое утверждение.
, что противоречит условию. Следовательно, сделанное нами предположение неверно, что и доказывает требуемое утверждение.
Достаточность. Пусть  , где
, где 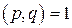 . Докажем, что
. Докажем, что 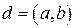 . Из условия утверждения следует, что
. Из условия утверждения следует, что 

 и
и 

 , следовательно,
, следовательно,  – делитель чисел
– делитель чисел  и
и  .
.
Предположим, что  – не является наибольшим общим делителем чисел
– не является наибольшим общим делителем чисел  и
и  . Пусть
. Пусть 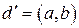 . Тогда
. Тогда 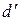

 . Это значит, что
. Это значит, что 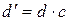 , где
, где  – целое число, причем
– целое число, причем 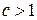 . Из определения НОД получим, что
. Из определения НОД получим, что  . Тогда
. Тогда 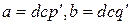 . Из единственности частного следует, что
. Из единственности частного следует, что  . Значит, числа
. Значит, числа  и
и  не являются взаимно простыми, что противоречит сделанному нами предположению. Полученное противоречие доказывает справедливость утверждения.
не являются взаимно простыми, что противоречит сделанному нами предположению. Полученное противоречие доказывает справедливость утверждения.
Вычисление НОД. Алгоритм Евклида
Алгоритм Евклида дает возможность вычислить наибольший общий делитель для любых двух целых чисел. Для описания алгоритма рассмотрим следующие две леммы.
Лемма 1. Если 

 , то
, то  .
.
Доказательство. Очевидно, что  – общий делитель чисел
– общий делитель чисел  и
и  , поскольку
, поскольку 

 и
и 

 . Пусть
. Пусть  – общий делитель чисел
– общий делитель чисел  и
и  , тогда
, тогда 

 . Значит,
. Значит,  – наибольший общий делитель чисел
– наибольший общий делитель чисел  и
и  по определению.
по определению.
Лемма 2. Пусть 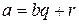 , причем числа
, причем числа 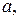
 и
и  отличны от 0 и
отличны от 0 и  . Тогда
. Тогда 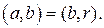
Доказательство. Пусть 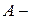 множество общих делителей чисел
множество общих делителей чисел  и
и  , а
, а  множество общих делителей чисел
множество общих делителей чисел  и
и  . Докажем, что
. Докажем, что 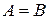 .
.
Пусть 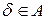 , это значит, что
, это значит, что 

 и
и 

 . Тогда по свойству делимости
. Тогда по свойству делимости 

 . Тогда,
. Тогда, 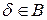 , следовательно,
, следовательно, 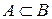 . Аналогично докажем, что
. Аналогично докажем, что 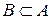 . Из определения равенства двух множеств получим, что
. Из определения равенства двух множеств получим, что 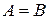 .
.
Если два числовых множества совпадают, то совпадают их наибольшие по величине элементы, что и доказывает лемму.
Сформулируем теперь алгоритм Евклида.
Рассмотрим два целых числа  и
и  . Пусть
. Пусть  Требуется найти наибольший общий делитель чисел
Требуется найти наибольший общий делитель чисел  и
и  .
.
Шаг 1. Разделим  на
на  . Если
. Если 

 , то по лемме 1 получим, что
, то по лемме 1 получим, что  .
.
Если число  не делится на
не делится на  , то
, то 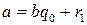 , где
, где  . Тогда по лемме 2
. Тогда по лемме 2 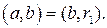
Шаг 2. Разделим  на
на 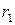 . Если
. Если 

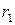 , то
, то  (по лемме 1). Тогда
(по лемме 1). Тогда 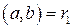 .
.
Если  не делится на
не делится на 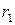 , то
, то 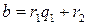 , где
, где 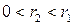 . Тогда по лемме 2
. Тогда по лемме 2 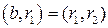 , а значит, справедливо и
, а значит, справедливо и 
Продолжая процесс деления, получим последовательность остатков – убывающую последовательность целых неотрицательных чисел, вычисляемых по следующим рекуррентным формулам:  .
.
Поскольку такая последовательность не может иметь бесконечно много членов, на некотором шаге очередной остаток окажется равным нулю. Тогда последний, отличный от нуля остаток и есть НОД чисел  и
и  .
.
Пример. Найдем НОД чисел  и
и 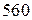 . Для этого разделим
. Для этого разделим  на
на 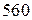 , получим
, получим  . Таким образом, первый полученный остаток
. Таким образом, первый полученный остаток  .
.
Далее, разделим 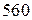 на
на 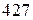 , получим
, получим 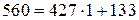 , при этом
, при этом 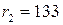 . Продолжим процесс деления:
. Продолжим процесс деления:
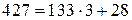 ,
,  ;
;
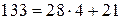 ,
,  ;
;
 ,
, 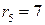 ;
;
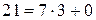 ,
, 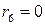 .
.
Таким образом, последний отличный от 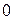 остаток равен
остаток равен 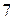 , это и есть наибольший общий делитель чисел
, это и есть наибольший общий делитель чисел  и
и 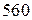 .
.
В следующей теореме утверждается, что наибольший общий делитель двух чисел можно представить в виде линейной комбинации этих чисел с целыми коэффициентами.
Теорема 4.1. (линейное представление НОД )
Рассмотрим два целых числа  и
и  . Пусть
. Пусть 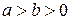 ,
, 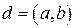 . Тогда найдутся такие целые числа
. Тогда найдутся такие целые числа 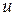 и
и 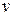 , что
, что  .
.
Доказательство. Докажем, что каждый из остатков  , полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел
, полученных в процессе выполнения алгоритма Евклида, можно представить в виде линейной комбинации чисел  и
и  с целыми коэффициентами. Тогда это утверждение будет справедливо в частности и для последнего, отличного от
с целыми коэффициентами. Тогда это утверждение будет справедливо в частности и для последнего, отличного от 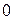 остатка, равного
остатка, равного 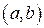 . Будем доказывать это утверждение методом математической индукции.
. Будем доказывать это утверждение методом математической индукции.
База индукции.
Пусть 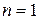 . Имеем
. Имеем 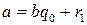 , тогда
, тогда  . Получили, что остаток
. Получили, что остаток 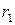 можно представить в виде линейной комбинации чисел
можно представить в виде линейной комбинации чисел  и
и  с целыми коэффициентами
с целыми коэффициентами 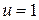 и
и  .
.
Индукционный переход.
Пусть утверждение справедливо для всех натуральных чисел 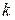 , не превосходящих
, не превосходящих 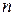 :
:  , при
, при  . Докажем, что это утверждение справедливо также для
. Докажем, что это утверждение справедливо также для 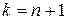 .
.
Из алгоритма Евклида следует, что


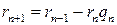 .
.
По индукционному предположению
 и
и  .
.
Следовательно,  .
.
Положим 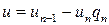 и
и  . Тогда
. Тогда  , что и требовалось установить.
, что и требовалось установить.
Пример. В предыдущем примере был найден НОД чисел  и
и 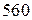 :
:  . Найдем его линейное представление:
. Найдем его линейное представление:
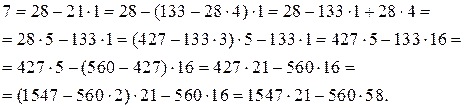
Итак, получили, что 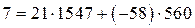 , т. е. представили НОД чисел
, т. е. представили НОД чисел  и
и 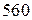 в виде их линейной комбинации с целыми коэффициентами.
в виде их линейной комбинации с целыми коэффициентами.
Взаимно простые числа
Определение 5.1. Целые числа 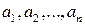 называются взаимно простыми, если их НОД равен
называются взаимно простыми, если их НОД равен  :
:

Примеры.
1. Числа 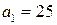 и
и  – взаимно простые.
– взаимно простые.
2. Числа 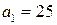 и
и 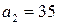 – не взаимно простые, так как
– не взаимно простые, так как 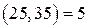 .
.
Следующая теорема устанавливает необходимое и достаточное условие взаимной простоты чисел.
Теорема 5.1 (признак взаимной простоты чисел). Для того, чтобы числа  и
и  были взаимно простыми, необходимо и достаточно, чтобы нашлись такие целые числа
были взаимно простыми, необходимо и достаточно, чтобы нашлись такие целые числа 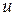 и
и 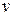 , что
, что 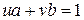 .
.
Доказательство. 1. Необходимость. Пусть числа  и
и  взаимно просты, то есть
взаимно просты, то есть 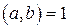 . Тогда по теореме о линейном представлении НОД найдутся такие целые числа
. Тогда по теореме о линейном представлении НОД найдутся такие целые числа 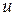 и
и 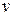 , что
, что 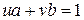 .
.
2. Достаточность. Пусть справедливо утверждение 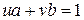 , где
, где 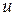 и
и 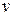 – целые числа. Докажем, что
– целые числа. Докажем, что 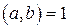 . Предположим, что числа
. Предположим, что числа  и
и  не являются взаимно простыми:
не являются взаимно простыми:  , причем
, причем 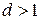 . Тогда
. Тогда 

 и
и 

 , и по свойству делимости
, и по свойству делимости 

 . Значит,
. Значит, 

 , следовательно,
, следовательно,  . Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо
. Полученное противоречие доказывает, что сделанное нами предположение неверно, и, тем самым, справедливо 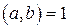 .
.
Следствие 1. Если числа  и
и  взаимно просты, причем
взаимно просты, причем 

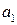 и
и 

 , то числа
, то числа 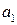 и
и  также взаимно просты.
также взаимно просты.
Доказательство. По теореме из взаимной простоты чисел  и
и  следует, что найдутся такие целые числа
следует, что найдутся такие целые числа 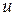 и
и 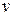 , что
, что 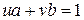 . Из определения делимости
. Из определения делимости 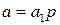 ,
, 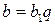 , где
, где  и
и  – целые числа. Тогда
– целые числа. Тогда
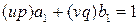 , а, значит, числа
, а, значит, числа 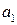 и
и  взаимно просты.
взаимно просты.
Следствие 2. Рассмотрим целые числа  ,
,  и
и  . Если
. Если 

 и
и 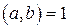 , то
, то 

 .
.
Доказательство. По теореме условие 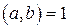 можно записать в
можно записать в
следующем виде: 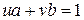 , где
, где 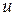 и
и 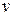 – целые числа. По определению делимости условие
– целые числа. По определению делимости условие 

 означает, что найдется такое целое число
означает, что найдется такое целое число 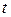 , что
, что 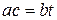 . Умножим обе части последнего равенства на
. Умножим обе части последнего равенства на 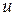 , получим
, получим 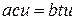 . Но
. Но  , тогда
, тогда
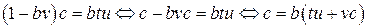 .
.
Поскольку 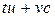 – целое число, последнее равенство означает, что
– целое число, последнее равенство означает, что 

 .
.
Дата добавления: 2021-03-18; просмотров: 174; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
