Операции над красно-черными деревьями
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Тюменский государственный нефтегазовый университет»
Институт менеджмента и бизнеса
Кафедра Математические методы в экономике
КУРСОВАЯ РАБОТА
По курсу Основы алгоритмизации и языки программирования
На тему Красно-черные деревья
Выполнил: ст. гр. ММЭ-09-1
Кондрашева Мария
Руководитель: ст. преподаватель
Наурусова Г. А.
Тюмень,2011
Содержание
Введение. 3
1. Структуры данных: деревья.. 5
1.1 Структуры данных. 5
1.2 Деревья. 6
1.3 Бинарные деревья. 11
1.4 Бинарные деревья поиска. 11
1.5 Красно-черные деревья. 13
1.6 Операции над красно-черными деревьями. 16
1.6.1 Повороты.. 16
1.6.2 Вставка. 17
1.6.3 Удаление. 25
1.6.4 Поиск узла с заданным ключом. 31
1.6.5 Поиск минимума и максимума. 32
2. Автоматизация операций над красно-чёрными деревьями 34
заключение. 46
список литературы: 47
Приложение 1. Листинг программы.. 48
|
|
|
Введение
Множество — это фундаментальное понятие, как в математике, так и в теории вычислительных машин. Тогда как математические множества остаются неизменными, множества, которые обрабатываются в ходе выполнения алгоритмов, могут с течением времени разрастаться, уменьшаться, или подвергаться другим изменениям. Назовем такие множества динамическими (dynamic). В данной работе описывается метод представления конечных динамических множеств в виде красно-чёрных деревьев – один из основных методов представления конечных динамических множеств.
Объектом данной работы является разновидность структур данных красно-чёрные деревья.
Красно-черные деревья это вариант классических двоичных деревьев, использующий эффективный механизм поддержания сбалансированности дерева.
В качестве предмета данной работы выступают операции, выполняемые над красно-чёрными деревьями.
Целью данной работы является изучение красно-чёрных деревьев и исследование их основных свойств, а также автоматизация операций для работы с ними на Turbo Pascal 7.0. Для этого необходимо выполнить следующие задачи:
· исследовать основные понятия красно-чёрных деревьев;
|
|
|
· изучить основные операции, выполняемые над красно-чёрными деревьями;
· автоматизировать основные операции, выполняемые над красно-чёрными деревьями, в общем виде на языке Turbo Pascal;
· сделать выводы по выполненной работе.
Красно-чёрные деревья являются одними из наиболее активно используемых на практике самобалансирующихся деревьев поиска. В частности, контейнер map в большинстве реализаций библиотеки STL языка C++, класс TreeMap языка Java, так же, как и многие другие реализации ассоциативного массива в различных библиотеках, основаны на красно-чёрных деревьях.
Популярность красно-чёрных деревьев связана с тем, что на них часто достигается подходящий баланс между степенью сбалансированности и сложностью поддержки сбалансированности.
Структуры данных: деревья
Структуры данных
Структура данных - совокупность физически (типы данных) и логически (алгоритм, функции) взаимосвязанных переменных и их значений.
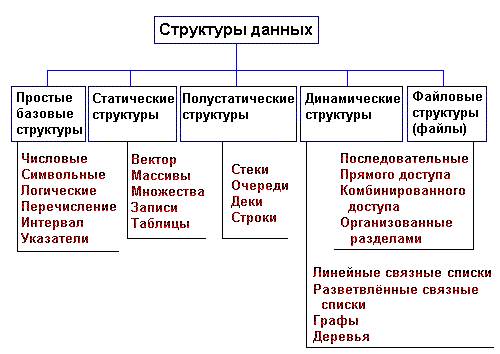
Рис. 1. Классификация структур данных.
Различаются ПРОСТЫЕ (базовые, примитивные) структуры (типы) данных и ИНТЕГРИРОВАННЫЕ (структурированные, композитные, сложные). Простыми называются такие структуры данных, которые не могут быть расчленены на составные части, большие, чем биты. Интегрированными называются такие структуры данных, составными частями которых являются другие структуры данных - простые или в свою очередь интегрированные. Интегрированные структуры данных конструируются программистом с использованием средств интеграции данных, предоставляемых языками программирования.
|
|
|
В зависимости от отсутствия или наличия явно заданных связей между элементами данных следует различать НЕСВЯЗНЫЕ структуры (векторы, массивы, строки, стеки, очереди) и СВЯЗНЫЕ структуры (связные списки).
Весьма важный признак структуры данных - ее изменчивость - изменение числа элементов и (или) связей между элементами структуры. В определении изменчивости структуры не отражен факт изменения значений элементов данных, поскольку в этом случае все структуры данных имели бы свойство изменчивости. По признаку изменчивости различают структуры СТАТИЧЕСКИЕ, ПОЛУСТАТИЧЕСКИЕ, ДИНАМИЧЕСКИЕ. Классификация структур данных по признаку изменчивости приведена на рис. 1. Базовые структуры данных, статические, полустатические и динамические характерны для оперативной памяти и часто называются оперативными структурами. Файловые структуры соответствуют структурам данных для внешней памяти.
|
|
|
Важный признак структуры данных - характер упорядоченности ее элементов. По этому признаку структуры можно делить на ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ структуры.
В зависимости от характера взаимного расположения элементов в памяти линейные структуры можно разделить на структуры с ПОСЛЕДОВАТЕЛЬНЫМ распределением элементов в памяти (векторы, строки, массивы, стеки, очереди) и структуры с ПРОИЗВОЛЬНЫМ СВЯЗНЫМ распределением элементов в памяти (односвязные, двусвязные списки). Пример нелинейных структур - многосвязные списки, деревья, графы.
В языках программирования понятие "структуры данных" тесно связано с понятием "типы данных". Любые данные, т.е. константы, переменные, значения функций или выражения, характеризуются своими типами.
Информация по каждому типу однозначно определяет :
1) структуру хранения данных указанного типа, т.е. выделение памяти и представление данных в ней, с одной стороны, и интерпретирование двоичного представления, с другой;
2) множество допустимых значений, которые может иметь тот или иной объект описываемого типа;
3) множество допустимых операций, которые применимы к объекту описываемого типа.
Деревья
Деревья – наиболее важные нелинейные структуры, которые встречаются при работе с компьютерными алгоритмами. Вообще говоря, древовидная структура задает для узлов отношение «ветвления», которое во многом напоминает строение обычного дерева [2].
Формально дерево (tree) определяется как конечное множество Т одного или более узлов со следующими свойствами:
А) существует один выделенный узел, а именно – корень (root) данного дерева Т;
Б) остальные узлы (за исключением корня) распределены среди  непересекающихся множеств
непересекающихся множеств  и каждое из этих множеств, в свою очередь, является деревом; деревья
и каждое из этих множеств, в свою очередь, является деревом; деревья  называются поддеревьями (subtrees) данного корня.
называются поддеревьями (subtrees) данного корня.
Из этого определения следует, что каждый узел дерева является корнем некоторого поддерева данного дерева. Количество поддеревьев узла называется степенью (degree) этого узла. Узел со степенью нуль называется концевым узлом (terminal node) или листом (leaf). Неконцевой узел называется узлом ветвления (branch node). Уровень (level) узла по отношению к дереву Т определяется рекурсивно следующим образом. Уровень корня дерева Т равен нулю, а уровень любого другого узла на единицу выше, чем уровень корня ближайшего поддерева дерева Т, содержащего данный узел.
Эти понятия иллюстрируются на рис. 2 на примере дерева с семью узлами. Узел А является корнем, который имеет два поддерева: 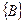 и
и  . Корнем дерева
. Корнем дерева  является узел С. Уровень узла С равен 1 по отношению ко всему дереву. Он имеет три поддерева,
является узел С. Уровень узла С равен 1 по отношению ко всему дереву. Он имеет три поддерева, 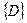 ,
,  и
и  , поэтому С имеет степень 3. Концевыми на рис. 2 являются узлы
, поэтому С имеет степень 3. Концевыми на рис. 2 являются узлы 
 и
и 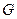 . Узел
. Узел  - единственный узел со степенью 1, а узел
- единственный узел со степенью 1, а узел 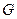 - единственный узел со степенью 3.
- единственный узел со степенью 3.
Если в п. Б данного выше определения имеет значение относительный порядок поддеревьев  , то дерево является упорядоченным (ordered tree). Если в упорядоченном дереве
, то дерево является упорядоченным (ordered tree). Если в упорядоченном дереве 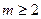 , то имеет смысл назвать поддерево
, то имеет смысл назвать поддерево 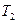 вторым поддеревом данного корня и т.д. Упорядоченные деревья иногда также называются плоскими деревьями (plane trees), поскольку при их упорядочении имеет значение способ размещения дерева на плоскости. Если не считать различными два дерева, которые отличаются только относительным порядком поддеревьев узлов, то дерево называется ориентированным (oriented), поскольку при этом имеет значение только относительная ориентация узлов, а не их порядок. Сама природа представления данных в компьютере определяет неявный порядок любого дерева, поэтому в большинстве случаев упорядоченные деревья представляют наибольший интерес. Далее будем неявно предполагать, что все рассматриваемые деревья являются упорядоченными, если явно не указано обратное. Соответственно деревья на рис. 2 и 3 в общем случае рассматриваются как разные, хотя как ориентированные деревья они совершенно одинаковые.
вторым поддеревом данного корня и т.д. Упорядоченные деревья иногда также называются плоскими деревьями (plane trees), поскольку при их упорядочении имеет значение способ размещения дерева на плоскости. Если не считать различными два дерева, которые отличаются только относительным порядком поддеревьев узлов, то дерево называется ориентированным (oriented), поскольку при этом имеет значение только относительная ориентация узлов, а не их порядок. Сама природа представления данных в компьютере определяет неявный порядок любого дерева, поэтому в большинстве случаев упорядоченные деревья представляют наибольший интерес. Далее будем неявно предполагать, что все рассматриваемые деревья являются упорядоченными, если явно не указано обратное. Соответственно деревья на рис. 2 и 3 в общем случае рассматриваются как разные, хотя как ориентированные деревья они совершенно одинаковые.
 Рис. 2. Пример дерева. Рис. 3. Пример дерева.
Рис. 2. Пример дерева. Рис. 3. Пример дерева.
Лес (forest) – это множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев. Тогда еще одна формулировка п. (Б) в данном выше определении дерева могла бы выглядеть так: узлы дерева при условии исключения корня образуют лес.
При удалении корня дерева получим лес, и наоборот: при добавлении нового узла, получим дерево. Поэтому понятия «лес» и «дерево» часто используются как равнозначные при работе со структурами данных.
Графически деревья можно представить по-разному. Например, для дерева на рис.2. существует еще три принципиально отличных альтернативных варианта, которые, как показано на рис. 4., отличаются расположением узлов относительно корня. Но изучение литературы и многочисленные неформальные обсуждения широкого круга алгоритмов со специалистами в области информатики показали, что в более чем 80% рассмотренных случаев деревья изображаются с корнем вверху. Поэтому схема дерева будет выглядеть так, как на рис. 4., (b), т.е. с корнем вверху и листьями внизу. В соответствии с такой ориентацией назовём корневой узел вершиной (apex) дерева и будем характеризовать уровни узлов как мелкие и глубокие.

Рис. 4. Как следует рисовать деревья?
Для рассмотрения деревьев необходимо создать хорошую описательную терминологию. На рис. 18 показаны два наиболее распространенных типа генеалогических деревьев. Они отличаются тем, что в родословной показаны предки конкретного человека, а в родовой схеме – его наследники [2].
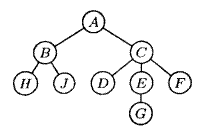
Рис. 5. Обычная схема дерева.
Стандартная терминология древовидных структур происходит от генеалогических деревьев второго типа, а именно – от родовой схемы. Каждый узел называется родителем (parent) корней его поддеревьев, а сами корни называются братьями-сестрами (siblings), а также детьми (children) своего родителя. Корень всего дерева не имеет родителя. Например, на рис. 5 узел C имеет трех детей, D, E и F, узел E является родителем узла G, а узлы B и C являются братьями-сестрами. Узел имеет не более одного родителя или предка.

Бинарные деревья
Родословная, показанная на рис. 18,(а), является примером бинарного дерева (binary tree) – одного из наиболее важных типов деревьев. Каждый узел бинарного дерева имеет не более двух поддеревьев, причем в случае только одного поддерева следует различать левое и правое. Строго говоря, бинарное дерево – это конечное множество узлов, которое является пустым или состоит из корня и двух непересекающихся бинарных деревьев, которые называются левым и правым поддеревьями данного корня.
Обратите внимание на то, что бинарное дерево не является особым типом ранее определенного обычного дерева. На самом деле это совершенно другое понятие. Например, бинарные деревья

являются различными, так как в первом случае корень имеет пустое правое поддерево, а в другом – пустое левое поддерево. Однако как деревья они совершенно идентичны. Бинарное дерево может быть пустым, а обычное – нет. Следовательно, при работе бинарными деревьями нужно не забывать об обязательном эпитете «бинарный», чтобы не путать их с обычными деревьями [2].
Бинарные деревья поиска
Как следует из названия, бинарное дерево поиска в первую очередь является бинарным деревом, как показано на рис. 6. Такое дерево может быть представлено при помощи связанной структуры данных, в которой каждый узел является объектом. В дополнение к полям ключа key и сопутствующих данных, каждый узел содержит поля left, right и р, которые указывают на левый и правый дочерние узлы и на родительский узел соответственно. Если дочерний или родительский узел отсутствуют, соответствующее поле содержит значение NIL. Единственный узел, указатель р которого равен nil, - это корневой узел дерева. Ключи в бинарном дереве поиска хранятся таким образом, чтобы в любой момент удовлетворять следующему свойству бинарного дерева поиска.
Если х - узел бинарного дерева поиска, а узел у находится в левом поддереве x, то 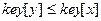 . Если узел у находится в правом поддереве х, то
. Если узел у находится в правом поддереве х, то  .
.
Так, на рис. 6а ключ корня равен 5, ключи 2, 3 и 5, которые не превышают значение ключа в корне, находятся в его левом поддереве, а ключи 7 и 8, которые не меньше, чем ключ 5, - в его правом поддереве. То же свойство, как легко убедиться, выполняется для каждого другого узла дерева. На рис. 6б показано дерево с теми же узлами и обладающее тем же свойством, однако менее эффективное в работе, поскольку его высота равна 4, в отличие от дерева на рис. 6а, высота которого равна 2.

Рис. 6. Бинарные деревья поиска
Свойство бинарного дерева поиска позволяет нам вывести все ключи, находящиеся в дереве, в отсортированном порядке с помощью простого рекурсивного алгоритма, называемого центрированным (симметричным) обходом дерева (inorder tree walk). Этот алгоритм получил данное название в связи с тем, что ключ в корне поддерева выводится между значениями ключей левого поддерева и правого поддерева. Имеются и другие способы обхода, а именно - обход в прямом порядке (preorder tree walk), при котором сначала выводится корень, а потом - значения левого и правого поддерева, и обход в обратном порядке (postorder tree walk), когда первыми выводятся значения левого и правого поддерева, а уже затем - корня. Центрированный обход дерева Т реализуется процедурой  :
:
Inorder_Tree_Walk(x)
1 if 
2 then Inorder_Tree_Walk(left[x])
3 print key [ x ]
4 Inorder_Tree_Walk( right [x])
В качестве примера рассмотрите центрированный обход деревьев, показанных на рис. 6, - вы получите в обоих случаях один и тот же порядок ключей, а именно 2, 3, 5, 5, 7, 8. Корректность описанного алгоритма следует непосредственно из свойства бинарного дерева поиска.
Для обхода дерева требуется время O(n), поскольку после начального вызова процедура вызывается ровно два раза для каждого узла дерева: один раз для его левого дочернего узла, и один раз - для правого [3].
Красно-черные деревья
Красно-чёрное дерево (red-black tree) – это двоичное дерево поиска, вершины которого разделены на красные (red) и чёрные (black). Таким образом, каждая вершина хранит один дополнительный бит – её цвет [3].
При этом должны выполняться определённые требования, которые гарантируют, что глубины любых двух листьев отличаются не более чем в два раза, поэтому дерево можно назвать сбалансированным (balanced).
Каждая вершина красно-чёрного дерева имеет поля color (цвет), key (ключ), left (левый ребёнок), right (правый ребёнок) и p (родитель). Если у вершины отсутствует ребёнок или родитель, соответствующее поле содержит NIL. Для удобства будем считать, что значения NIL, хранящиеся в полях left и right, являются ссылками на дополнительные (фиктивные) листья дерева. В таком пополненном дереве каждая старая вершина (содержащая ключ) имеет двух детей [3].
Двоичное дерево поиска называется красно-чёрным деревом, если оно обладает следующими свойствами (будем называть их RB -свойствами, по-английски red-black properties):
1. Каждая вершина – либо красная, либо чёрная.
2. Каждый лист (NIL) – чёрный.
3. Если вершина красная, оба её ребёнка чёрные.
4. Все пути, идущие вниз от корня к листьям, содержат одинаковое количество чёрных вершин [1].
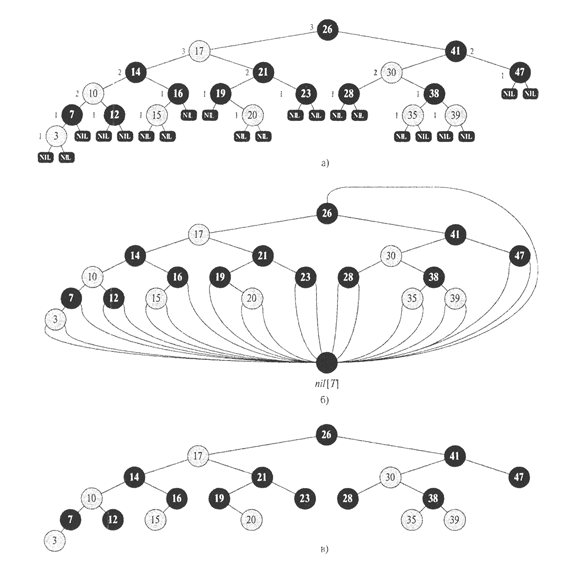
Рис. 7. Красно-чёрное дерево. Чёрные вершины показаны как тёмные, красные – как серые. Каждая вершина либо красная, либо чёрная. Все NIL-листья чёрные. Дети красной вершины – чёрные. Для каждой вершины все пути от неё вниз к листьям содержат одинаковое количество чёрных вершин. Около каждой вершины (кроме листьев) записана её чёрная высота. Чёрная высота листьев равна 0.
Рассмотрим произвольную вершину x красно-чёрного дерева и пути, ведущие вниз от неё к листьям. Все они содержат одно и то же число чёрных вершин (добавим к ним путь из корня в x и применим свойство 4). Число чёрных вершин в любом из них (саму вершину x не считаем) будем называть чёрной высотой (black-height) вершины x и обозначать bh(x). Чёрной высотой дерева будем считать чёрную высоту его корня.
Следующая лемма показывает, что красно-чёрные деревья хороши как деревья поиска.
Лемма. Красно-чёрное дерево с n внутренними вершинами (т.е. не считая NIL -листьев) имеет высоту не больше 2 lg ( n +1).
Доказательство. Сначала покажем, что поддерево с корнем в x содержит по меньшей мере 2bh(x)-1 внутренних вершин. Доказательство проведём индукцией от листьев к корню. Для листьев чёрная высота равна 0, и поддерево в самом деле содержит не менее 2bh(x)-1=20-1=0 внутренних вершин. Пусть теперь вершина x не является листом и имеет чёрную высоту k. Тогда оба её ребёнка имеют чёрную высоту не меньше k -1 (красный ребёнок будет иметь высоту k, чёрный - k -1). По предположению индукции левое и правое поддеревья вершины x содержат не менее 2k-1-1 вершин, и потому поддерево с корнем x содержит, по меньшей мере, 2k-1-1+2k-1-1+1=2k-1 внутренних вершин.
Чтобы завершить доказательство леммы, обозначим высоту дерева через h. Согласно свойству 3, по крайней мере, половина узлов на пути от корня к листу, не считая сам корень, должны быть черными. Следовательно, черная высота корня должна составлять как минимум h /2; следовательно,
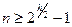
Перенося 1 в левую часть и логарифмируя, получим, что 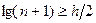 , или
, или  .
.
Непосредственным следствием леммы является то, что такие операции над динамическими множествами, как Search, Minimum, Maximum, Predecessor и SUCCESSOR, при использовании красно-черных деревьев выполняются за время О(lg(h)), поскольку время работы этих операций на дереве поиска высотой h составляет О(h), а любое красно-черное дерево с n узлами является деревом поиска высотой О (lg(n)). Хотя алгоритмы Tree_Insert и Tree_Delete характеризуются временем работы О(lg(n)), если использовать их для вставки и удаления из красно-черного дерева, непосредственно использовать их для выполнения операций Insert и Delete нельзя, поскольку они не гарантируют сохранение красно-черных свойств после внесения изменений в дерево [3].
Операции над красно-черными деревьями
Повороты
Операции над деревом поиска Tree_Insert и Tree_Delete, будучи применены к красно-черному дереву с n ключами, выполняются за время O(lg(n)). Поскольку они изменяют дерево, в результате их работы могут нарушаться красно-черные свойства. Для восстановления этих свойств мы должны изменить цвета некоторых узлов дерева, а также структуру его указателей.

Рис. 8. Операции поворота в бинарном дереве поиска.
Изменения в структуре указателей будут выполняться при помощи поворотов (rotations), которые представляют собой локальные операции в дереве поиска, сохраняющие свойство бинарного дерева поиска. На рис. 6 показаны два типа поворотов - левый и правый (здесь  ,
, 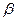 и
и 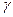 - произвольные поддеревья). При выполнении левого поворота в узле x предполагается, что его правый дочерний узел y не является листом nil[T]. Левый поворот выполняется "вокруг" связи между x и y, делая y новым корнем поддерева, левым дочерним узлом которого становится x, а бывший левый потомок узла y - правым потомком x.
- произвольные поддеревья). При выполнении левого поворота в узле x предполагается, что его правый дочерний узел y не является листом nil[T]. Левый поворот выполняется "вокруг" связи между x и y, делая y новым корнем поддерева, левым дочерним узлом которого становится x, а бывший левый потомок узла y - правым потомком x.
В псевдокоде процедуры LEFT_ROTATE предполагается, что  , а родитель корневого узла - nil [Т].
, а родитель корневого узла - nil [Т].
Left_Rotate(T , x)
1  > Устанавливаем у.
> Устанавливаем у.
2 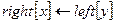 > Левое поддерево у становится
> Левое поддерево у становится
> правым поддеревом х
3 if 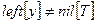
4 then 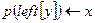
5 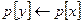 > Перенос родителя х в у
> Перенос родителя х в у
6 if 
7 then 
8 else if 
9 then 
10 else 
11 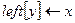 > x - левый дочерний y
> x - левый дочерний y
12 

Рис. 9. Пример выполнения процедуры LEFT_ROTATE.
Код процедуры Right_Rotate симметричен коду Left_Rotate. Обе эти процедуры выполняются за время O (1). При повороте изменяются только указатели, все остальные поля сохраняют свое значение [3].
Вставка
Вставка узла в красно-черное дерево с n узлами может быть выполнена за время О(lg(n)). Для того чтобы вставка сохраняла красно-черные свойства дерева, после нее вызывается вспомогательная процедура RB_INSERT_FIXUP, которая перекрашивает узлы и выполняет повороты. Вызов RB_Insert(T, z) вставляет в красно-черное дерево Т узел z с заполненным полем key:
RB Insert(T, z)
1 
2 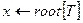
3 while 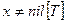
4 do 
5 if 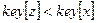
6 then 
7 else 
8 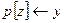
9 if 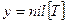
10 then 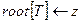
11 else if 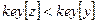
12 then 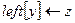
13 else 
14 
15 
16 
17 RB_INSERT_FIXUP(T, z)
Поскольку красный цвет z может вызвать нарушение одного из красно-черных свойств, в строке 17 вызывается вспомогательная процедура RB_Insert_Fixup(T, z), предназначение которой - восстановить красно-черные свойства дерева:
RB_Insert_Fixup(T, z)
1 while 
2 do if 
3 then 
4 if 
5 then 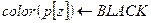 > Случай 1
> Случай 1
6 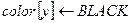 > Случай 1
> Случай 1
7  > Случай 1
> Случай 1
8  > Случай 1
> Случай 1
9 else if 
10 then z 4- p[z] > Случай 2
11 Left_Rotate(T, z) > Случай 2
12  > Случай 3
> Случай 3
13 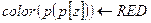 > Случай 3
> Случай 3
14  > Случай 3
> Случай 3
15 else (то же, что и в " then ", с заменой left на right и наоборот)
16 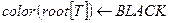
Для того чтобы понять, как работает процедура RB_INSERT_FIXUP, разобьем рассмотрение кода на три основные части. Сначала определим, какие из красно-черных свойств нарушаются при вставке узла z и окраске его в красный цвет. Затем рассмотрим предназначение цикла while в строках 1-15. После этого изучим каждый из трех случаев, которые встречаются в этом цикле, и посмотрим, каким образом достигается цель в каждом случае. На рис. 8 показан пример выполнения процедуры RB_INSERT_FIXUP.
Какие из красно-черных свойств могут быть нарушены перед вызовом RB_InSERT_Fixup? Свойство 1 определенно выполняется (как и свойство 3), так как оба дочерних узла вставляемого узла являются ограничителями nil [ T ]. Свойство 5, согласно которому для каждого узла все пути от него до листьев, являющихся потомками данного узла, содержат одно и то же количество черных узлов, также остается в силе, поскольку узел z замещает (черный) ограничитель, будучи при этом красным и имея черные дочерние узлы. Таким образом, может нарушаться только свойство 2, которое требует, чтобы корень красно-черного дерева был черным, и свойство 4, согласно которому красный узел не может иметь красного потомка. Оба нарушения возможны в силу того, что узел z после вставки окрашивается в красный цвет. Свойство 2 оказывается нарушенным, если узел z становится корнем, а свойство 4 - если родительский по отношению к z узел является красным. На рис. 8а показано нарушение свойства 4 после вставки узла z.
Цикл while в строках 1-15 сохраняет следующий инвариант, состоящий из трех частей.
В начале каждой итерации цикла:
а) узел z красный;
б) если р[ z ] - корень дерева, то р[ z ] — черный узел;
в) если имеется нарушение красно-черных свойств, то это нарушение только одно - либо нарушение свойства 2, либо свойства 4. Если нарушено свойство 2, то это вызвано тем, что корнем дерева является красный узел z; если нарушено свойство 4, то в этом случае красными являются узлы z и p [ z ].
Часть в, в которой говорится о возможных нарушениях красно-черных свойств, наиболее важна для того, чтобы показать, что процедура RB_Insert_Fixup восстанавливает красно-черные свойства. Части а и б просто поясняют ситуацию.
Поскольку мы сосредотачиваем свое рассмотрение только на узле z и узлах, находящихся в дереве вблизи него, полезно знать, что узел z - красный (часть а). Часть б используется для того, чтобы показать, что узел  к которому мы обращаемся в строках 2, 3, 7, 8, 13 и 14, существует.
к которому мы обращаемся в строках 2, 3, 7, 8, 13 и 14, существует.
Инициализация. Перед выполнением первой итерации цикла имеется красно-черное дерево без каких-либо нарушений красно-черных свойств, к которому мы добавляем красный узел z. Покажем, что все части инварианта цикла выполняются к моменту вызова процедуры RB_Insert_Fixup.
а) В момент вызова процедуры RB_Insert_Fixup узел z — вставленный в дерево красный узел.
б) Если р[z] - корневой узел дерева, то он является черным и не изменяется до вызова процедуры RB_lNSERT_Fixup.
в) Мы уже убедились в том, что красно-черные свойства 1, 3 и 5 сохраняются к моменту вызова процедуры RB_Insert_Fixup.
Если нарушается свойство 2, то красный корень должен быть добавленным в дерево узлом z, который при этом является единственным внутренним узлом дерева. Поскольку и родитель, и оба потомка z являются ограничителями, свойство 4 не нарушается. Таким образом, нарушение свойства 2 - единственное нарушение красно-черных свойств во всем дереве.
Если же нарушено свойство 4, то поскольку дочерние по отношению к z узлы являются черными ограничителями, а до вставки z никаких нарушений красно-черных свойств в дереве не было, нарушение заключается в том, что и z, и р[z] - красные. Кроме этого, других нарушений красно-черных свойств не имеется.
Завершение. Как видно из кода, цикл завершает свою работу, когда р[z] становится черным (если z - корневой узел, то р[z] представляет собой черный ограничитель nil[Т]). Таким образом, свойство 4 при завершении цикла не нарушается. В соответствии с инвариантом цикла, единственным нарушением красно-черных свойств может быть нарушение свойства 2. В строке 16 это свойство восстанавливается, так что по завершении работы процедуры RB_Insert_Fixup все красно-черные свойства дерева выполняются.
Сохранение. При работе цикла while следует рассмотреть шесть разных случаев, однако три из них симметричны другим трем; разница лишь в том, является ли родитель р[z] левым или правым дочерним узлом по отношению к своему родителю р[р[z]], что и выясняется в строке 2 (мы привели код только для ситуации, когда р[z] является левым потомком). Узел р[р[z]] существует, поскольку, в соответствии с частью б) инварианта цикла, если р[z] - корень дерева, то он черный. Поскольку цикл начинает работу, только если р[z] - красный, то р[z] не может быть корнем. Следовательно, р[р[z]] существует. Случай 1 отличается от случаев 2 и 3 цветом "брата" родительского по отношению к z узла, т.е. "дяди" узла z. После выполнения строки 3 указатель у указывает на дядю узла z - узел right[р[р[z]]], и в строке 4 выясняется его цвет. Если у - красный, выполняется код для случая 1; в противном случае выполняется код для случаев 2 и 3. В любом случае, узел р[р[z]] - черный, поскольку узел р[z] - красный, а свойство 4 нарушается только между z np[z].

Рис. 10. Работа процедуры RB_INSERT_FIXUP
Случай 1: узел у красный.
На рис. 11 показана ситуация, возникающая в случае 1 (строки 5-8), когда и p[z], и у - красные узлы. Поскольку p[p[z]] - черный, мы можем исправить ситуацию, покрасив и p[z], и у в черный цвет (после чего цвет красного родителя узла z становится черным, и нарушение между z и его родителем исчезает), а р[р[z]] - в красный цвет, для того чтобы выполнялось свойство 5. После этого мы повторяем цикл while с узлом р[р[z]] в качестве нового узла z. Указатель z перемещается, таким образом, на два уровня вверх.
На рис. 11а z - правый дочерний узел, а на рис. 11б - левый. Как видите, предпринимаемые в обоих случаях одни и те же действия приводят к одинаковому результату. Все поддеревья (  и
и 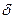 ) имеют черные корни и одинаковое значение черной высоты. После перекраски свойство 5 сохраняется: все нисходящие пути от узла к листьям содержат одинаковое число черных узлов. После выполнения итерации новым узлом z становится узел р[р[z]] и нарушение свойства 4 может быть только между новым узлом z и его родителем (который также может оказаться красным).
) имеют черные корни и одинаковое значение черной высоты. После перекраски свойство 5 сохраняется: все нисходящие пути от узла к листьям содержат одинаковое число черных узлов. После выполнения итерации новым узлом z становится узел р[р[z]] и нарушение свойства 4 может быть только между новым узлом z и его родителем (который также может оказаться красным).
Теперь покажем, что в случае 1 инвариант цикла сохраняется. Обозначим через z узел z в текущей итерации, а через z'=р[р[z]] - узел z, проверяемый в строке 1 при следующей итерации.
а) Поскольку в данной итерации цвет узла р[р[z]] становится красным, в начале следующей итерации узел z' - красный.
б) Узел р[z'] в текущей итерации - р[р[р[z]]], и цвет данного узла в пределах данной итерации не изменяется. Если это корневой узел, то его цвет до начала данной итерации был черным и остается таковым в начале следующей итерации.
в) Мы уже доказали, что в случае 1 свойство 5 сохраняется; кроме того, понятно, что при выполнении итерации не возникает нарушение свойств 1 или 3.
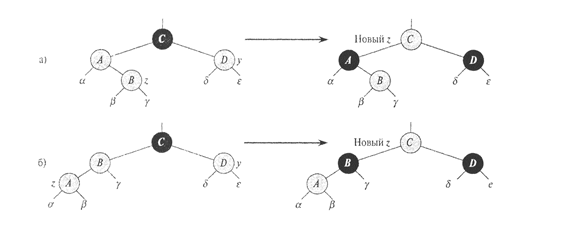
Рис. 11. Случай 1 процедуры RB_lNSERT_FlXUP
Если узел z' в начале очередной итерации является корнем, то код, соответствующий случаю 1, корректирует единственное нарушение свойства 4. Поскольку узел z' - красный и корневой, единственным нарушенным становится свойство 2, причем это нарушение связано с узлом z'.
Если узел z' в начале следующей итерации корнем не является, то код, соответствующий случаю 1, не вызывает нарушения свойства 2. Этот код корректирует единственное нарушение свойства 4, имеющееся перед выполнением итерации. Коррекция выражается в том, что узел z' становится красным, в то время как цвет узла р[z'] не изменяется. Если узел р[z'] был черным, то свойство 4 не нарушается; если же этот узел был красным, то окрашивание узла z' в красный цвет приводит к нарушению свойства 4 между узлами z' и р[z'].
Случай 2: узел у черный и z — правый потомок.
Случай 3: узел у черный и z — левый потомок.
В случаях 2 и 3 цвет узла у, являющегося "дядей" узла z, черный. Эти два случая отличаются друг от друга тем, что z является левым или правым дочерним узлом по отношению к родительскому. Строки 10-11 псевдокода соответствуют случаю 2, который показан на рис. 12 вместе со случаем 3. В случае 2 узел z является правым потомком своего родительского узла. Используем левый поворот для преобразования сложившейся ситуации в случай 3 (строки 12-14), когда z является левым потомком. Поскольку и z, и р[z] - красные узлы, поворот не влияет ни на черную высоту узлов, ни на выполнение свойства 5. Когда мы приходим к случаю 3 (либо непосредственно, либо поворотом из случая 2), узел у имеет черный цвет (поскольку иначе мы бы получили случай 1). Кроме того, обязательно существует узел р[р[ z ]], так как мы доказали, что этот узел существовал при выполнение строк 2 и 3, а также что после перемещения узла z на один узел вверх в строке 10 с последующим опусканием в строке 11 узел р[р[ z ]] остается неизменным. В случае 3 мы выполняем ряд изменений цвета и правых поворотов, которые сохраняют свойство 5. После этого, так как у нас нет двух идущих подряд красных узлов, работа процедуры завершается. Больше тело цикла while не выполняется, так как узел р[ z ] теперь черный.
Теперь покажем, что случаи 2 и 3 сохраняют инвариант цикла.
а) В случае 2 выполняется присвоение, после которого z указывает на красный узел р[ z ]. Никаких других изменений z или его цвета в случаях 2 и 3 не выполняется.
б) В случае 3 узел р[ z ] делается черным, так что если р[ z ] в начале следующей итерации является корнем, то этот корень - черный.
в) Как и в случае 1, в случае 2 и 3 свойства 1, 3 и 5 сохраняются. Поскольку узел z в случаях 2 и 3 не является корнем, нарушение свойства 2 невозможно. Случаи 2 и 3 не могут приводить к нарушению свойства 2, поскольку при повороте в случае 3 красный узел становится дочерним по отношению к черному.
Таким образом, случаи 2 и 3 приводят к коррекции нарушения свойства 4, при этом не внося никаких новых нарушений красно-черных свойств.
Показав, что при любой итерации инвариант цикла сохраняется, мы тем самым показали, что процедура RB_Insert_Fixup корректно восстанавливает красно-черные свойства дерева [3].

Рис. 12. Случаи 2 и 3 процедуры RB_Insert_Fixup
Удаление
RB_Delete(T, z)
1 if left[z]=nil[T] или right[z]=nil[T]
2 then 
3 else 
4 if 
5 then 
6 else 
7 
8 if p[y] = nil[T]
9 then 
10 else if 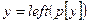
11 then 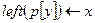
12 else 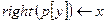
13 if 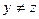
14 then 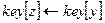
15 Копируем сопутствующие данные у в z
16 if color[у]=BLACK
17 then RB_Delete_Fixup(T, x)
18 return у
Если узел у - красный, красно-черные свойства при извлечении у из дерева сохраняются в силу следующих причин:
• никакая черная высота в дереве не изменяется;
• никакие красные узлы не становятся соседними;
• так как у не может быть корнем в силу своего цвета, корень остается черным.
Узел х, который передается в качестве параметра во вспомогательную процедуру RB_Delete_Fixup, является одним из двух узлов: либо это узел, который был единственным потомком у перед извлечением последнего из дерева (если у у был дочерний узел, не являющийся ограничителем), либо, если у узла у нет дочерних узлов, х является ограничителем nil [ T ]. В последнем случае безусловное присвоение в строке 7 гарантирует, что родительским по отношению к х узлом становится узел, который ранее был родителем у, независимо от того, является ли х внутренним узлом с реальным ключом или ограничителем nil [ T ].
RB_DELETE_Fixup(T, х)
1 while 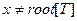 и color[x]=BLACK
и color[x]=BLACK
2 do if 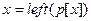
3 then 
4 if 
5 then  > Случай 1
> Случай 1
6  > Случай 1
> Случай 1
7 Left_Rotate(T,p[z]) > Случай 1
8  > Случай 1
> Случай 1
9 if color[left[w]]=BLACK и color[right[w]]=BLACK
10 then  > Случай 2
> Случай 2
11 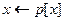 > Случай 2
> Случай 2
12 else if color[right[w]]=BLACK
13 then 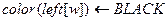 > Случай 3
> Случай 3
14  > Случай 3
> Случай 3
15 Right_Rotate(T, w) > Случай 3
16  > Случай 3
> Случай 3
17  > Случай 4
> Случай 4
18  > Случай 4
> Случай 4
19 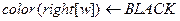 > Случай 4
> Случай 4
20 LEFT_ROTATE(r,p[x]) > Случай 4
21  > Случай 4
> Случай 4
22 else (то же, что и в " then ", с заменой left на right и наоборот)
23 
Если извлекаемый из дерева в процедуре RB_Delete узел у черный, то могут возникнуть три проблемы. Во-первых, если у был корнем, а теперь корнем стал красный потомок у, нарушается свойство 2. Во-вторых, если и х, и р[у] (который теперь является также р[х]) были красными, то нарушается свойство 4. И, в-третьих, удаление у приводит к тому, что все пути, проходившие через у, теперь имеют на один черный узел меньше. Таким образом, для всех предков у оказывается нарушенным свойство 5. Мы можем исправить ситуацию, утверждая, что узел х - "сверхчерный", т.е. при рассмотрении любого пути, проходящего через х, добавлять дополнительную 1 к количеству черных узлов. При такой интерпретации свойство 5 остается выполняющимся. При извлечении черного узла у мы передаем его "черноту" его потомку. Проблема заключается в том, что теперь узел х не является ни черным, ни красным, что нарушает свойство 1. Вместо этого узел х окрашен либо "дважды черным", либо "красно-черным" цветом, что дает при подсчете черных узлов на пути, содержащем х, вклад, равный, соответственно, 2 или 1. Атрибут color узла х при этом остается равен либо BLACK (если узел дважды черный), либо RED (если узел красно-черный). Другими словами, цвет узла не соответствует его атрибуту color.
Процедура RB_Delete_Fixup восстанавливает свойства 1, 2 и 4. Цель цикла while в строках 1-22 состоит в том, чтобы переместить дополнительную черноту вверх по дереву до тех пор, пока не выполнится одно из перечисленных условий [3].
1. х указывает на красно-черный узел - в этом случае мы просто делаем узел х "единожды черным" в строке 23.
2. х указывает на корень - в этом случае мы просто убираем излишнюю черноту.
3. Можно выполнить некоторые повороты и перекраску, после которых двойная чернота будет устранена.
Внутри цикла while x всегда указывает на дважды черную вершину, не являющуюся корнем. В строке 2 мы определяем, является ли х левым или правым дочерним узлом своего родителя р[х]. Далее приведен подробный код для ситуации, когда х - левый потомок. Для правого потомка код аналогичен и симметричен, и скрыт за описанием в строке 22. Указатель w указывает на второго потомка родителя х. Поскольку узел х дважды черный, узел w не может быть nil[ T ] - в противном случае количество черных узлов на пути от р[х] к (единожды черному) листу было бы меньше, чем количество черных узлов на пути от р[х] к х.
Четыре разных возможных случая показаны на рис. 13. Перед тем как приступить к детальному рассмотрению каждого случая, убедимся, что в каждом из случаев преобразования сохраняется свойство 5. Ключевая идея заключается в необходимости убедиться, что при преобразованиях в каждом случае количество черных узлов (включая дополнительную черноту в х) на пути от корня включительно до каждого из поддеревьев  остается неизменным. Таким образом, если свойство 5 выполнялось до преобразования, то оно выполняется и после него. Например, на рис. 13а, который иллюстрирует случай 1, количество черных узлов на пути от корня до поддеревьев
остается неизменным. Таким образом, если свойство 5 выполнялось до преобразования, то оно выполняется и после него. Например, на рис. 13а, который иллюстрирует случай 1, количество черных узлов на пути от корня до поддеревьев  и
и 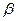 равно 3, как до, так и после преобразования (не забудьте о том, что узел х — дважды черный). Аналогично, количество черных узлов на пути от корня до любого из поддеревьев
равно 3, как до, так и после преобразования (не забудьте о том, что узел х — дважды черный). Аналогично, количество черных узлов на пути от корня до любого из поддеревьев 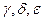 и
и  равно 2, как до, так и после преобразования. На рис. 13б подсчет должен включать значение с, равное значению атрибута color корня показанного поддерева, которое может быть либо red, либо BLACK. Так, на пути от корня до поддерева
равно 2, как до, так и после преобразования. На рис. 13б подсчет должен включать значение с, равное значению атрибута color корня показанного поддерева, которое может быть либо red, либо BLACK. Так, на пути от корня до поддерева  количество черных узлов равно 2 плюс величина, равная 1, если с равно black, и 0, если с равно red; эта величина одинакова до и после выполнения преобразований. В такой ситуации после преобразования новый узел х имеет атрибут color, равный с, но реально это либо красно-черный узел (если с = RED), либо дважды черный (если с = BLACK). Прочие случаи могут быть проверены аналогичным способом.
количество черных узлов равно 2 плюс величина, равная 1, если с равно black, и 0, если с равно red; эта величина одинакова до и после выполнения преобразований. В такой ситуации после преобразования новый узел х имеет атрибут color, равный с, но реально это либо красно-черный узел (если с = RED), либо дважды черный (если с = BLACK). Прочие случаи могут быть проверены аналогичным способом.
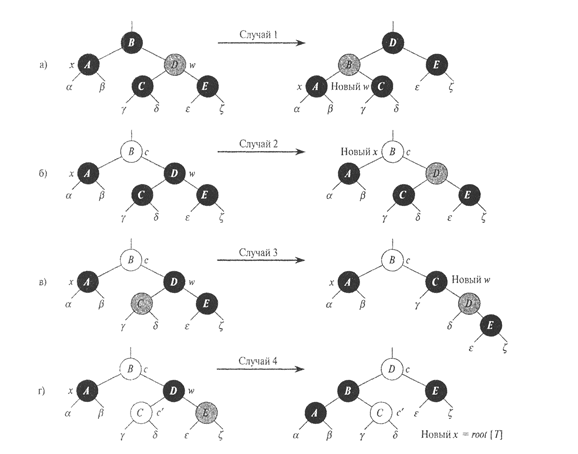
Рис. 13. Возможные ситуации, возникающие в цикле while процедуры RB_DeleteFixup. Темные узлы имеют цвет BLACK, темно-серые - RED, а светлые могут иметь любой цвет (на рисунке показан как с и с'). Греческими буквами показаны произвольные поддеревья
Случай 1: узел w красный.
Случай 1 (строки 5-8 процедуры RB_Delete_Fixup и рис. 13а) возникает, когда узел w ("брат" узла х) - красный. Поскольку w должен иметь черных потомков, можно обменять цвета w и р[х], а затем выполнить левый поворот вокруг р[х] без нарушения каких-либо красно-черных свойств. Новый "брат" х, до поворота бывший одним из потомков w, теперь черный. Таким путем случай 1 приводится к случаю 2, 3 или 4.
Случаи 2, 3 и 4 возникают при черном узле w и отличаются друг от друга цветами дочерних по отношению к w узлов.
Случай 2: узел w черный, оба его дочерних узла черные.
В этом случае (строки 10-11 процедуры RB_Delete_Fixup и рис. 13б) оба дочерних узла w черные. Поскольку узел w также черный, мы можем забрать черную окраску у х и w, сделав х единожды черным, a w - красным. Для того чтобы компенсировать удаление черной окраски у х и w, мы можем добавить дополнительный черный цвет узлу р[х], который до этого мог быть как красным, так и черным. После этого будет выполнена следующая итерация цикла, в которой роль х будет играть текущий узел р[х]. Заметим, что если мы переходим к случаю 2 от случая 1, новый узел х - красно-черный, поскольку исходный узел р[х] был красным. Следовательно, значение с атрибута color нового узла х равно red и цикл завершается при проверке условия цикла. После этого новый узел х окрашивается в обычный черный цвет в строке 23.
Случай 3: узел w черный, его левый дочерний узел красный, а правый - черный.
В этом случае (строки 13-16 процедуры RB_Delete_Fixup и рис. 13в) узел w черный, его левый дочерний узел красный, а правый - черный. Мы можем обменять цвета w и left[w], а затем выполнить правый поворот вокруг w без нарушения каких-либо красно-черных свойств. Новым "братом" узла х после этого будет черный узел с красным правым дочерним узлом, и таким образом мы привели случай 3 к случаю 4.
Случай 4: узел w черный, его правый дочерний узел красный.
В этом случае (строки 17-21 процедуры RB__Delete_Fixup и рис. 13г) узел w черный, а его правый дочерний узел - красный. Выполняя обмен цветов и левый поворот вокруг р[х], мы можем устранить излишнюю черноту в х, делая его просто черным, без нарушения каких-либо красно-черных свойств. Присвоение х указателя на корень дерева приводит к завершению работы при проверке условия цикла при следующей итерации.
Поиск узла с заданным ключом
Для поиска узла с заданным ключом в красно-черном дереве используется следующая процедура Tree_Search, которая получает в качестве параметров указатель на корень красно-черного дерева и ключ k, а возвращает указатель на узел с этим ключом (если таковой существует; в противном случае возвращается значение NIL).
TREE_SEARCH(x, k)
1 if 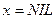 или
или 
2 then return x
3 if 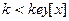
4 then return TREE_SEARCH(left[x], k)
5 else return TREE_SEARCH(right[x], k)
Процедура поиска начинается с корня дерева и проходит вниз по дереву. Для каждого узла х на пути вниз его ключ key [ x ] сравнивается с переданным в качестве параметра ключом k. Если ключи одинаковы, поиск завершается. Если k меньше key [ x ], поиск продолжается в левом поддереве х; если больше - то поиск переходит в правое поддерево. Так, на рис. 14 для поиска ключа 13 мы должны пройти следующий путь от корня: 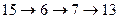 . Узлы, которые мы посещаем при рекурсивном поиске, образуют нисходящий путь от корня дерева, так что время работы процедуры Tree_Search равно О( h ), где h — высота дерева [3].
. Узлы, которые мы посещаем при рекурсивном поиске, образуют нисходящий путь от корня дерева, так что время работы процедуры Tree_Search равно О( h ), где h — высота дерева [3].
Ту же процедуру можно записать итеративно, "разворачивая" оконечную рекурсию в цикл while.

Рис. 14. Запросы в бинарном дереве поиска
Iterative_Tree_Search(x, k)
1 while 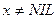 и
и 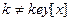
2 do if 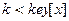
3 then 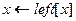
4 else 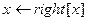
5 return x
Поиск минимума и максимума
Элемент с минимальным значением ключа легко найти, следуя по указателям left от корневого узла до тех пор, пока не встретится значение NIL. Так, на рис. 14, следуя по указателям left, мы пройдем путь 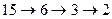 до минимального ключа в дереве, равного 2. Вот как выглядит реализация описанного алгоритма:
до минимального ключа в дереве, равного 2. Вот как выглядит реализация описанного алгоритма:
Tree_Minimum(x)
1 while 
2 do 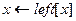
3 return x
Свойство бинарного дерева поиска гарантирует корректность процедуры Tree_Minimum. Поскольку в правом поддереве не может быть узла с ключом, меньшим key[x], а все ключи в узлах левого поддерева не превышают key[x], узел с минимальным значением ключа находится в поддереве, корнем которого является узел left[x] [3].
Алгоритм поиска максимального элемента дерева симметричен алгоритму поиска минимального элемента:
Tree_Maximum(x)
1 while 
2 do 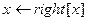
3 return x
Дата добавления: 2020-12-12; просмотров: 159; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
