Карта индивидуальных достижений
Гаджиева Радмила
Пособие для подготовки к ЕГЭ
для обучающихся 10-11 классов
по теме показательная функция

Математика
Пособие для подготовки к единому государственному экзамену по теме "Показательная функция"
Автор: Гаджиева Радмила Чергезовна
Рецензент: Оганисян Ирина Михайловна
Дата создания: октябрь 2020г. - январь 2021г.
Сборник предназначен для подготовки к единому государственному экзамену по математике и содержит 3 части, составленных в соответствии с проектом демоверсии КИМ ЕГЭ по математике профильного уровня.
Пособие состоит из трех частей. Первая часть включают в себя 11 заданий, вторая часть – 10 заданий, а третья - 13 заданий.
Все задачи даны с решениями, позволяющими проверить полноту и точность Ваших рассуждений.
В книге дана карта индивидуальных достижений обучающегося, которую можно использовать для отслеживания динамики результативности выполнения экзаменационных заданий
Если Вы собираетесь поступить в ВУЗ на техническую или экономическую специальность и Вам нужен высокий балл на ЕГЭ по математике, эта книга для Вас.

Оглавление
1.Введение…………………………………………………………………............3
2. Карта индивидуальных достижений…………………………………………..6
3.Свойства…………………………………………………………………………4
4. Решение задач…………………………………………………………………..5
5. Ответы…………………………………………………………………………..7
Введение
Изучение темы «Показательная функция» в курсе алгебры и начала анализа предусматривает знакомство учащихся с вопросами:
Обобщение понятия о степени; понятие о степени с иррациональным показателем; решение иррациональных уравнений и их систем; показательная функция, ее свойства и график; основные показательные тождества:  ,
, 
тождественные преобразования показательных выражений; решение показательных уравнений, неравенств и систем; понятие об обратной функции; функция, ее свойства и график;
Основная цель – привести в систему и обобщить имеющиеся у учащихся сведения о степени, ознакомить их с показательной функцией и ее свойствами, научить решать несложные показательные уравнения, их системы (содержащие также и иррациональные уравнения).
Рассматриваются свойства и график показательной функции. Систематизация свойств указанной функции осуществляется в соответствии с принятой схемой исследования функций. Приведен краткий обзор свойств степенной функции в зависимости от различных значений показателя р.
Особое внимание уделяется показательной функции как той математической модели, которая находит наиболее широкое применение при изучении процессов и явлений окружающей действительности. Рассматриваются примеры различных процессов (например, радиоактивный распад, изменение температуры тела); показывается, что решение дифференциальных уравнений, описывающих эти процессы, является показательная функция. В связи с этим для показательной функции дается формула производной, вывод которой проводится с привлечением интуитивных представлений учащихся.
В ходе изучения свойств показательной функцией учащиеся систематически решают простейшие показательные уравнения и неравенства, а также иррациональные уравнения. По мере закрепления соответствующих умений целесообразно также предлагать им уравнения и неравенства, сводящиеся к простейшим в результате несложных тождественных преобразований.
Появление вычислительной техники в школе открыло возможности, которые связаны с интеграцией новых информационных технологий в учебный процесс по различным школьным предметам. В настоящее время применение различных видов прикладного программного обеспечения носит преимущественно эпизодический характер.
Свойства функции:
1) Областью определения функции является множество всех действительных чисел R.
2) Множеством значений функции являются все положительные числа, т.е. промежуток 
3) Наименьшего и наибольшего значений функция не имеет.
4) Функция не является ни нечетной, ни четной. Имеет общий вид.
5) Функция непериодическая.
6) График функции пересекает координатную ось Oy в точке (0; 1).
7) Функция не имеет нулей.
8) При a>1 функция возрастает на всей числовой прямой; при 0<а<1 функция убывает на множестве R.
9) Функция принимает положительные значения на всей области определения.
Формулы:
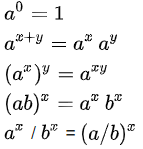
Карта индивидуальных достижений
Отметьте верно выполненные Вами задания и занесите ответы в таблицу.
| Часть Задания | Часть 1 | Часть 2 | Часть 3 |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 | - | ||
| 12 | - | - | |
| 13 | - | - | |
| 14 | - | - | - |
| 15 | - | - | - |
Задачи
1 часть
1. Найдите наименьшее значение функции 
2. Найдите точку максимума функции 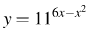
3. Найдите точку минимума функции 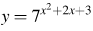
4. Найдите наименьшее значение функции 
5. Найдите наибольшее значение функции 
6. Решите уравнение: 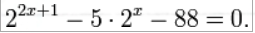
7. Решите уравнение: 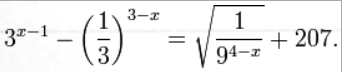
8. Решите уравнение: 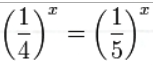
9. Решите уравнение: 
10. Решите уравнение: 
11. Решите уравнение: 
2 часть
1. Решите неравенство: 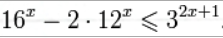
2. Решите неравенство: 
3. Решить неравенство 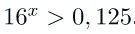
4. Решить неравенство: 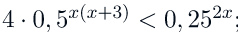
5. Решить неравенство: 
6. Решить неравенство: 
7. Решить неравенство: 
8. Решить неравенство: 
9. Решить неравенство: 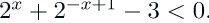
10. Решить неравенство: 
3 часть
1. Решите неравенство: 
2. Решите неравенство: 
3. Решите неравенство: 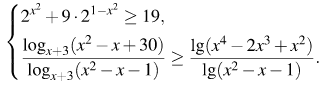
4. Решите неравенство: 
5. Решить неравенство: 
6. Решить неравенство: 
7. Решить неравенство: 
8. Решить неравенство: 
9. Решить неравенство: 
10. Решить неравенство: 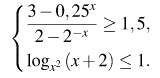
11. Решить неравенство: 
12. Решить неравенство: 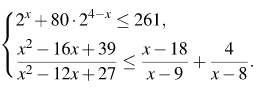
13. Решить неравенство: 
Ответы
1 часть
1. Решение:
Поскольку функция  возрастающая, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения выражение
возрастающая, заданная функция достигает наименьшего значения в той же точке, в которой достигает наименьшего значения выражение 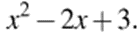 Квадратный трехчлен
Квадратный трехчлен  с положительным старшим коэффициентом достигает наименьшего значения в точке
с положительным старшим коэффициентом достигает наименьшего значения в точке 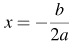 в нашем случае — в точке 1. Значение функции в этой точке равно
в нашем случае — в точке 1. Значение функции в этой точке равно 
Ответ: 49
2. Решение:
Поскольку функция  возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение
возрастающая, заданная функция достигает максимума в той же точке, в которой достигает максимума выражение 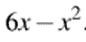 Квадратный трехчлен
Квадратный трехчлен  с отрицательным старшим коэффициентом достигает максимума в точке
с отрицательным старшим коэффициентом достигает максимума в точке 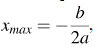 в нашем случае — в точке 3.
в нашем случае — в точке 3.
Ответ: 3.
3. Ответ: -1
4. Ответ: 16.
5. Ответ: 9.
6. Решение:
используем приведенные выше формулы и подстановку:  Уравнение тогда принимает вид:
Уравнение тогда принимает вид:  Дискриминант полученного квадратного уравнения положителен:
Дискриминант полученного квадратного уравнения положителен: 
Это означает, что данное уравнение имеет два корня. Находим их: 
Переходя к обратной подстановке, получаем:  Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе:
Второе уравнение корней не имеет, поскольку показательная функция строго положительна на всей области определения. Решаем второе: 
С учетом сказанного в теореме 1 переходим к эквивалентному уравнению: x = 3. Это и будет являться ответом к заданию.
Ответ: x = 3.
7.Решение:
ограничений на область допустимых значений у уравнения нет, так как подкоренное выражение имеет смысл при любом значении x (показательная функция y = 94-x положительна и не равна нулю).
Решаем уравнение путем равносильных преобразований с использованием правил умножения и деления степеней:




Ответ: x = 6.
8. Решение:
обе части исходного уравнения можно поделить на 0,2x. Данный переход будет являться равносильным, поскольку это выражение больше нуля при любом значении x (показательная функция строго положительна на своей области определения). Тогда уравнение принимает вид:

Ответ: x = 0
9. Решение:
упрощаем уравнение до элементарного путем равносильных преобразований с использованием приведенных в начале статьи правил деления и умножения степеней:


Деление обеих частей уравнения на 4x, как и в предыдущем примере, является равносильным преобразованием, поскольку данное выражение не равно нулю ни при каких значениях x.
Ответ: x = 0
10. Решение:
функция y = 3x, стоящая в левой части уравнения, является возрастающей. Функция y = —x-2/3, стоящая в правой части уравнения, является убывающей. Это означает, что если графики этих функций пересекаются, то не более чем в одной точке. В данном случае нетрудно догадаться, что графики пересекаются в точке x = -1. Других корней не будет.
Ответ: x = -1.
11.Решение:
упрощаем уравнение путем равносильных преобразований, имея в виду везде, что показательная функция строго больше нуля при любом значении x и используя правила вычисления произведения и частного степеней, приведенные в начале статьи:



Ответ: x = 2
2 часть
1. Решение:
представим исходное неравенство в виде:

Разделим обе части этого неравенства на 32x, при этом (в силу положительности функции y = 32x) знак неравенства не изменится: 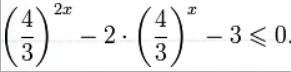
Воспользуемся подстановкой:
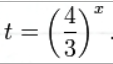
Тогда неравенство примет вид:
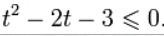
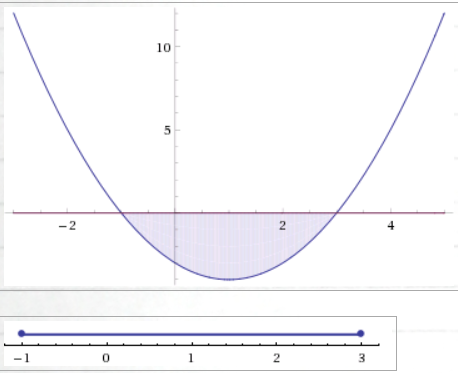
Итак, решением неравенства является промежуток: 
переходя к обратной подстановке, получаем: 
Левое неравенства в силу положительности показательной функции выполняется автоматически. Воспользовавшись известным свойством логарифма, переходим к эквивалентному неравенству:

Поскольку в основании степени стоит число, большее единицы, эквивалентным (по теореме 2) будет переход к следующему неравенству:

Итак, окончательно получаем ответ: 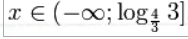
2. Решение:
Разделим обе части неравенства на положительное выражение 
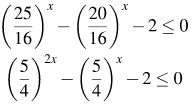
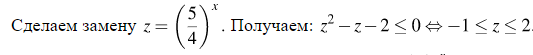
Возвращаясь к исходной переменной, получаем: 
Ответ: 
3.
Решение:
Перепишем неравенство следующим образом:


Так как  – возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:
– возрастающая функция, то знак неравенства остается без изменения при переходе к новому неравенству:

Ответ: 
4. Решение:
Перепишем неравенство следующим образом:
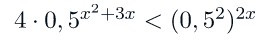
Заметим, что 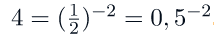

В силу того, что основание степени (0,5) меньше 1, то есть мы имеем дело с убывающей функцией, переходим к следующему неравенству (не забывая поменять знак < на >):

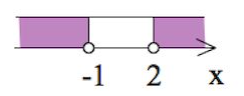

Ответ: 
5. Решение:
Вынесем за скобку 
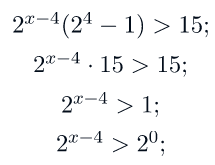
Тогда переходим к следующему неравенству (в силу того, что основание степени больше 1, знак неравенства не меняется):
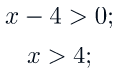
Ответ: 
6. Решение:
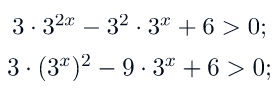
Разделим обе части неравенства на 3:
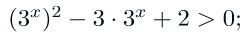
Мы видим квадратное неравенство относительно 3^x, которое будем решать методом интервалов.
Имеем:



Ответ: 
7. Ответ: 
8. Ответ: 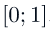
9. Ответ: 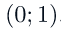
10. Ответ: 
Уровень 3
1. Решение:
Пусть 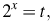 тогда неравенство примет вид
тогда неравенство примет вид  Решим это неравенство методом интервалов:
Решим это неравенство методом интервалов: 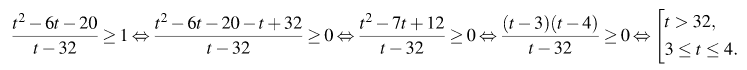
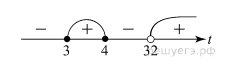
Возвращаясь к исходной переменной, получаем: 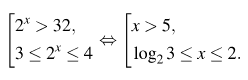
Ответ: 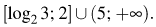
2. Решение:
Решим первое неравенство:
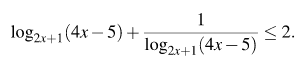
Сделаем замену 

Если 
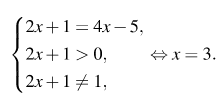
Если 

Множество решений первого неравенства: 
Решим второе неравенство. Разделим правую и левую части на 

Сделаем замену  Получаем:
Получаем: 
Решением системы является пересечение решений двух неравенств. Учитывая, что  находим решение системы:
находим решение системы: 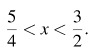
Ответ: 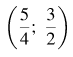
3. Решение:
Решим первое неравенство системы.
Пусть  тогда данное неравенство принимает вид
тогда данное неравенство принимает вид 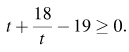
Учитывая условие  получаем
получаем 
Имеем:

Множество решения первого неравенства системы: 
Решим теперь второе неравенство системы.
Заметим, что при 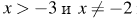 исходное неравенство равносильно неравенству:
исходное неравенство равносильно неравенству:

Положив в последнем неравенстве  получаем:
получаем:

Таким образом, имеем: 
Учитывая то, что 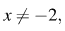 получаем множество решений второго неравенства:
получаем множество решений второго неравенства:
 Принимая во внимание, что
Принимая во внимание, что 
находим решение данной системы: 
Ответ: 
4. Ответ: 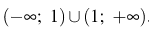
5. Ответ: 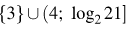
6. Ответ: 
7. Ответ: 
8. Ответ: 
9. Ответ: 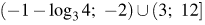
10. Ответ: 
11. Ответ: 
12. Ответ: 
13. Ответ: 
Математика
Сборник заданий
по теме «Показательная функция»
Автор: Гаджиева Радмила Чергезовна
Рецензент: Оганисян Ирина Михайловна
Задания взяты с сайта РешуЕГЭ
Дата создания: январь 2021
Дата добавления: 2021-02-10; просмотров: 60; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
