Вычисление площади плоской фигуры
Определенный интеграл
Вычисление определенного интеграла
Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных средств математического анализа. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и т.д. сводится к вычислению определенного интеграла.
Пусть на отрезке [a, b] задана непрерывная функция  . Разделим отрезок
. Разделим отрезок  на п произвольных частей точками
на п произвольных частей точками 
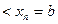 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке  произвольную точку
произвольную точку 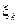 и найдем длину каждого такого отрезка:
и найдем длину каждого такого отрезка: 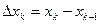 .
.
Определение 1. Интегральной суммой для функции  на отрезке
на отрезке 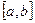 называется сумма следующего вида
называется сумма следующего вида  ,
,
Определение 2. Определенным интегралом от функции  на отрезке
на отрезке 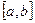 (или в пределах от а до b) называется предел интегральной суммы (если он существует) при условии, что длина наибольшего из элементарных отрезков (
(или в пределах от а до b) называется предел интегральной суммы (если он существует) при условии, что длина наибольшего из элементарных отрезков (  ) стремится к нулю:
) стремится к нулю:
 .
.
Теорема существования определенного интеграла
Если функция  непрерывна на отрезке
непрерывна на отрезке 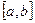 , то предел интегральной суммы существует и не зависит от способа разбиения отрезка
, то предел интегральной суммы существует и не зависит от способа разбиения отрезка 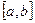 на элементарные отрезки и от выбора точек
на элементарные отрезки и от выбора точек 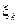 .
.
При этом числа а и b соответственно называются нижним и верхним пределами интегрирования.
Если  на
на 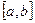 , то определенный интеграл
, то определенный интеграл  с геометрической точки зрения представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями
с геометрической точки зрения представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями 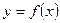 ,
, 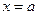 ,
, 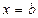 ,
,  (рис. 1).
(рис. 1).
 |
Рис. 1
Приведем далее без доказательства основные свойства определенного интеграла, непосредственно вытекающие из определения:
1.  ;
;
2.  ;
;
3. 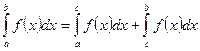 ;
;
4.  ;
;
5. 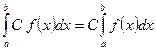 , где С – постоянная величина;
, где С – постоянная величина;
6. Оценка определенного интеграла. Если т и М – наименьшее и наибольшее значения функции  на отрезке
на отрезке  и
и  , то
, то
 ;
;
7. Если на отрезке  функции
функции  и
и  удовлетворяют условию
удовлетворяют условию  , то
, то
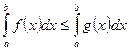 ;
;
8.Теорема о среднем. Если функция  непрерывна на
непрерывна на 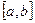 , то на этом отрезке имеется такая точка x, что справедливо следующее равенство:
, то на этом отрезке имеется такая точка x, что справедливо следующее равенство:
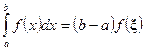 .
.
Рассмотрим правила вычисления определенного интеграла.
Формула Ньютона – Лейбница
Если  есть какая-либо первообразная от непрерывной функции
есть какая-либо первообразная от непрерывной функции  , то справедлива формула
, то справедлива формула
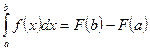 .
.
Она называется формулой Ньютона – Лейбница или основной формулой интегрального исчисления. Эта формула дает практически удобный метод вычисления определенных интегралов в том случае, если известна первообразная подынтегральной функции.
Пример 1. Вычислить интеграл  .
.
 .
.
Пример 2. Вычислить интеграл  .
.
 .
.
Пример 3. Вычислить интеграл  .
.
 .
.
Простейшие методы вычисления определенных интегралов
Замена переменной в определенном интеграле
Пусть дан интеграл
 ,
,
где функция  непрерывна на отрезке
непрерывна на отрезке 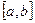 . Введем новую переменную t формулой
. Введем новую переменную t формулой
 .
.
Если
1)  ,
,  ;
;
2) 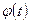 и
и  непрерывны на отрезке
непрерывны на отрезке 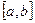 ;
;
3)  определена и непрерывна на отрезке
определена и непрерывна на отрезке 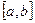 , то
, то
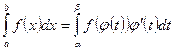 .
.
Отметим, что при вычислении определенного интеграла в данном случае мы не возвращаемся к старой переменной.
Пример 4. Вычислить интеграл 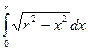 .
.
Сделаем замену переменной  , тогда
, тогда  . Определим новые пределы:
. Определим новые пределы: 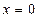 при
при 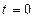 ,
,  при
при 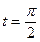 . Следовательно,
. Следовательно,

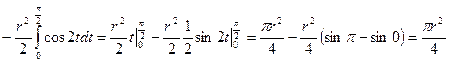 .
.
Пример 5. Вычислить интеграл  .
.
Сделаем замену переменной  ,
,  . Определим новые пределы:
. Определим новые пределы: 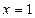 при
при 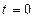 ,
,  при
при  . Следовательно,
. Следовательно,
 .
.
Интегрирование по частям
Если  и
и 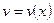 - непрерывно дифференцируемые функции на отрезке
- непрерывно дифференцируемые функции на отрезке 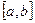 , то можно воспользоваться следующей формулой:
, то можно воспользоваться следующей формулой:
 .
.
Пример 6. Вычислить интеграл  .
.
Пусть  ,
,  , откуда
, откуда  ,
,  . Тогда
. Тогда
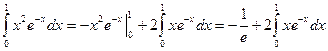 .
.
Применим формулу интегрирования по частям еще раз. Положим 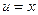 ,
,  , откуда
, откуда  ,
,  . Следовательно,
. Следовательно,

В некоторых случаях при вычислении определенных интегралов удобно пользоваться формулами вида:
1) если  - нечетная функция, т.е.
- нечетная функция, т.е. 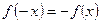 , то
, то
 ;
;
2) если  - четная функция, т.е.
- четная функция, т.е. 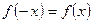 , то
, то
 .
.
Пример 7. Вычислить интеграл  .
.
Подынтегральная функция – нечетная, следовательно,
 .
.
Пример 8. Вычислить интеграл  .
.
Подынтегральная функция – четная, поэтому  . Интегрируя по частям, полагая
. Интегрируя по частям, полагая 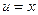 ,
,  , откуда получаем
, откуда получаем  ,
,  . Следовательно,
. Следовательно,

 .
.
Вычисление площади плоской фигуры
Площадь криволинейной трапеции, ограниченной кривой 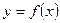
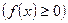 , прямыми
, прямыми 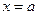 и
и 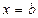 , и отрезком
, и отрезком 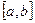 оси Ох, вычисляется по формуле:
оси Ох, вычисляется по формуле:
 .
.
Площадь фигуры, ограниченной кривыми 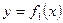 ,
, 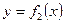
 и прямыми
и прямыми 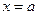 ,
, 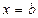 , вычисляется по формуле:
, вычисляется по формуле:
 .
.
Пример 9. Найти площадь плоской фигуры, ограниченной параболой  и гиперболой
и гиперболой  .
.

Рис. 3
Найдем точки пересечения параболы и гиперболы, для чего решим совместно уравнения этих кривых:

или
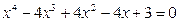 .
.
Левую часть последнего уравнения можно разложить на множители
 ,
,
откуда 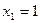 ,
,  и
и  ,
,  . Таким образом, заданные кривые пересекаются в точках
. Таким образом, заданные кривые пересекаются в точках  и
и  (см. рис. 3). Следовательно,
(см. рис. 3). Следовательно,
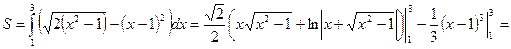
 .
.
Дата добавления: 2021-02-10; просмотров: 81; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
