Основные свойства плотности распределения
Глава 2. Случайные величины, их распределение и числовые характеристики
Дискретные и непрерывные случайные величины
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, не известно заранее, какое именно. Различают величины дискретного и непрерывного типа. Возможные значения дискретной величины могут быть заранее перечислены. Возможные значения непрерывной величины не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток. Приведем примеры дискретных случайных величин:
– число появлений герба при 3-х бросаниях монеты: 0, 1, 2, 3;
– число отказавших элементов в приборе, состоящем из пяти элементов-0,1,2,3,4,5;
– число сбитых в воздушном бою самолетов - 0,1,2,…,  ; где
; где 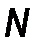 - общее число боевых самолетов.
- общее число боевых самолетов.
Примеры непрерывных случайных величин:
– абсцисса (ордината) попадания при выстреле;
– расстояние от точки попадания до центра мишени;
– ошибка измерителя высоты;
– время безотказной работы радиолампы.
Будем обозначать случайные величины большими буквами  , а их возможные значения - соответствующими малыми буквами. Например,
, а их возможные значения - соответствующими малыми буквами. Например, 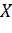 - число попаданий при 3-х выстрелах; возможные значения -
- число попаданий при 3-х выстрелах; возможные значения -  .
.
Рассмотрим дискретную случайную величину 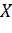 с возможными значениями
с возможными значениями 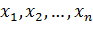 .
. 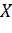 может принимать любое из этих значений с некоторой вероятностью. В результате опыта произойдет одно из полной группы событий
может принимать любое из этих значений с некоторой вероятностью. В результате опыта произойдет одно из полной группы событий 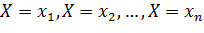 . Вероятности этих событий обозначим буквой
. Вероятности этих событий обозначим буквой 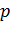 с соответствующими индексами –
с соответствующими индексами –
|
|
|
 .
.
Так как эти несовместные события образуют полную группу, то 
 . Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана, с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий
. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана, с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий 

 . Этим мы установим так называемый закон распределения случайной величины.
. Этим мы установим так называемый закон распределения случайной величины.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину будем говорить, что она подчинена данному закону распределения.
Формой задания закона является таблица
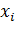
| 
| 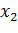
| 
| 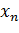
|

| 
| 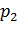
| 
| 
|
Эту таблицу мы будем называть рядом распределения случайной величины X.
Графическое изображение ряда распределения называется многоугольником или полигоном распределения 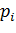 . Многоугольник распределения - также одна из форм закона распределения.
. Многоугольник распределения - также одна из форм закона распределения.
Функция распределения
Мы рассмотрели закон распределения дискретной случайной величины. Для непрерывной случайной величины такую характеристику построить нельзя. Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток (несчетное множество). Для непрерывной случайной величины не существует ряда распределения, как он существует для дискретной величины. Но различные области возможных значений случайных величин все же не является одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для прерывной.
|
|
|
Для количественной характеристики, этого распределения вероятностей удобно воспользоваться не вероятностью события  , а вероятностью события
, а вероятностью события 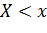 , где
, где  – некоторая текущая переменная. Вероятность этого события есть некоторая функция от
– некоторая текущая переменная. Вероятность этого события есть некоторая функция от 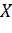 . Эта функция называется функцией распределения случайной величины
. Эта функция называется функцией распределения случайной величины 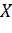 и обозначается
и обозначается  ,
,  .
.
Функцию распределения  иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения является универсальной характеристикой случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных.
иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения является универсальной характеристикой случайной величины. Она существует для всех случайных величин: как дискретных, так и непрерывных.
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т. е. является одной из форм закона распределения.
|
|
|
Сформулируем общие свойства функции распределения:
1)  - неубывающая, т.е. при
- неубывающая, т.е. при  ,
,  ;
;
2)  ;
;
3)  .
.
Пример. Производится четыре независимых опыта, в каждом из которых может появиться или не появиться событие 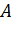 . Построить функцию распределения числа появлений события
. Построить функцию распределения числа появлений события 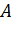 .
.
Решение. Обозначим через 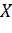 - число появлений события
- число появлений события 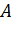 в четырех опытах. Эта величина имеет ряд распределения
в четырех опытах. Эта величина имеет ряд распределения
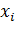
| 0 | 1 | 2 | 3 | 4 |
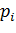
| 0.2401 | 0.4116 | 0.2646 | 0.0756 | 0.0081 |
Построим функцию распределения случайной величины 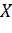 .
.
1) при   0 0  =0
2) при 0< =0
2) при 0<   1 1  =0,2401
3) при 1< =0,2401
3) при 1<  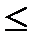 2 2  =0,6517
4) при 2< =0,6517
4) при 2<  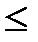 3 3  =0,9163
5) при 3< =0,9163
5) при 3<   4 4  =0,991
6) при 4> =0,991
6) при 4>   =1 =1
|
Функция распределения любой дискретной величины есть разрывная ступенчатая функция, разрывы которой происходят в точках, соответствующих возможным значениям случайной величины.
С увеличением числа возможных значений случайной величины и уменьшением интервалов между ними число разрывов становится больше, а сами разрывы меньше; ступенчатая кривая становится более плавной; случайная величина приближается к непрерывной случайной величине, а ее функция распределения - к непрерывной функции. На практике обычно функция распределения для непрерывной случайной величины представляет собой функцию, непрерывную во всех точках.
|
|
|
Плотность распределения
Пусть имеется непрерывная случайная величина 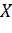 с функцией распределения
с функцией распределения  , которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от
, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от  до
до  .
.
 ,
,
т.е. приращение функции распределения на этом участке.
Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать  . В пределе получим производную от функции распределения
. В пределе получим производную от функции распределения
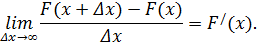
Обозначим 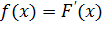 . Функция
. Функция  - производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины
- производная функции распределения, характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (плотностью вероятности) непрерывной случайной величины 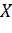 . Иногда
. Иногда  называют дифференциальной функцией распределения или дифференциальным законом распределения величины
называют дифференциальной функцией распределения или дифференциальным законом распределения величины 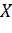 .
.
Плотность распределения так же, как и функция распределения есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной: она существует только для непрерывных случайных величин.
Выразим вероятность попадания величины 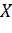 на отрезок от
на отрезок от  до
до  через плотность распределения. Очевидно, оно равно
через плотность распределения. Очевидно, оно равно  .
.
Формула 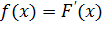 выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
выражает плотность распределения через функцию распределения. Зададимся обратной задачей: выразить функцию распределения через плотность. По определению
 , откуда
, откуда  .
.
Основные свойства плотности распределения
1. Плотность распределения есть неотрицательная функция 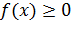 ;
;
2. Интеграл в бесконечных пределах от плотности распределения равен 1:
 ;
;
3.  .
.
Рассмотрим несколько примеров.
Пример 1. Функция распределения непрерывной случайной величины  задана выражением:
задана выражением:

Найти плотность распределения f ( x ). Найти вероятность попадания величины 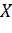 на участок от 0,25 до 0,5.
на участок от 0,25 до 0,5.
Решение. Плотность распределения выражается формулой
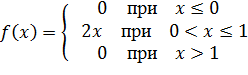

Замечание. Плотность распределения вероятностей – это производная от функции распределения, поэтому  часто называют дифференциальной функцией распределения. Так как
часто называют дифференциальной функцией распределения. Так как  , ее называют интегральной функции распределения.
, ее называют интегральной функции распределения.
Дата добавления: 2021-02-10; просмотров: 83; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
