Бинарные алгебраические операции
Лекция 1
Комплексные числа и действия над ними
Понятие комплексного числа
Определение. Комплексным числом называется выражение вида z = x + i y , где x, y – некоторые действительные числа; i – символ, называемый мнимой единицей, обладающий свойством i2 = -1.
Представление числа z имеет свойство коммутативности: x + i y = i y + x . Числа x и y называются соответственно действительной и мнимой частями комплексного числа z :
x = Re z, y = Im z .

 Модулем z комплексного числа z называется действительное неотрицательное
Модулем z комплексного числа z называется действительное неотрицательное
число, определяемое выражением


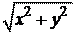 z = .
z = .
 Число
Число
z = x + i(- y) = x - iy
называют комплексно сопряжённым с числом z . Если
y = 0 , число z считается действительным; числа вида 0 + i y º i y
называются чисто
мнимыми. Два комплексных числа
z1 = x1 + i y1 и
z2 = x2 + i y2
считаются равными,
если равны их действительные и мнимые части соответственно:
z1 = z2 Û x1 = x2, y1 = y2 .
Принимается, что для символа i справедливы коммутативный по отношению к умножению и дистрибутивный законы:
i y = yi ,
i( y1 + y2 ) = i y1 + iy2 .
Множество всех комплексных чисел обозначается символом 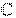 .
.
2. Арифметические операции с комплексными числами
1. Сумма и разность двух комплексных чисел
определяется по формуле
z1 = x1 + i y1 и
z2 = x2 + i y2
z1 ± z2 = x1 ± x2 + i( y1 ± y2 ) .
2. Умножение комплексных чисел производится, как умножение многочленов с учётом перечисленных свойств числа i :
|
|
|
z1 × z2 = (x1 + i y1) × (x2 + i y2 ) = x1x2 + i y1x2 + x1i y2 + i y1i y2 =
= (x1x2 - y1y2 ) + i( y1x2 + x1y2 ).
Заметим, что произведение числа на комплексно сопряжённое с ним есть действительное число, равное квадрату его модуля:


 z× z = (x + iy) × (x - i y) = x2 + y2 = z 2 . (1)
z× z = (x + iy) × (x - i y) = x2 + y2 = z 2 . (1)
3. Частное двух комплексных чисел
z = z1
 z2
z2
по определению есть решение
уравнения
z× z2 = z1.
а) При делении комплексного числа имеем:
z1 на действительное
x2 , очевидно,
 z = z1
z = z1
= x1 + i y1 =
x1 + i y1 .


 x2 x2 x2 x2
x2 x2 x2 x2
б) Деление на произвольное комплексное число
z2 ¹ 0
можно свести к
делению на действительное число, домножив и числитель, и знаменатель на число, комплексно сопряжённое знаменателю, и воспользовавшись тождеством (1.1):


 z = z1
z = z1
z2
= z1 z2
 z2 z2
z2 z2
= z1 z2


 z2 2
z2 2
. (2)
Пример.
2 + 3i

3 + 4i
= (2 + 3i)(3 - 4i) = 2 × 3 + 3i× 3 - 2 × 4i - 3i × 4i =

 (3 + 4i)(3 - 4i) 32 + 42
(3 + 4i)(3 - 4i) 32 + 42
= 6 -12i2 + 9i - 8i = 6 +12 + i = 18 + 1
 i .
i .
25 25 25 25
|
|
|
Несложно проверить, что введенные выше операции сложения и умножения над комплексными числами обладают свойствами:
а) Ассоциативности
(z1 + z2) + z3 = z1 + (z2 + z3); (z1 × z2)z3 = z1(z2 × z3) .
б) Коммутативности
z1 + z2 = z2 + z1;
z1 × z2 = z2 × z1.
в) Дистрибутивности
z1(z2 + z3 ) = z1z2 + z1z3 .
Перечислим также свойства операции комплексного сопряжения:




z = z , z ± z = z ± z

 |  |
, z × z = z × z

, æ z1 ö = z1 .


 1 2 1 2
1 2 1 2
1 2 1 2
ç ÷

|
3. Геометрическое изображение комплексных чисел на плоскости
Выберем на плоскости прямоугольную систему координат. Всякое комплексное
число z = x + iy
изображается точкой на плоскости с координатами x и y (рис.1.1).
 Такое соответствие между комплексными числами и точками плоскости является взаимно однозначным. При этом действительные числа изображаются точками оси абсцисс, а чисто мнимые – точками оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат – мнимой осью.
Такое соответствие между комплексными числами и точками плоскости является взаимно однозначным. При этом действительные числа изображаются точками оси абсцисс, а чисто мнимые – точками оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат – мнимой осью.
|
|
|
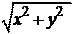 Плоскость, на которой изображают комплексные числа, называют комплексной плоскостью. Комплексное число z изображается также вектором с началом в точке O и проекциями x и y на координатные оси. Длина вектора z равна
Плоскость, на которой изображают комплексные числа, называют комплексной плоскостью. Комплексное число z изображается также вектором с началом в точке O и проекциями x и y на координатные оси. Длина вектора z равна
 – модулю комплексного числа, в этом состоит геометрический смысл модуля комплексного числа | z |. Из
– модулю комплексного числа, в этом состоит геометрический смысл модуля комплексного числа | z |. Из




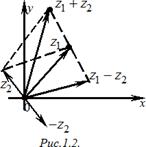
 геометрической интерпретации комплексных чисел следует ряд полезных выводов и неравенств (рис.1.2).
геометрической интерпретации комплексных чисел следует ряд полезных выводов и неравенств (рис.1.2).


 1) Re z1 £
1) Re z1 £
z1 , Im z1 £
z1 .

 2) z1 - z2
2) z1 - z2
– расстояние между точками
z1 и
z2 .


 3) z1 - z2
3) z1 - z2
£ z1 + z2
£ z1 + z2
(неравенства треугольника).
4. 



 Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа
Положение точки на комплексной плоскости z однозначно определяется
расстоянием точки от начала координат
r =| z |
и углом j между положительным
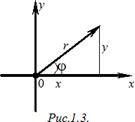 направлением действительной оси и вектором z (рис.1.3). Этот
направлением действительной оси и вектором z (рис.1.3). Этот
угол называется аргументом комплексного числа
z(z ¹ 0) , и
обозначается arg(z) . Для числа z=0 arg(z)
рис.1.3 видно, что
x = r cosj, y = r sin j.
не определен. Из
(3)
Следовательно, любое комплексное число
z ¹ 0
можно представить в виде
|
|
|
z = r(cosj + isinj).
(4)
Запись комплексного числа в виде (1.4) называется тригонометрической формой комплексного числа, в отличие от записи комплексного числа в виде z = x + i y , которая называется алгебраической формой комплексного числа. Для
нахождения аргумента комплексного числа надо решить систему уравнений
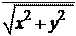
|
ï
í x
(5)
ïcosj=

|
Система (1.5) имеет бесконечно много решений, задаваемых формулой
 j = a + 2pk, k = 0,±1,± 2, где a – значение аргумента z, удовлетворяющее
j = a + 2pk, k = 0,±1,± 2, где a – значение аргумента z, удовлетворяющее
условию -p < a £ p. Это значение называется главным значением аргумента и обозначается arg z. Все значения аргумента данного комплексного числа задаются функцией, называемой многозначным аргументом:
 Argz = arg z + 2kp, k = 0,±1,± 2,
Argz = arg z + 2kp, k = 0,±1,± 2,
. (6)
Для главного значения аргумента справедливы соотношения:
ì y
 ïarctg x ,
ïarctg x ,
x > 0; (а)
ï

|
x
ï y
+ p, x < 0, y ³ 0; (б)

|
ï
(7)

|
|
ï 2
p

|
î 2
x = 0, y < 0. (д)



|
, то:
x 2 2
а) если точка лежит в I или IV

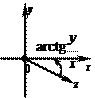
 четверти (x > 0), arg z = arctg y
четверти (x > 0), arg z = arctg y

 x
x
|
p y y
(рис.1.4a)
б) Если z лежит во второй четверти (x < 0, y ³ 0) , то
- 
 < arctg £ 0
< arctg £ 0
2 x
и arg z = p + arctg
 x
x
(рис.1.4б)

 в) если z находится в III четверти (x <0, y <0), то 0 < arctg y < p и
в) если z находится в III четверти (x <0, y <0), то 0 < arctg y < p и
 arg z = -p + arctg y
arg z = -p + arctg y
x
x 2
(рис.1.4в);
г) и д) варианты формулы (1.7) очевидны.
С помощью тригонометрической формы (1.4) комплексного числа несложно установить, как изменяются модуль и аргумент комплексного числа при умножении или делении на другое комплексное число, а также при возведении его в целую степень. Пусть
z1 = r1(cosj1 + isin j1), z2 = r2(cosj2 + isinj2) ,
тогда, используя формулы элементарной тригонометрии, получаем:
z1z2 = r1r2 (cos(j1 + j2 ) + i sin(j1 + j2 )), (8)
т.е. при умножении комплексных чисел их модули перемножаются, а аргументы складываются. Отсюда сразу получаем, что при делении на действительное число аргумент не изменяется, поскольку это равносильно умножению на обратное ему, также действительное число. Далее, поскольку
 z = r(cosj - isinj) = r(cos(-j) + isin(-j)) , (9)
z = r(cosj - isinj) = r(cos(-j) + isin(-j)) , (9)
то




 z1 = z1 z2 z2 z2 2
z1 = z1 z2 z2 z2 2
= r1r2 (cos(j1 - j2 ) + i sin(j1 - j2 )) =
 r22
r22
(10)
 = r1 (cos(j1 - j2 ) + i sin(j1 - j2 )),
= r1 (cos(j1 - j2 ) + i sin(j1 - j2 )),
r2
т.е. модуль частного двух комплексных чисел есть частное их модулей, а аргумент частного – разность аргументов. Из (1.8) и (1.10) следует формула, удобная для возведения комплексного числа в произвольную целую степень:
z n = r n (cos nj + i sin nj), n Î 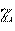 . (11)
. (11)
Замечание. Главное значение аргумента произведения или частного двух чисел
может отличаться от суммы или разности аргументов на
±2p.
4. Показательная форма комплексного числа
Полагая
r1 = r2 = r =1
в формулах (1.8), (1.10), (1.11), найдём, что выражение
cosj + isinj обладает свойствами показательной функции, в частности справедлива
формула Муавра:
(cosj + i sinj)n = (cos nj + i sin nj), n Î 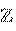 . (12) Более того, поскольку
. (12) Более того, поскольку
 d (cosj + i sinj) = -sinj + i cosj = i(cosj + i sinj) ,
d (cosj + i sinj) = -sinj + i cosj = i(cosj + i sinj) ,
dj
а также cos0 + isin 0 =1, выражение cosj + isinj имеет такое же разложение в ряд
Тейлора по степеням j , как и показательная функция
eij (экспонента с чисто
мнимым показателем), если считать правила дифференцирования показательной функции по действительному аргументу справедливыми и для экспоненты с комплексным коэффициентом в показателе (это будет показано позже). Поэтому
выражение cosj + isinj принимается за определение функции произвольном действительном j :
eij при
e ij = cosj + i sinj. (13)
Перечислим свойства функции
eij .
1. Периодичность с периодом T = 2p.
2. 
 e ij
e ij
3.
= 1.
 |
e ij = cosj - i sinj = e-ij . (14)
ij × ij i(j +j )
eij1 =

i(j -j )
ij n inj
4. e 1 e 2 = e
1 2 , ij
e 1 2
, (e ) = e
. (15)
e 2
Из (1.13) и (1.14) сложением и вычитанием получим формулы Эйлера:
eij + e-ij
 cosj =
cosj =
, sin
j = e ij - e-ij . (16)
 2 2i
2 2i
Используя (1.13), представление (1.4) комплексного числа можно переписать в виде, который называется показательной формой комплексного числа:
z = reij . (17)
В показательной форме удобно проводить операции умножения и деления комплексных чисел.
Замечание. С помощью формулы Муавра можно получить различные тригонометрические равенства. Получим формулы для cos3j,sin3j. Для этого
запишем равенство равенства
(cosj + isinj)3 = cos3j + isin3j. Преобразуем левую часть
cos3 j + 3i cos2 jsinj - 3cosjsin2 j - isin3 j = cos3j + isin3j .
Из условия равенства комплексных чисел находим:
cos3j = cos3 j - 3cosjsin2 j, sin3j = 3cos2 j×sinj - sin3 j.
После преобразований, учитывая, что cos2 j + sin2 j =1, получим искомые равенства
cos3j = 4cos3 j - 3cosj, sin3j = 3sinj - 4sin3 j.
6. Извлечение корня n-ой степени из комплексного числа
Пусть n – натуральное число, а z – заданное комплексное число. Определим
 = w так, что
= w так, что
Пусть
w =| w | e iy , тогда
wn = z . (18)
w n =| w |n e iny = z =| z | e i arg z . (19) Из равенства (1.19) следуют равенства

 wn =| z |,
wn =| z |,
ny = arg z + 2kp, k = 0, ±1, ±2 ,
второе из которых есть следствие многозначности аргумента. Выражая | w |
 получим
получим
и y ,
 | w |= n | z |,
| w |= n | z |,
y = arg z + 2kp,
 n
n
k = 0, ±1, ±2, ,
 где – обычный арифметический корень n-й степени из положительного числа.
где – обычный арифметический корень n-й степени из положительного числа.
Таким образом, для решений уравнения (1.18) имеем
 i arg z +2k p
i arg z +2k p

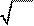 wk = (n z )k = n | z |e n , k = 0, ±1, ±2,
wk = (n z )k = n | z |e n , k = 0, ±1, ±2,
. (20)
 Выясним, сколько существует различных значений корня . Подставляя в
Выясним, сколько существует различных значений корня . Подставляя в
формулу (1.20)
k = 0,1, ,n -1, получим n различных значений
. Эти значения

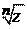 различны, так как разность аргументов каждых двух из них не кратна 2p. Поэтому,
различны, так как разность аргументов каждых двух из них не кратна 2p. Поэтому,
зная один корень
w0 , остальные можно получить последовательными поворотами
 на угол 2p против часовой стрелки. При всех остальных целых k по формуле (1.20)
на угол 2p против часовой стрелки. При всех остальных целых k по формуле (1.20)
 n
n
будут получаться значения, совпадающие с одним из корней при
k = 0,1, ,n -1.
Например, при k = n
получим то же значение, что и при
k = 0
и т.д. Таким образом,
корень n-й степени из произвольного комплексного числа значений, которые определяются формулой
 i arg z +2k p
i arg z +2k p
z ¹ 0
имеет ровно n

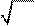 wk = (n z )k = n | z |e
wk = (n z )k = n | z |e
n , k = 0,1, , n -1. (21)
 Пример. Найти все различные значения корня .
Пример. Найти все различные значения корня .
Решение. Обозначим z = –27, тогда |z|=27, arg z = arg(-27) = p, имеем
 wk = 3 27 æ p + 2k p + i sin p + 2k p ö, k = 0,1, 2 .
wk = 3 27 æ p + 2k p + i sin p + 2k p ö, k = 0,1, 2 .
ç 3 3 ÷
è ø
Найдем значения
w k :
 k = 0, w = 3æcos p + i sin p ö = 3æ 1 + i3 ö ;
k = 0, w = 3æcos p + i sin p ö = 3æ 1 + i3 ö ;
0 ç 3 3 ÷
ç 2 2 ÷
è ø è ø
k =1, w1 = 3(cosp + isinp) = -3;
 k = 2, w = 3æcos 5 p + i sin 5 p ö = 3æ 1 - i3 ö .
k = 2, w = 3æcos 5 p + i sin 5 p ö = 3æ 1 - i3 ö .
2 ç 3 3 ÷
ç 2 2 ÷
è ø è ø
Изобразим эти числа на комплексной плоскости (рис.1.5). Точки вершины правильного треугольника.
w0, w1, w2 –
|
 Рис1.5.
Рис1.5.
7. Множества точек на комплексной плоскости
Комплексные числа можно рассматривать как элементы линейного
нормированного пространства с нормой
z =| z |. Расстояние между двумя

 комплексными числами
комплексными числами
z1 и
z2 определяется как норма их разности, т.е.

 r(z1, z2) = z1 - z2 . (22)
r(z1, z2) = z1 - z2 . (22)
 Из (22) следует, что уравнение
Из (22) следует, что уравнение
z - z0 = R
задаёт множество точек z плоскости,


 находящихся на расстоянии R от фиксированной точки
находящихся на расстоянии R от фиксированной точки
z0 , т.е. окружность
радиусом R с центром в точке
z0 . Соответственно, неравенство
z - z0 £ R
задаёт
круг радиусом R с центром в точке
z0 , а неравенство
z - z0 > R
– внешность этого

 круга. Двойное неравенство
круга. Двойное неравенство
R1 £
z - z0
£ R2
задаёт кольцо между окружностями

 радиусами
радиусами
R1 и
R2 с центром в точке
z0 .
Аналогичным образом, записывая условия на аргумент, действительную или мнимую часть комплексного числа, можно задавать некоторые множества точек. Например, уравнение arg z =a задаёт луч, выходящий из начала координат и образующий угол a с положительным направлением действительной оси; неравенство Im z £ b задаёт полуплоскость, ограниченную сверху прямой y = b .
 Определение 1. e -окрестностью точки z0 называется
Определение 1. e -окрестностью точки z0 называется
множество точек z комплексной плоскости таких, что
| z - z0 |< e ,
где
e> 0 – заданное число.
 Условимся ее обозначить символом U e : U e ={z z - z
Условимся ее обозначить символом U e : U e ={z z - z
|
 < e}.
< e}.
z0 z0 0
|
0
точке
z0 (рис. 1.6).
8. Последовательности комплексных чисел

 Определение 2. Комплексное число a называется пределом последовательности
Определение 2. Комплексное число a называется пределом последовательности
комплексных чисел {z n}, если
"e > 0
$N = N(e),
"n > N
выполняется
zn - a < e.
Обозначают lim
n®¥
zn = a.
Последовательность, имеющая предел, называется
сходящейся.
Каждой последовательности комплексных чисел {z n}
соответствуют две
последовательности действительных чисел {x n}
Справедлива
и {yn}, где
z n = x n + iy n,
n =1,2,...
Теорема 1. Существование предела lim
n®¥
zn = a , где a = a + ib, равносильно
существованию двух пределов:
lim
n®¥
xn =a , lim
n®¥
yn = b.
Доказательство вытекает из определения предела и из неравенств



 Re z £
Re z £
z , Im z £ z ,
z1 + z2
£ z1 +
z2 .









 Из теоремы 1 следует, что сходящиеся последовательности комплексных чисел обладают такими же свойствами по отношению к арифметическим операциям, что и
Из теоремы 1 следует, что сходящиеся последовательности комплексных чисел обладают такими же свойствами по отношению к арифметическим операциям, что и
действительнозначные последовательности, например lim
n®¥
znzn =
lim
n®¥
zn ×
lim zn .
n®¥


 Если члены последовательности представлены в тригонометрической (экспоненциальной) форме, наряду с данной последовательностью можно рассмотреть последовательности модулей и аргументов её членов. Справедливы утверждения:
Если члены последовательности представлены в тригонометрической (экспоненциальной) форме, наряду с данной последовательностью можно рассмотреть последовательности модулей и аргументов её членов. Справедливы утверждения:
1. Если lim
n®¥
zn = a , то lim z n
 n®¥
n®¥
= a . (Очевидно из геометрических соображений).
2. Пусть
zn = r n eijn . Если lim jn = a, lim rn =r, то lim
z n = re ia . (Достаточное
n®¥
n®¥
n®¥
условие сходимости). Следует из формулы
z n = r n cosjn + ir nsin jn
и теоремы 1.
Заметим, что из сходимости последовательности комплексных чисел, вообще, не следует сходимость последовательности их аргументов.
 Определение 3. Последовательность {zn}
Определение 3. Последовательность {zn}
называется ограниченной, если
 $R, "n :
$R, "n :
zn < R.
9. Бесконечно удалённая точка
Понятие бесконечность или бесконечно удалённая точка вводится с помощью следующего определения:
Определение 4. Последовательность комплексных чисел {zn}
называется
сходящейся к бесконечности (или бесконечно большой последовательностью), т.е.

 если lim z n
если lim z n
n®¥
= +¥.
lim
n®¥
zn =¥,
Из этого определения следует
Определение 5. Множество точек комплексной плоскости, удовлетворяющее условию | z |= R > 0 , называют R-окрестностью бесконечно удаленной точки, и
обозначают
U R . Бесконечно удаленную точку обозначают символом ¥ , а
|
Согласно определению, бесконечно удалённая точка как бы «размазана» по всем направлениям и не имеет аргумента, как и точка z = 0.
Из свойств бесконечно больших комплекснозначных последовательностей по отношению к арифметическим операциям, которые аналогичны свойствам бесконечно больших действительнозначных последовательностей, вытекают свойства бесконечно удалённой точки:
z ± ¥ = ¥,
¥× z = ¥,
¥×¥ = ¥,
z = 0,

 ¥
¥
¥ = ¥,
 z
z
z = ¥ .
 0
0
Операции 0 ×¥ , ¥±¥, 0 , ¥


не имеют смысла. Для
0 ¥
|
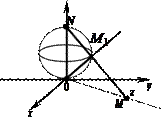
 получения геометрического изображения бесконечно удаленной точки z=∞, используют сферу радиуса 1 – сферу
получения геометрического изображения бесконечно удаленной точки z=∞, используют сферу радиуса 1 – сферу
Римана (рис.1.7). Каждая точка
M1 сферы – образ точки M
Рис 1.7
комплексной плоскости, которая является пересечением прямой
NM1 с
комплексной плоскостью, где N – верхний полюс сферы. При удалении M в
бесконечность по любому направлению, соответствующие точки
M1 на сфере будут
стремиться к N, т.е. точка N – изображение на сфере бесконечно удаленной точки комплексной плоскости z =¥. Наглядным представлением расширенной комплексной плоскости является вся сфера. Данное соответствие между точками комплексной плоскости и точками на сфере Римана называется стереографической проекцией. Комплексная плоскость, образованная лишь конечными точками, представляется сферой Римана, из которой исключена одна точка N.
Основная литература
1. И. В. Лавров, А. М. Терещенко. Теория функций комплексной переменной: Учеб. пособие / Министерство образования и науки РФ, Национальный исследовательский университет "МИЭТ". - 2-е изд. - М. : МИЭТ, 2015. - 168 с. - ISBN 978-5-7256-0788-8. 517.53(075.8) - Л-136 (стр. 5-21)
http://emirs.miet.ru/oroks- miet/upload/normal1/00s8qsquc0tc4v/Lavrov_Tereschenko_TFKP_2015.pdf
2. Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной [Текст]: Учебник для вузов / Под ред. А.Н. Тихонова, В.А. Ильина, А.Г. Свешникова. - 6-е изд., стер. - М. : Физматлит, 2010. - 336 с. - (Курс высшей математики и математической физики. Вып. 5). - ISBN 978-5-9221-0133-2. 517.53(075.8) - С-245
Дополнительная литература
1. И. Н. Бронштейн, К. А. Семендяев. Справочник по математике для инженеров и учащихся вузов [Электронный ресурс] : Учеб. пособие / - СПб. : Лань, 2010. - 608 с. - Доступ к электронной версии книги открыт на сайте http://e.lanbook.com/. - ISBN 978-5- 8114-0906-8. ЭБС Лань (стр. 466-470)
Видео-лекция от проекта «Лекторий» по теме «Комплексные числа» http://lectoriy.mipt.ru/lecture/Maths-ComplexAnalys-L01-Karlov-130904.03
Извлечения корня из компексных чисел
.

То есть k = 0, 1, 2, 3, . . ., n -1.
Матрицы


Рассмотрим виды квадратных матриц.

 Рассмотрим линейные операции над матрицами.
Рассмотрим линейные операции над матрицами.



Рассмотрим нелинейные операции над матрицами.







ОПРЕДЕЛИТЕЛИ





























Бинарные алгебраические операции
Пусть А– непустое множество элементов произвольной природы.
Определение . Бинарной алгебраической операцией на множестве А называется правило (закон), согласно которому каждой упорядоченной паре элементов a и b из А ставится в соответствие однозначно определенный элемент d из того же множества A. Элемент d называют композицией элементов a и b .
Обозначают:
d =  d = a § b d =
d = a § b d =  d =
d =  d = a + b d = a : b
d = a + b d = a : b
Примеры.
1.Сложение на множестве N={1, 2, 3, . . .} натуральных чисел является бинарной операцией, а вычитание не является бинарной операцией на множестве натуральных чисел. Действительно, разность (3 – 7) не является элементом множества N.
2.Вычитание на множестве Z={. . . -3, -2, -1, 0, 1, 2, 3, . . .} целых чисел является бинарной операцией, а деление не является бинарной операцией на множестве целых чисел. Действительно, разность (3 – 7) является элементом множества Z, а частное  не является элементом множества Z.
не является элементом множества Z.
3.Деление на множестве Q ={  } рациональных чисел не является бинарной операцией, так как не существует рационального числа, полученного в результате деления числа
} рациональных чисел не является бинарной операцией, так как не существует рационального числа, полученного в результате деления числа  на число 0. Если же число 0 удалить из множества Q , то деление будет бинарной операцией на множестве Q =
на число 0. Если же число 0 удалить из множества Q , то деление будет бинарной операцией на множестве Q = 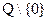 .
.
Определение . Бинарная операция  на множестве А называется коммутативной, если ("a , b ÎА) a
на множестве А называется коммутативной, если ("a , b ÎА) a  b = b
b = b  a .
a .
Определение . Бинарная операция  на множестве А называется ассоциативной, если ("a , b , с ÎА) (a
на множестве А называется ассоциативной, если ("a , b , с ÎА) (a  b)
b)  с = a
с = a  (b
(b  с) .
с) .
Определение . Бинарная операция  на множестве А называется дистрибутивной относительно операции
на множестве А называется дистрибутивной относительно операции  , если
, если
("a , b , с ÎА) a  (b
(b  с) = (a
с) = (a  b)
b)  (а
(а  с)
с)  (b
(b  с)
с)  a = (b
a = (b  a)
a) 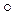 (с
(с  a) .
a) .
Примеры .
1). На множестве N натуральных чисел операции сложения и умножения коммутативны и ассоциативны, а операция умножения дистрибутивна относительно сложения:
("a, b, с Î N) a × (b + с)= a × b + a × с 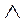 (b + с)× a= b × a + с × a ;
(b + с)× a= b × a + с × a ;
Операция сложения не дистрибутивна относительно умножения:
a + (b × с) 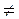 (a+ b) × (a+с) .
(a+ b) × (a+с) .
2). На множестве М квадратных матриц 3-го порядка операция сложения коммутативна и ассоциативна, а операция умножения ассоциативна, но не коммутативна; операция умножения дистрибутивна относительно сложения:
("a , b , с Î М) А× (В+ С) = А× В+ А× С 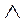 (В+ С) × А = В×А+ С× А .
(В+ С) × А = В×А+ С× А .
А× В 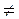 В×А
В×А
Определение . Элемент 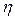 множества А называется нейтральным элементом относительно определенной на этом множестве бинарной алгебраической операции
множества А называется нейтральным элементом относительно определенной на этом множестве бинарной алгебраической операции  , если ("aÎА) a
, если ("aÎА) a 
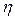 =
= 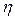
 a = a .
a = a .
 Замечание. Буква - «эта».
Замечание. Буква - «эта».
Примеры .
1.На множестве Z целых чисел число 0 является нейтральным элементом относительно сложения, а число 1 является нейтральным элементом относительно умножения.
2. На множестве N натуральных чисел число 1 является нейтральным элементом относительно умножения, а относительно сложения нет нейтрального элемента.
3. На множестве М квадратных матриц n -го порядка нулевая матрица является нейтральным элементом относительно сложения, а единичная матрица является нейтральным элементом относительно умножения.
Определение . Пусть в множестве А существует нейтральный элемент 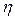 относительно определенной на этом множестве бинарной алгебраической операции
относительно определенной на этом множестве бинарной алгебраической операции  . Элемент
. Элемент 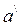 Î А называется симметричным элементу a Î А, если
Î А называется симметричным элементу a Î А, если  .
.
Примеры .
1.На множестве С комплексных чисел число -3+5 i является симметричным элементу 3 - 5 i относительно сложения, а число 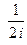 является симметричным элементу 2 i относительно умножения.
является симметричным элементу 2 i относительно умножения.
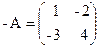
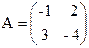
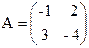 2. На множестве М квадратных матриц 2 -го порядка
2. На множестве М квадратных матриц 2 -го порядка

 , - симметричные элементы относительно сложения, а
, - симметричные элементы относительно сложения, а
, - симметричные элементы относительно умножения.
Задача . Найти нейтральный элемент множества действительных чисел R относительно операции  , которая определяется следующим образом:
, которая определяется следующим образом:
a  b = a + b +3
b = a + b +3
(где a, b - произвольные действительные числа).
Решение .
a 
 =
= 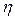
 a = a .
a = a .
a 
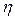 = a +
= a + 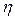 +3 = a;
+3 = a; 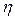
 a =
a = 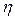 +a +3 = a .
+a +3 = a .
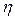 = -3 - нейтральный элемент.
= -3 - нейтральный элемент.
Для любого действительного числа a можем найти симметричный элемент относительно рассматриваемой операции:
 .
.
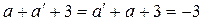 , откуда
, откуда 
Например, если a =7, то 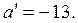
Группы

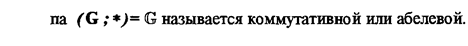

 Замечание.
Замечание.
- множество; - группа.



4). Множество N={1, 2, 3, . . .} натуральных чисел не образует группу
по сложению.

Задача . Проверить, образует ли группу множество действительных чисел относительно операции § , которая определяется следующим образом:
a § b =2 × (a + b)
(где a, b - произвольные действительные числа).
Решение . Операция § является бинарной алгебраической операцией на множестве R действительных чисел, так как ("a , b ÎR) 2 × (a + b) ÎR.
Проверим выполнимость аксиом группы:
а) ("a , b ,с ÎR) (a § b) §с = a §( b §с) – ложно, так как левая часть равна
(a § b) §с =(2 × (a + b))§с=2 × (2 × (a + b) + с ) = 4a +4 b +2 с, а правая часть равна a §( b §с) = a §(2 × (b+с))= =2 × ((a +2 × (b+с)) = 2a +4 b +4 с .
Поэтому операция § не ассоциативна. Выполнимость остальных аксиом группы далее можно не проверять.
Ответ: множество действительных чисел R не образует группу относительно операции §.
Кольца



Задача1 . Проверьте, образует ли кольцо множество
L = 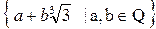 ?
?
Решение . Сложение является бинарной алгебраической операцией на множестве L, так как для любых  из множества L их сумма
из множества L их сумма
 .
.
Однако их произведение
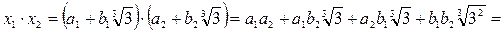
 ,
,
так как  - число не рациональное, т.е.
- число не рациональное, т.е. 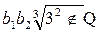 . Умножение не является бинарной алгебраической операцией на множестве L.
. Умножение не является бинарной алгебраической операцией на множестве L.
Ответ: множество L не образует кольца.
Задача2 . Проверьте, образует ли кольцо множество M матриц вида
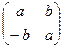 , где a,b
, где a,b  R ?
R ?
Решение . Сложение является бинарной алгебраической операцией на множестве M, так как для любых двух матриц из множества M их сумма принадлежит тому же множеству:
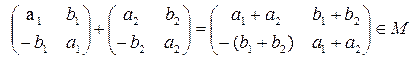 .
.
Умножение является бинарной алгебраической операцией на множестве M, так как для любых двух матриц из множества M их произведение принадлежит тому же множеству:
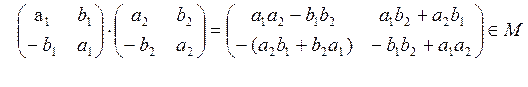 .
.
Проверим выполнимость аксиом кольца.
1.Выясним, образует ли множество M аддитивную абелеву группу:
а) ассоциативность сложения: А+(В+С) = (А+В)+С –истинно, так как это известно из свойств матриц, а M является подмножеством множества всех квадратных матриц 2-го порядка;
б) в множестве M существует нулевая матрица  , так как
, так как  ,
,
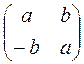 +
+  =
=  +
+ 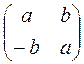 =
= 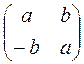 .
.
в) для любой матрицы А= 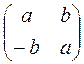 из множества M существует противоположная матрица
из множества M существует противоположная матрица
–А= 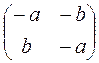 так, что выполняется (– А) +А=А+(– А) =О.
так, что выполняется (– А) +А=А+(– А) =О.
Из пунктов (а, б, в) следует, что множество M образует группу по сложению, то есть аддитивную группу;
г) эта группа абелева, так как сложение коммутативно:
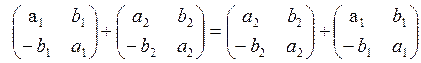 -известно из свойств матриц;
-известно из свойств матриц;
2. Умножение ассоциативно: А×(В×С) = (А×В)×С –истинно, так как это известно из свойств матриц, а M является подмножеством множества всех квадратных матриц 2-го порядка;
3. Умножение дистрибутивно относительно сложения:
(А+В)× С = А×С + С×В – правый дистрибутивный закон,
С×(А+В) = С×А+С×В – левый дистрибутивный закон. Они справедливы для любых квадратных матриц 2-го порядка и, в частности, для матриц множества M.
Из пунктов 1(а,б,в,г), 2, 3 следует, что множество M образует кольцо.
Поля

Задача1 . Проверьте, образует ли поле множество M матриц вида
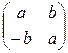 , где a,b
, где a,b  R ?
R ?
Решение. Ранее доказано, что множество M образует кольцо.
Проверим, является ли это кольцо полем.
4. а) несмотря на то, что на множестве всех квадратных матриц 2-го порядка А×В ¹ В×А, но для матриц рассматриваемого множества M

Видим, что для матриц рассматриваемого множества M
А×В = В×А -поэтому кольцо коммутативное;
б) выполняется операция деления, кроме деления на нулевую матрицу О:
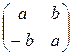 ×
×  =
=  имеет решение, если
имеет решение, если  , т.е.
, т.е. 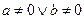 .
.
Действительно, 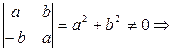 обратная матрица существует.
обратная матрица существует.
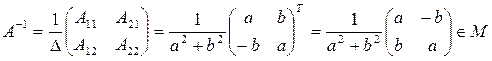 .
.
Тогда  =
=  ×
× 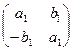 =
= 
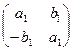 =
=
= 
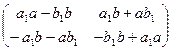
 .
.
Из п. а, б следует, что кольцо является полем.
Ответ: множество M матриц указанного вида образует поле.
Примечание. Вместо пункта б можно доказать, что существует единичная матрица
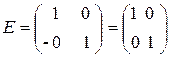
 такая, что Е × А = А× Е = А – для любой матрицы из множества M.
такая, что Е × А = А× Е = А – для любой матрицы из множества M.
Затем доказать существование обратной матрицы:
 A
A  M , A
M , A  0
0 
 A-1
A-1  M, т.к.
M, т.к.
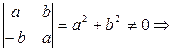 обратная матрица существует.
обратная матрица существует.
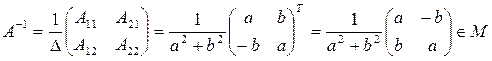 .
.
И тогда нет необходимости решать уравнение 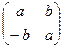 ×
× 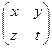 =
= 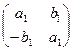 .
.
Дата добавления: 2021-02-10; просмотров: 122; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
