Парная линейная регрессия. Метод наименьших квадратов
Тема 2. Корреляционный и регрессионный анализ
Корреляция
В экспериментальных исследованиях одной из важных задач является анализ зависимостей между изучаемыми переменными. Зависимость может быть либо функциональной, либо стохастической (вероятностной). При функциональной зависимости величины 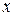 и
и 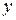 связаны точной математической формулой, например,
связаны точной математической формулой, например,  .
.
Для оценки тесноты и направления связи между изучаемыми переменными 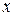 и
и 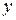 при их стохастической зависимости служит линейный коэффициент корреляции
при их стохастической зависимости служит линейный коэффициент корреляции  . Он характеризует степень тесноты не всякой, а только линейной зависимости. При нелинейной зависимости между явлениями применяют так называемое корреляционное отношение.
. Он характеризует степень тесноты не всякой, а только линейной зависимости. При нелинейной зависимости между явлениями применяют так называемое корреляционное отношение.
Пусть две случайные величины 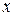 и
и 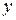 распределены по нормальному закону и имеется
распределены по нормальному закону и имеется  пар измеренных в опытах значений:
пар измеренных в опытах значений: 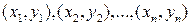 . О наличии связи между
. О наличии связи между 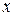 и
и 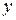 судят по выборочному парному коэффициенту корреляции
судят по выборочному парному коэффициенту корреляции  .
.
В теории разработаны несколько модификаций формул для расчета линейного коэффициента корреляции. Одна из формул:
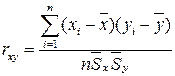 , (1)
, (1)
где 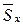 и
и 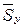 - среднеквадратичные отклонения соответственно для массивов (выборок)
- среднеквадратичные отклонения соответственно для массивов (выборок) 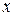 и
и 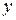 (в программе «Анализ данных» режим «Описательная статистика»
(в программе «Анализ данных» режим «Описательная статистика» 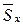 и
и 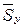 - стандартные отклонения);
- стандартные отклонения);
 ;
; 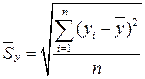 ,
,
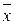 и
и  - средние значения соответственно в массивах
- средние значения соответственно в массивах 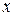 и
и 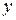 .
.
Величина  изменяется в пределах:
изменяется в пределах:  . Если
. Если  , то
, то 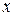 и
и 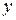 статистически независимы. Если
статистически независимы. Если  , то между
, то между 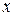 и
и 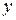 имеется идеальная функциональная зависимость, т.е. на графике
имеется идеальная функциональная зависимость, т.е. на графике 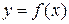 точки лежат на одной прямой линии (
точки лежат на одной прямой линии (  ).
).
|
|
|
В общем случае, когда величины 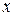 и
и 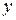 связаны произвольной вероятностной зависимостью,
связаны произвольной вероятностной зависимостью,  принимает значения в пределах
принимает значения в пределах  . Качественная оценка тесноты связи величин
. Качественная оценка тесноты связи величин 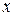 и
и 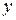 может быть выявлена на основании следующей шкалы:
может быть выявлена на основании следующей шкалы:
| Теснота связи | Значение | |
| прямой связи | обратной связи | |
| слабая | 0,1 – 0,3 | (-0,1) – (-0,3) |
| умеренная | 0,3 – 0,5 | (-0,3) – (-0,5) |
| заметная | 0,5 – 0,7 | (-0,5) – (-0,7) |
| высокая | 0,7 – 0,9 | (-0,7) – (-0,9) |
| весьма высокая | 0,9 – 0,99 | (-0,9) – (-0,99) |
Числовой пример. Имеются данные Госкомитета РФ за 1995 г (см. табл.).
| № п/п | Область | Уровень образования 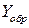
| Отношение числа безработных к числу вакансий
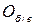
| Уровень преступности 
|
| 1 | Брянская | 735 | 22,3 | 908 |
| 2 | Владимирская | 788 | 10,8 | 792 |
| 3 | Ивановская | 779 | 52,9 | 804 |
| 4 | Калужская | 795 | 2,2 | 702 |
| 5 | Костромская | 740 | 10,4 | 685 |
| 6 | г. Москва | 902 | 0,4 | 496 |
| 7 | Московская | 838 | 2,4 | 536 |
| 8 | Нижегородская | 763 | 5,4 | 936 |
| 9 | Орловская | 762 | 4,1 | 662 |
| 10 | Рязанская | 757 | 4,1 | 671 |
| 11 | Смоленская | 772 | 1,0 | 920 |
| 12 | Тверская | 764 | 4,2 | 1040 |
| 13 | Тульская | 764 | 2,1 | 809 |
| 14 | Ярославская | 755 | 25,1 | 882 |
Уровень образования 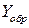 - это число лиц со среднеспециальным и высшим образованием на 1000 жителей.
- это число лиц со среднеспециальным и высшим образованием на 1000 жителей.
|
|
|
Уровень преступности  - это число преступлений на 100 000 жителей.
- это число преступлений на 100 000 жителей.
Результаты расчетов в виде таблицы коэффициентов парной корреляции  , вычисленных в программе «Анализ данных» режим «Корреляция» приведены в таблице.
, вычисленных в программе «Анализ данных» режим «Корреляция» приведены в таблице.
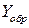
| 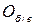
| 
| |
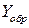
| 1 | ||
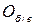
| -0,26 | 1 | |

| -0,66 | 0,24 | 1 |
Анализ расчетов:
- связь 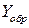 -
-  является заметной и обратной (
является заметной и обратной ( 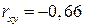 ), т.е. с возрастанием
), т.е. с возрастанием 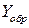
 уменьшается;
уменьшается;
- связь 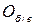 -
-  является слабой и прямой (
является слабой и прямой (  ), т.е. с увеличением
), т.е. с увеличением 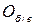 увеличивается
увеличивается  .
.
Поскольку выборочный коэффициент корреляции определен по ограниченной выборке, то необходимо проверить его значимость, т.е. установить достаточна ли величина  для обоснованного вывода о наличии корреляционной связи. Оценку значимости
для обоснованного вывода о наличии корреляционной связи. Оценку значимости  выполняют по величине
выполняют по величине 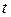 -критерия Стьюдента
-критерия Стьюдента
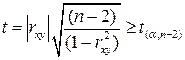 . (2)
. (2)
Здесь  - табличное значений
- табличное значений 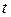 -распределения Стьюдента при уровне значимости
-распределения Стьюдента при уровне значимости 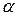 и числе степеней свободы
и числе степеней свободы  . Причем значение
. Причем значение  используется для двусторонней критической области.
используется для двусторонней критической области.
Если условие (2) выполняется, то считается, что между переменными 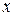 и
и 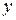 имеется статистически значимая корреляционная связь.
имеется статистически значимая корреляционная связь.
|
|
|
Для нашего примера: 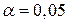 ;
; 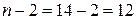 ;
;  .
.
Для переменных 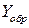 -
-  :
:
 .
.
Связь статистически значимая.
Для переменных 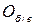 -
-  :
:
 .
.
Связь статистически не значимая.
В Excel коэффициент  определяет статистическая функция СТЬЮДРАСПОБР. Для нашего примера обращение к этой функции имеет вид =СТЬЮДРАСПОБР (0,05;12). Отметим, что эта функция дает значение
определяет статистическая функция СТЬЮДРАСПОБР. Для нашего примера обращение к этой функции имеет вид =СТЬЮДРАСПОБР (0,05;12). Отметим, что эта функция дает значение  для двусторонней критической области.
для двусторонней критической области.
Парная линейная регрессия. Метод наименьших квадратов
Пусть установлено наличие статистически значимой зависимости между физическими величинами 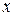 и
и 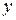 . Тогда эту зависимость можно аппроксимировать эмпирической формулой. Термин «аппроксимировать» имеет смысл «приближенно описать». Термины – «эмпирическая формула», «аппроксимирующая формула», «уравнение регрессии» имеют примерно одинаковое значение. Эмпирическая формула – это формула, полученная путем описания эмпирических (экспериментальных) данных.
. Тогда эту зависимость можно аппроксимировать эмпирической формулой. Термин «аппроксимировать» имеет смысл «приближенно описать». Термины – «эмпирическая формула», «аппроксимирующая формула», «уравнение регрессии» имеют примерно одинаковое значение. Эмпирическая формула – это формула, полученная путем описания эмпирических (экспериментальных) данных.
Результаты экспериментов представляют в виде таблицы:
Независимая переменная (фактор) 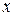
| 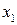
| 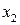
| 
| … | 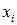
| … | 
|
Экспериментальные значения функции отклика 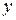
| 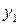
| 
| 
| … | 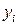
| … | 
|
Здесь  - объем выборки (число опытов),
- объем выборки (число опытов), 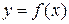 ; например,
; например, 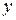 - продолжительность жизни человека (годы);
- продолжительность жизни человека (годы); 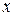 - количество выкуриваемых в день сигарет (штук). Другой пример:
- количество выкуриваемых в день сигарет (штук). Другой пример: 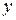 - предел прочности металла
- предел прочности металла  (МПа);
(МПа); 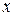 - температура нагрева металла (
- температура нагрева металла ( 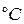 ).
).
|
|
|
Выбор вида формулы для описания зависимости 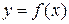 начинают с нанесения опытных значений
начинают с нанесения опытных значений 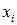 и
и 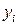 на график. Формула может быть линейной, квадратичной, степенной. Вид формулы подбирают по общему расположению опытных точек на графике. Пусть точки группируются около прямой линии. Тогда зависимость
на график. Формула может быть линейной, квадратичной, степенной. Вид формулы подбирают по общему расположению опытных точек на графике. Пусть точки группируются около прямой линии. Тогда зависимость 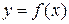 можно аппроксимировать линейным уравнением регрессии:
можно аппроксимировать линейным уравнением регрессии:
 , (1)
, (1)
где  - расчетные (по уравнению (1)) значения,
- расчетные (по уравнению (1)) значения,  и
и 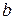 - коэффициенты регрессии. Новое обозначение «
- коэффициенты регрессии. Новое обозначение «  » указывает, что формула (1) отображает с некоторой вероятностью экспериментальную зависимость
» указывает, что формула (1) отображает с некоторой вероятностью экспериментальную зависимость 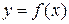 (
( 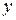 - исходные экспериментальные значения). Формула (1) является уравнением парной регрессии, так как
- исходные экспериментальные значения). Формула (1) является уравнением парной регрессии, так как 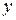 зависит от одного фактора
зависит от одного фактора 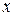 , т.е. рассматривается пара
, т.е. рассматривается пара 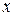 -
- 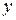 .
.
Коэффициенты  и
и 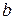 неизвестны и определяются по
неизвестны и определяются по  парам экспериментальных значений
парам экспериментальных значений  с помощью метода наименьших квадратов (МНК).
с помощью метода наименьших квадратов (МНК).
Суть МНК: коэффициенты регрессии  и
и 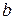 определяют из условия, что
определяют из условия, что
сумма квадратов отклонений (  )
)  опытных значений
опытных значений 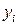 от рассчитанных по
от рассчитанных по
формуле (1)  должна быть минимальной:
должна быть минимальной:
 , (2)
, (2)
где  - остатки (отклонения; см. рис. 1). Здесь и далее
- остатки (отклонения; см. рис. 1). Здесь и далее 

Рис. 1. Графическая иллюстрация МНК
Для вычисления  и
и 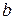 , минимизирующих
, минимизирующих  , необходимо вычислить частные производные функции
, необходимо вычислить частные производные функции  по аргументам
по аргументам  и
и 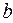 и приравнять их нулю:
и приравнять их нулю:
 ;
;  . (3)
. (3)
Подставим в (3)  из выражения (2) и вычислим производную по правилу дифференцируемой сложной функции:
из выражения (2) и вычислим производную по правилу дифференцируемой сложной функции:
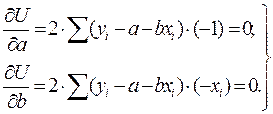 (4)
(4)
Преобразуем (4):
 (5)
(5)
Систему (5) принято называть системой нормальных уравнений. Решаем линейные системы уравнений (5) относительно неизвестных  и
и 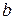 методом определителей (метод Крамера):
методом определителей (метод Крамера):
 ;
; 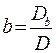 ,
,
где 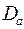 ,
,  ,
,  - определители;
- определители;
 ;
;
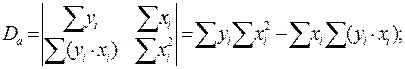
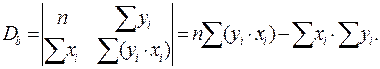
Пример. Имеются экспериментальные данные.
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 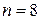
|
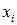
| 25 | 30 | 35 | 38 | 41 | 45 | 48 | 52 | |
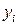
| 70 | 88 | 105 | 120 | 145 | 154 | 175 | 205 |
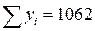 ;
;  ;
; 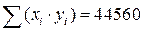 ;
; 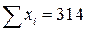 ;
;
 ;
;
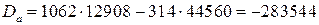 ;
;
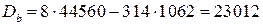 ;
;
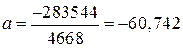 ;
;
 .
.
 .
.
Например:  .
.
Дата добавления: 2021-01-21; просмотров: 50; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
