Выделение полного квадрата в тригонометрических уравнениях.

Теория

Методы решения тригонометрических уравнений.

Разложение на множители.

2. Введение новой переменной:

а) сведение к квадратному;

б) универсальная подстановка;

в) введение вспомогательного аргумента.

Сведение к однородному уравнению.

Применение формул.

5. Использование свойств функций, входящих в уравнение:

а) обращение к условию равенства тригонометрических функций;

б) использование свойства ограниченности функции.

 

Уравнения, в которых все функции выражаются через одну тригонометрическую функцию от одного и того же аргумента.

Примеры: sin² x – cos x – 1 = 0,

                 tg 3x + 2 ctg 3x – 3 = 0.

Преобразованиями sin² x= 1 - cos² x и ctg 3x =  эти уравнения приводятся к алгебраическим, решая которые получаем простейшие тригонометрические уравнения. Метод сведения к квадратному состоит в том, что, пользуясь изученными формулами, надо преобразовать уравнение к такому виду, чтобы какую-то функцию (например, sin x или cos x) или комбинацию функций обозначить через y, получив при этом квадратное уравнение относительно y.

 

Уравнения, решаемые разложением на множители.

Под разложением на множители понимается представление данного выражения в виде произведения нескольких множителей. Если в одной части уравнения стоит несколько множителей, а в другой – 0, то каждый множитель приравнивается к нулю. Таким образом, данное уравнение можно представить в виде совокупности более простых уравнений.

Например: 

 sin 4x - cos 2x = 0,

2 sin 2x cos 2x - cos 2x = 0,

cos 2x (2 sin 2x – 1) = 0,

cos 2x = 0 или 2 sin 2x – 1 = 0.

 

3.Уравнения однородные относительно sin x и cos x .

Примеры: 3 sin² x + 4 sin x cos x + cos² x =0,

                  2 sin³ 5x - 2 sin² 5x cos 5x + sin 5x cos ²5x – cos³ x =0,

                        3 sin 7x - 2 cos 7x =0.

Если первый коэффициент не равен нулю, то разделив обе части уравнения на cosⁿ x, получим уравнение n - степени, относительно tg. Решая полученное уравнение перейдем к простейшему. При делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения cos x =0 корнями данного уравнения. Если cos x =0, то из уравнений следует, что sin x = 0. Однако sin x и cos x не могут одновременно равняться нулю, так как они связаны равенством sin² x + cos² x = 1. Следовательно, при делении уравнения на cosⁿ x, получаем уравнение, равносильное данному. В случае, если первый или последний коэффициент равен нулю, то имеет смысл вынести за скобки sin x или cos x. Решить уравнение приравняв к нулю каждый множитель.

 

Уравнения, сводящиеся к однородным.

Примеры:    3 sin² x - sin x cos x - 4cos² x =2,

                         sin³ x + sin x cos ²x – 2cos x =0.

Эти уравнения сводятся к однородным уравнениям следующим образом:

 

                         3 sin² x - sin x cos x - 4cos² x =2 (sin² x + cos² x),

                         sin³ x + sin x cos ²x – 2cos x(sin² x + cos² x) =0.

 

Уравнения, линейные относительно sin x и cos x

             а sin x + в cos x = с, где а, в и с – любые действительные числа.

Если а=в=0, а с 0, то уравнение теряет смысл;

Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество.

Рассмотрим случай, когда а,в,с 0.

Примеры:

                               sin x + 4 cos x = 1,

                             3 sin 5x - 4 cos 5x = 2,

                               2 sin 3x + 5 cos 3x = 8.

Последнее уравнение не имеет решений, так как левая часть его не превосходит 7.

Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tg ; сведением уравнения к однородному; введением вспомогательного аргумента и другими.

Рассмотрим последний из них.

Разделим обе части уравнения на .

Так как + = 1, то найдется аргумент φ, при котором

cos φ = , sin φ = .

Уравнение примет вид sin x cos φ + sin φ cos x = .

Используя формулу получим sin (x+ φ) = .

Следовательно решением уравнения будет х = (-1)ⁿ arcsin - arccos +pn, n Z.

Решение этого уравнения существует при a² + b²  c².

 

6.Уравнения, сводящиеся к равенству одной тригонометрической функции от различных аргументов:

 

1) sin x = sin у,         2) cos x = cos у,  3) tg x = tg у.

 

При решении этих уравнений можно применить метод использования условий равенства одноименных тригонометрических функций. Равенство этих функций имеет место тогда и только тогда, когда, соответственно, x = (-1)ⁿ y +pn,

x =  , x = y + .

 

sin f(x) = sin g(x) f(x) = g(x) + 2pk f(x) = p - g(x) + 2pn n Z, k Z

cos f(x) = cos g(x) f(x) = g(x) + 2pk f(x) = -g(x) + 2pn n Z, k Z

tg f(x) = tg g(x) f(x) = g(x) + pk g(x)  + pn n Z, k Z

     

Примеры:    cos 4x = sin 6х,    сtg x = tg .

Первое уравнение с помощью формул приведения приводим к виду :             sin( - 4x) = sin 6х, а второе – к виду tg ( - x) = tg .

Решим уравнение tg 3x tg (5x + 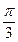) = 1.

Разделим обе части уравнения на tg 3x. Это допустимо, так как в данных условиях tg 3x не может равняться нулю:

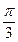 tg (5x + ) = , tg (5x + 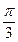) = сtg 3x, tg (5x + 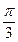) = tg (  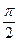- 3x).

На основании условия равенства тангенсов двух углов имеем:

5x + 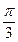-  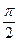+ 3x = pn;

8х =  + pn; х = + ; х = (6n + 1) , n Z.

При каждом значении х из этой совокупности каждая из частей уравнения tg (5x + 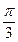) = tg (  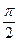- 3x) существует.

Уравнения sin x = sin у и cos x = cos у можно решать и с применением формул, заменив разность функций произведением.

 

Выделение полного квадрата в тригонометрических уравнениях.

Примеры:

                            

                     sin⁴ x + cos⁴ x = sin 2х,

                      cos⁶ x + sin⁶ х = cos 2x,

     cos⁶ x + sin⁶ х + sin⁴ x + cos⁴ x = 1 - sin 2х.

Данный метод можно применить для уравнений, содержащих следующие выражения:

                sin⁴ x + cos⁴ x, cos⁶ x   sin⁶ х, sin⁸ х  cos⁸ x.

Преобразуем первое выражение:

  

sin⁴ x + cos⁴ x = sin⁴ x + 2 sin² x cos ²x +cos⁴ x - 2 sin² x cos ²x = (sin² x + cos ²x)² - 2 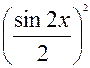= 1 -  sin² 2х .

Преобразуем второе выражение:

 cos⁶ x + sin⁶ х = (cos² x + sin² х) ( sin⁴ x - sin² x cos ²x +cos⁴ x) = 1 -  sin² 2х -  sin² 2х = 1 -  sin² 2х.

cos⁶ x - sin⁶ х = (cos² x - sin² х) ( sin⁴ x + sin² x cos ²x +cos⁴ x) = cos 2x (1 -  sin² 2х +  sin² 2х) = cos 2x (1 -  sin² 2х).

Можно упростить эти выражения и с помощью формул понижения степени.

 

8. Уравнения вида f( sin х + cos x , sin х cosx ) = 0, f( sin х - cos x , sin х cosx ) = 0.

Решить такие уравнения можно заменой sin х + cos x = t или sin х - cos x = t.

Примеры: 

                  sin х + cos x = 1 + sin 2х,

                  6 sinх cosx + 2 sin х = 2 + 2 cos x,

                  3 sin 3х = 1 + 3 cos 3x - sin 6х.

После преобразования и соответствующей замены эти уравнения сводятся к квадратным. В первом уравнении, сделав замену sin х + cos x = t, получим

sin² x + 2 sin x cos x +cos² x = t², 1 + sin 2х = t², sin 2х = 1 - t². Уравнение примет вид t = 1 + 1 - t².

Задание: Решить уравнения

1. sinx = 0;

2. 2tg3x = 0;

3. 2cosx = 1;                                 

4. 2sin(2x – 4π) = ;                  

5. cos²2x = 2;

6. 1 – sin²x = 0;

7.  2cos²x -5cosx – 3 = 0;                           

8. 3sin²x + 7cosx – 3 = 0;

9. 2tg²3x – 3tg3x + 1 = 0;          

---

Дата добавления: 2020-12-12; просмотров: 160; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!