Пример расчета полосового фильтра.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Произвести расчет ПФ при следующих исходных параметрах: w_н= 0.3p, w_в= 0.6p, D_p = 0.1p, d = 0.02.

1. А = -20 log d. А = 34.

2. N = p (A-7.95)/(14.36 D_p). N = 18.

3. b = 0.5842(A-21)^0.4 +0.07886(A-21). b = 2.62.

4. h_о = (w_в-w_н)/p. h_о = 0.3

5. h(n) = (sin nw_в-sin nw_н)/(np). h(n)= 0.04521, -0.24490, -0.09515, ... , 0.02721.

6. p_n= J_o{b } / J_o{b}. p_n= 1.00, 0.997, 0.9882, .......

7. Оператор фильтра: h_n = p_n h(n), n = 0, 1, 2,..., N. h_-_n = h_n. h_n = 0.3000, 0.04508, -0.2420, ....

8. Проверка по формуле: H(w) = h_n cos nw, 0 £ w £ p.

Для оценки формы передаточной функции количество точек спектра в интервале 0-p достаточно задать равным 2N, т.е. с шагом Dw £ p/36.

Влияние конечной разрядности на цифровые фильтры должно быть минимальным и не создавать на их частотных характеристиках дополнительных неравномерностей и отклонения от заданной формы. С чисто практической точки зрения ограничение разрядности коэффициентов фильтра в целях повышения производительности вычислений лучше всего (и проще всего) выполнять непосредственно сравнением частотных характеристик с изменением разрядности от большей к меньшей. Следует учитывать, что ограничение разрядности может по разному сказываться на неравномерности фильтра в полосе пропускания и степени затухания сигналов в полосе подавления.

Ошибки отклонения e(w) частотной характеристики относительно заданной при проектировании кроме разрядности коэффициентов В в битах зависит также от размеров N оператора фильтра и в первом приближении может оцениваться по формулам:

|e(w)| = N 2^-B, (7.3.4)

|e(w)| = 2^-B(N/3)^1/2, (7.3.5)

|e(w)| = N 2^-B[(N ln N)/3]^1/2. (7.3.6)

Выражение (7.3.4) наиболее пессимистично и предполагает наихудшие ситуации вычислений. Два других выражения носят более реальный характер по статистическим данным.

Курсовая работа 8-07. Разработка программы расчета универсального частотного НЦФ (низкочастотный, высокочастотный, полосовой) и его использования при обработке цифровых сигналов.

Гладкие частотные фильтры /24/.

В некоторых случаях (при последовательном соединении фильтров, при выделении сигналов на уровне сильных помех и т.п.) осцилляции на передаточных характеристиках фильтров являются весьма нежелательными даже при их малой остаточной величине. Так, например, двойное последовательное применение фильтров приводит к тому, что ошибки в полосе пропускания приблизительно удваиваются, а полосе подавления возводятся в квадрат, при этом длина окна эквивалентного фильтра практически удваивается.

Принцип синтеза фильтров. Очевидно, что фильтры с гладкой передаточной характеристикой можно получить только в том случае, если возможно разложение передаточной функции в конечный ряд Фурье.

Допустим, мы имеем симметричный НЦФ с передаточной функцией:

H(w) = h_о+2 h_ncos nw. (7.4.1)

Как известно, cos nw равен полиному по cos w степени n, при этом выражение (7.4.1) можно записать в виде:

H(w) = g_n (cos w)ⁿ = g_nxⁿ, (7.4.2)

где переменная х=cos w изменяется от 1 до -1 (поскольку w изменяется от 0 до p). Преобразование переменной представляет собой нелинейное растяжение оси абсцисс с поворотом на 180^o (по переменной х передаточные функции ФНЧ похожи на ФВЧ, и наоборот) с выражением функции через степенной полином. Последнее примечательно тем, что синтез гладких функций на базе степенных полиномов затруднений не представляет.

Так, например, для конструирования ФНЧ в качестве исходной может быть принята степенная функция вида:

g(x)= (1+x)^z(1-x)^r, (7.4.3)

где z и r - параметры.

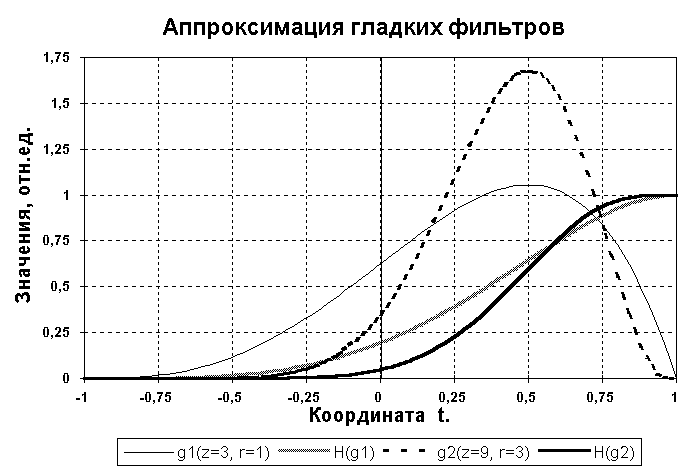
Рис. 7.4.1. Примеры синтеза гладких фильтров.

Функция (7.4.3) имеет нули порядка z и r в точках соответственно х = -1 и х = 1 (рис. 7.4.1), при этом значения параметров z и r характеризуют степень касания функцией оси абсцисс. Чем больше порядок, тем медленнее функция отходит ("отрывается") от оси абсцисс.

Если выражение функции (7.4.3) проинтегрировать в пределах от -1 до х и нормировать на значение интеграла от -1 до 1 , то будет получена гладкая передаточная характеристика низкочастотного фильтра. На рисунке 7.4.1 приведены передаточные функции для двух пар параметров z и r, вычисленные по формуле:

H(x)= g(x)dx / g(x)dx. (7.4.4)

Рис. 7.4.2. Схема возврата к ряду Фурье.

Функция H(x) имеет перегиб в точке (z-r)/(z+r) и переходную зону, крутизна которой тем больше, чем больше значения z и r. Подстановкой x=cos w осуществляется возврат к частотной переменной w с сохранением монотонности функции.

В заключение, для определения коэффициентов фильтра h_n требуется осуществить обратное преобразование от степенной формы (7.4.2) к ряду Фурье (7.4.1). Выполнение данной операции достаточно просто производится рекурсивным способом, показанным на рис. 7.4.2. Подробное обоснование рекурсии приведено в /24/.

Дата добавления: 2021-01-21; просмотров: 55; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 Следующая ⇒

Мы поможем в написании ваших работ!