Сущность понятия. Содержание и объем понятия. Соотношение между содержанием и объемом

Понятие – форма мышления, в которой отражены существенные свойства (признаки) объектов изучения.

При использовании понятий в конкретной обстановке мы пользуемся дедуктивным путем мышления (от общего к частному), который ввел Аристотель.

Введем обозначения:

Х – множество объектов,

А – понятие,

а – признак понятия.

Признак а называется основным или необходимым, существенным признаком понятия А, если все объекты множества Х обладают этим признаком (свойством).

Признак а называется отделимым признаком понятия А, если некоторые объекты множества Х обладают этим признаком.

Признак а называется противоречивым признаком понятия А, если ни один объект множества Х не обладает этим признаком.

Понятия обозначают заглавными буквами латинского алфавита, затем ставится двоеточие и в кавычках пишется само понятие.

Пример. А: «параллелограмм».

Основной признак – параллельность противоположных сторон параллелограмма.

Отделимый признак – перпендикулярность диагоналей параллелограмма.

Противоречивый признак – только две стороны параллелограмма параллельны.

Объемом понятия называют множество объектов, на которые распространяется данное понятие.

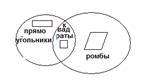
Например, понятием «параллелограмм» охватываются и прямоугольники, и ромбы, и квадраты, и параллелограммы, которые ими не являются.

Содержание понятия – это совокупность основных признаков, которые охватываются этим понятием.

Содержание раскрывается в определении. Чем «уже» объем понятия, тем «шире» его содержание и наоборот.

Родовые и видовые понятия

Более общее – родовое понятие, менее общее – видовое понятие.

Если все основные признаки понятия А являются основными для понятия В, но не все основные признаки понятия В являются основными для понятия А, то понятие А называется родовым, а понятие В – видовым.

Например, в определении «параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны» параллелограмм – видовое понятие, а четырехугольник – родовое понятие.

Отношение между понятиями

Понятия

Сравнимые Несравнимые

Совместимые Несовместимые

Отношение Отношение Отношение

равнозначности частичного полного

совпадения подчинения

Сравнимые понятия те, которые имеют общие признаки.

Совместимые понятия те, которые частично или полностью совпадают. Например, ромб и прямоугольник.

Отношение равнозначности имеет место тогда, когда объемы понятий полностью совпадают. Например, множество целых положительных чисел совпадает с множеством натуральных чисел.

Отношение частичного совпадения имеет место тогда, когда объемы понятий пересекаются. Например, понятия «прямоугольник» и «ромб».

Отношение полного подчинения имеет место тогда, когда объем одного понятия является правильной частью объема другого понятия. Например, понятия «параллелограмм» и «ромб».

Определение понятий

Определением называют такую логическую операцию, при помощи которой раскрывается содержание понятия через перечисление существенных признаков.

Существенные признаки – это такие признаки, каждый из которых является основным, а вместе независимыми и достаточными для того, чтобы отличить объекты данного рода от других объектов.

Виды определений: явные и неявные.

Явные определения имеют форму равенства, совпадения двух понятий.

Например, «параллелограмм – это четырехугольник, …». Схема определения: «А – это В», где А и В - понятия.

Неявные определения не имеют формы совпадения двух понятий.

Примеры таких определений:

· контекстуальные (через фрагмент текста);

· остенсивные (с помощью показа объектов);

· генетические (показан способ образования объекта);

· индуктивные (указаны некоторые объекты и правила получения следующего).

В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через анализ конкретной ситуации, описывающий смысл вводимого понятия. Например, определение уравнения в учебниках математики.

Остенсивные определения используются для введения терминов путем демонстрации объектов, которые этими терминами обозначаются. Поэтому остенсивные определения еще называют определениями путем показа (понятия равенства и неравенства в начальной школе).

В генетических определениях указывается способ образования определенного объекта. Например, шар, это геометрическая фигура, полученная в результате вращения полукруга вокруг диаметра.

В индуктивных определениях указываются некоторые объекты теории и правила, позволяющие получать новые из уже имеющихся. Например, арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

Чаще всего в математике используют определения через род и видовое отличие.

Структура определения:

1) Указывается род или родовое понятие, которому принадлежит данное понятие как вид.

2) Указываются те признаки, которые отличают данный вид от других видов данного рода.

_{видовое, определяемое понятие родовое, определяющее понятие видовой признак}

Пример. Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Определение состоит из двух частей: определяемого и определяющего понятий.

То понятие, которое определяется, называется определяемым. Определяющее понятие то, через которое определяется данное понятие.

Требования к определениям

1) Соразмерность определяемого и определяющего понятий.

2) В определении не должно быть порочного круга.

3) В определении должны быть указаны все свойства, однозначно определяющие объекты, принадлежащие объему определяемого понятия.

4) Отсутствие в определении избыточности.

Определение, которое удовлетворяет перечисленным требованиям, называется корректным.

Нарушения:

1) Параллелограмм - это многоугольник, у которого противоположные стороны попарно параллельны. Этому определению удовлетворяют шестиугольники, восьмиугольники и т.д.

2) Прямым углом называются угол, который образован перпендикулярными прямыми. Перпендикулярные прямые – это прямые, образующие прямой угол. Определение прямого угла дается через определение перпендикулярных прямых, а те, в свою очередь, определяются через прямой угол, т.е. получился порочный круг.

3) 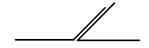Смежными называются углы, которые в сумме дают 180°. Возможна следующая комбинация углов:

А это не смежные углы.

4) Прямоугольником называется четырехугольник, у которого противоположные стороны равны и параллельны. Здесь указано лишнее свойство, которое вытекает из первого свойства.

4.1.3. Математические предложения

Общие теоретические сведения

Понятие логики.

Логика – наука о законах мышления. Формальная логика – наука об элементарных законах и формах правильного мышления.

Математическая логика – исходит из основных законов формальной логики, использует логические процессы с помощью математических методов, полное отвлечение от конкретного содержания предложения.

Пример. Если все растения – красные, а все собаки – растения, то все собаки красные. С точки зрения формальной логики - это полная ерунда, а с точки зрения математической логики предложение составлено абсолютно верно.

Понятие высказывания.

Основным объектом исследования математической логики является высказывание.

Рассмотрим предложения:

1) Город Тверь стоит на Волге.

2) Солнце больше Земли.

3) 13 – четное число.

4) Сегодня - вторник.

5) Существуют прямоугольные треугольники.

Все это утвердительные повествовательные предложения, верные или неверные.

Высказывание (простое высказывание) – это утвердительное повествовательное предложение, которое может быть истинным или ложным.

В математической логике высказывания обозначаются заглавными буквами латинского алфавита: A, B, C, …

В начальной школе вместо слова «высказывание» используют специальные значки: >, <, = .

Высказывания бывают истинными и ложными. В примерах высказывания 1, 2, 5 – истинные, а высказывания 3, 4 – ложные. Кроме этого высказывания бывают простыми и составными (сложными).

Простым или элементарным высказыванием называют такие высказывания, которые нельзя расчленить на другие высказывания. Если высказывание допускает расчленение на другие высказывания, то его называют составным.

Сложное высказывание состоит из ряда связанных простых высказываний. При этом используются слова-связки: «неверно, что», «не», «и», «или», «если…, то…», «тогда и только тогда, когда». Каждой логической связке сложного высказывания соответствует логическая операция, имеющая свое символьное обозначение (см. табл. 1).

Таблица 1

Условные обозначения логических связок

Связка	Операция	Обозначение	Правила чтения	Пример А – Преподаватель читает лекции, В – Преподаватель ведет практику
Не	Отрицание		Не А	- Преподаватель не читает лекции, - Преподаватель не ведет практику
И	Конъюнкция	А ∧ В	А и В	А ∧ В – Преподаватель читает лекции и (преподаватель) ведет практику
Или	Дизъюнкция	А ∨ В	А или В	А ∨ В – Преподаватель читает лекции или (преподаватель) ведет практику
Если…, то…	Импликация	А⇒ В	Если А, то В	А⇒ В – Если преподаватель читает лекции, то он (преподаватель) ведет практику
…, тогда и только тогда, когда…	Эквиваленция	А⇔ В	А тогда и только тогда, когда В	А⇔ В – Преподаватель читает лекции, тогда и только тогда, когда он (преподаватель) ведет практику

Истинное высказывание условимся обозначать латинской буквой T (true), ложное высказывание F (false).

Операции над высказываниями

Отрицание высказывания

Пример. Дано высказывание А: «2 + 1 = 3» - истинно. Составим высказывание вида «Неверно, что А»: «неверно, что 2 + 1 = 3» - оно ложно. Последнее высказывание можно сформулировать и так «Не А»: «2 + 1 ≠ 3» - ложь. Полученные высказывания называют отрицанием высказывания А и обозначают .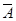

Определение. Высказывание вида 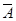(«неверно, что А», «не А») называется отрицанием высказыва - ния А. Отрицание ложно, если само высказывание А - истинно, отрицание истинно, если высказывание А ложно.

Вторую часть определения отрицания высказывания можно оформить в таблице истинности.

Таблица истинности.

А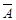
и	л
л	и

Закон двойного отрицания: = А

Для доказательства составляем таблицу истинности и заполняем ее. Сравнивая по строчкам значения первого и последнего столбиков делаем вывод о том, что закон доказан

Конъюнкция высказываний

Пример. Рассмотрим высказывания А: «2 + 1 = 4» - ложно, В: «15 кратно 5» - истинно. Составим высказывание вида «А и В»: «2 + 1 = 4 и 15 кратно 5» - оно ложно. Полученное высказывание называют конъюнкцией высказываний А и В и обозначают А ∧ В.

Определение. Высказывание вида А ∧ В («А и В») называется конъюнкцией высказываний А и В. Конъюнкция высказываний истинна, если оба высказывания истинны, в остальных случаях конъюнкция ложна.

Вторую часть определения отрицания высказывания можно оформить в таблице истинности.

Таблица истинности.

А	В	А ∧ В
и	и	и
и	л	л
л	и	л
л	л	л

Законы конъюнкции:

1) А ∧ А = А

2) А ∧ В = В ∧ А – коммутативность или переместительный закон

3) (А ∧ В) ∧ С = А ∧ (В ∧ С) – ассоциативность или сочетательный закон

4) А ∧ 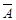= «л»

Для доказательства составляем таблицу истинности и заполняем ее. Сравнивая по строчкам значения первого и последнего столбиков делаем вывод о том, что закон доказан.

А		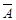А ∧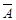
и	л	л
л	и	л

Докажем четвертый закон.

Дизъюнкция высказываний

Пример. Рассмотрим высказывания А: «2 + 1 = 4» - ложно, В: «15 кратно 5» - истинно. Составим высказывание вида «А или В»: «2 + 1 = 4 или 15 кратно 5» - оно истинно. Полученное высказывание называют дизъюнкцией высказываний А и В и обозначают А ∨ В.

Определение. Высказывание вида А ∨ В («А или В») называется дизъюнкцией высказываний А и В. Дизъюнкция высказываний ложна, если оба высказывания ложны, в остальных случаях дизъюнкция истинна.

Вторую часть определения отрицания высказывания можно оформить в таблице истинности.

Таблица истинности.

А	В	А ∨ В
и	и	и
и	л	и
л	и	и
л	л	л

Законы дизъюнкции:

1) А ∨ А = А

2) А ∨ В = В ∨ А – коммутативность или переместительный закон

3) (А ∨ В) ∨ С = А ∨ (В ∨ С) – ассоциативность или сочетательный закон

4) А ∨ 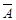= «и»

А	В	А ∨ В	В ∨ А
и	и	и	и
и	л	и	и
л	и	и	и
л	л	л	л

Докажем второй закон.

Импликация высказываний

Пример. Рассмотрим высказывания А: «2 + 1 = 4» - ложно, В: «15 кратно 5» - истинно. Составим высказывание вида «Если А, то В»: «если 2 + 1 = 4, то 15 кратно 5» - оно истинно. Полученное высказывание называют импликацией высказываний А и В и обозначают А ⇒ В.

Определение. Высказывание вида А ⇒ В («если А, то В» или «из А следует В») называется импликацией высказываний А и В. Импликация высказываний А и В ложна, если первое высказывание А – истинно, а второе высказывание В - ложно, в остальных случаях импликация истинна. Высказывание А называют условием импликации, а высказывание В – заключением.

Вторую часть определения отрицания высказывания можно оформить в таблице истинности.

Таблица истинности.

А	В	А ⇒ В
и	и	и
и	л	л
л	и	и
л	л	и

Виды импликации:

1) Данная импликация А ⇒В: «если 2 + 1 = 4, то 15 кратно 5» - истинна.

2) Обратная импликация (меняем местами условие и заключение данной импликации) В⇒А: «если 15 кратно 5, то 2 + 1 = 4» - ложна.

3) Противоположная импликация (в данной импликации условие и заключение заменяем их отрицаниями) 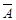⇒ : «если 2 + 1 ≠ 4, то 15 не кратно 5» - истинна.

4) Обратная противоположной (в обратной импликации условие и заключение заменяем их отрицаниями) или противоположная обратной (в противоположной импликации меняем местами условие и заключение) ⇒ 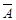: «если 15 не кратно 5, то 2 + 1 ≠ 4» - ложна.

Вывод: одновременно истинны или ложны данная импликация и обратная противоположной, а также обратная и противоположная.

Эквиваленция высказываний

Пример. Рассмотрим высказывания А: «2 + 1 = 4» - ложно, В: «15 кратно 5» - истинно. Составим высказывание вида «А тогда и только тогда, когда В»: «2 + 1 = 4 тогда и только тогда, когда 15 кратно 5» - оно ложно. Полученное высказывание называют эквиваленцией высказываний А и В и обозначают

А ⇔ В.

Определение. Высказывание вида А ⇔В («А тогда и только тогда, когда В») называется эквиваленцией высказываний А и В. Эквиваленция высказываний А и В истинна, если оба высказывания одновременно истинны или одновременно ложны, в остальных случаях эквиваленция ложна.

Вторую часть определения отрицания высказывания можно оформить в таблице истинности.

Таблица истинности.

А	В	А ⇔ В
и	и	и
и	л	л
л	и	л
л	л	и

Другие законы операций над высказываниями:

Дистрибутивные законы, связывающие конъюнкцию и дизъюнкцию

(А ∨ В) ∧ С = (А∧ С) ∨ (В ∧ С)

(А ∧ В) ∨ С = (А∨ С) ∧ (В ∨ С)

Формулы, имеющие все значения истинности при любых значениях переменных, называются тождественно-истинными. Тождественно-истинные формулы являются законами логики.

Логические законы доказываются с помощью таблиц истинности.

Алгоритм перевода высказываний с естественного языка на формальный

1. Выделить и обозначить простые высказывания.

2. Найти логические связки и заменить их на соответствующие логические операции.

3. Записать логическую формулу сложного высказывания.

4. Сделать проверку на соответствие полученной формулы исходному высказыванию.

Алгоритм перевода высказывания с формального языка на естественный

1. Заменить логическую переменную простым высказыванием.

2. Логические операции заменить соответствующими логическими связками.

3. Составить предложение.

Используя перевод естественной речи на язык математической логики, таблицы истинности, законы формальной логики в рассуждениях, а также теорию графов, можно решать текстовые задачи, встречающиеся в повседневной и профессиональной деятельности любого человека.

Дата добавления: 2021-01-21; просмотров: 577; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 Следующая ⇒

Мы поможем в написании ваших работ!