Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
Билет.
1) I. Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны.
II. Если две параллельные прямые пересечены секущей, то сумма внутренних односторонних углов равна 180°.
III. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
2) Треуго́льник — это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Если все углы треугольника острые, то треугольник называется остроугольным;
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Если сумма углов треугольника равна 180о, то такой треугольник называется развернутым.
§ Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
§ Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
|
|
|
§
§ Формулировка теоремы косинусов:
§
§ Для плоского треугольника со сторонами a,b,c и углом α, противолежащим стороне a, справедливо соотношение:
§ 
§ квадрат одной стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного их произведения, умноженного на косинус угла между ними.
§
§ Доказательство теоремы косинусов:
§
§ 
§ Рассмотрим треугольник ABC.
Из вершины C на сторону AB опустим высоту CD.
§ Исходя из того, что треугольник ADC является прямоугольным, то величину стороны AD можно найти из соотношения тригонометрических функций :
AD / AC = cos α
AD = AC cos α
AD = b cos α
§ Длину стороны BD найдем как разность AB и AD:
BD = AB - AD
BD = c − b cosα
Теперь запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
CD2 + BD2 = BC2
CD2 + AD2 = AC2
откуда
CD2 = BC2 - BD2
CD2 = AC2 - AD2
§ Поскольку левые части уравнений равны, то приравняем правые части уравнений:
BC2 - BD2 = AC2 - AD2
§ подставим значения сторон (a,b,c)
a2 - ( c − b cos α )2 = b2 - ( b cos α )2
a2 = ( c − b cos α )2 + b2 - ( b cos α )2
a2 = b2 + c 2 - 2bc cos α + ( b cos α )2 - ( b cos α )2
a2 = b2 + c 2 - 2bc cos α
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
|
|
|
Второй способ решения задачи. Координатный метод.
| 1. Введём прямоугольную систему координат с началом в точке А так, чтобы точка В лежала на положительной полуоси AX, а точка С имела положительную ординату. Решение записывают все учащиеся. | |
| 2. Запишем координаты точек: B(c; 0) ; C(bcosA; bsinA). 3. Найдём квадрат стороны BC: BC2 = a2 = (bcosA - c)2 + (bsinA)2 = = b2cos2A – 2bccosA + c2 + b2sin2A = = b2(cos2A + sin2A) + c2 – 2bccosA = = b2 + c2 – 2bccosA. a2 = b2 + c2 – 2bccosA – теорема косинусов b2 = a2 + c2 – 2accosB c2 = b2 + a2 – 2abcosC | 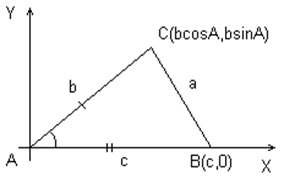 Рис. 5 Рис. 5
|
Вывод: Таким образом, квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
Следствия теоремы косинусов!
1. Если c^2=a^2+b^2 значит треугольник прямоугольный
2. Если с^2 меньше a^2+b^2 то угол острый. Если С наибольшая сторона, то треугольник остроугольный
3. Если c^2 больше a^2+b^2 то угол тупой
4. В треугольнике против большей стороны лежит больший угол, против большего угла лежит большая сторона.
p.S. Под углом понимается угол между а и в
Знак ^ - знак степени
2 билет.
1) Два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные.
|
|
|
Свойство: Вертикальные углы равны.
Теорема о вертикальных углах.
Если две прямые пересекаются в точке, образуются четыре угла. Несмежные углы называютсявертикальными или противоположно вертикальными углами. Также, каждая пара прилегающих углов образует прямую, а эти углы называются смежными[1]. Поскольку каждая пара вертикальных углов является смежными к прилегающим, то градусные меры вертикальных углов — равны.
2) Треуго́льник — это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Если все углы треугольника острые, то треугольник называется остроугольным;
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Если сумма углов треугольника равна 180о, то такой треугольник называется развернутым.
|
|
|
§ Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
§ Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Теорема Синусов.
Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство.
Пусть есть Δ ABC со сторонами a, b, с и углами α, β, γ.
Докажем, что

Проведем из точки С высоту CD. Тогда из Δ ACD получим:

Если угол α тупой, то

Из Δ BCD получаем
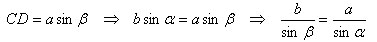
Аналогично получаем
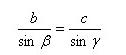
Теорема доказана.
Следствие
Для треугольника АВС с радиусом описанного круга R выполнены соотношения:
 .
.
3 билет.
1) Два угла, у которых одна сторона общая, а две другие являются продолжениями другой, называются смежными.
Следствия
1. Если два угла равны, то смежные с ними углы равны.
2. Если смежные углы равны, то они прямые.
3. Угол, смежный с прямым углом, прямой.
4. Угол, смежный с тупым углом, острый.
5. Угол, смежный с острым углом, тупой.
6. Если угол неразвернутый, то его градусная мера меньше 180°.
2) Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов).
Теорема Пифагора
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a + c.
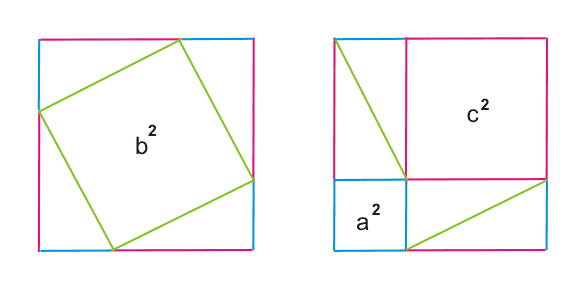
В одном случае (слева) квадрат разбит на квадрат со стороной b и четыре прямоугольных треугольника с катетами a и c.
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
4 билет.
1) Треуго́льник — это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти три точки.
Если все углы треугольника острые, то треугольник называется остроугольным;
Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
Если сумма углов треугольника равна 180о, то такой треугольник называется развернутым.
§ Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
§ Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
§ Два треугольника называются равными ( Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны
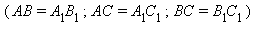
|
§
и соответствующие углы равны

|
§
2. Равные треугольники совпадают при наложении
Признаки равенства:
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
2)
Теорема Фалеса
Теорема.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство.
Пусть точки A1, A2, A3 – точки пересечения параллельных прямых с одной из сторон угла. А точки B1, B2, B3 – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A1A2 = A2A3, то B1B2=B2B3.
Проведем через точку В2 прямую С1С2, параллельную прямой A1A2. Получаем параллелограммы A1C1BA2 и A2B2C2A3. По свойствам параллелограмма, A1A2 = C1B2 и A2A3 = B2C2. Так как A1A2 = A2A3, то C1B2 = B2C2.
Δ C1B2B1 = Δ C2B2B3 по второму признаку равенства треугольников (C1B2 = B2C2, ∠ C1B2B1 = ∠ C2B2B3, как вертикальные, ∠ B1C1B2 = ∠ = B3C2B2, как внутренние накрест лежащие при прямых B1C1 и C2B3 и секущей С1С2). Из равенства треугольников следует, что B1B2=B2B3. Теорема доказана.
5 билет.
1) Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

Признаки.
1) Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
2) Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
3) Если в четырехугольнике противолежащие углы равны, такой четырехугольник – параллелограмм.
1) Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема о центре окружности, описанной около треугольника.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
Дано: АВС — данный треугольник; О — центр описанной около него окружности (рис. 30).
Доказать: О — точка пересечения серединных перпендикуляров.
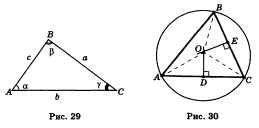
Доказательство. Треугольник АОС равнобедренный: у него стороны О А и ОС равны как радиусы. Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне АС и проходящей через ее середину. Точно так же доказывается, что центр окружности лежит на перпендикулярах к двум другим сторонам треугольника.
Замечание. Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
6 билет.
1) Определение . Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства
Противоположные стороны параллелограмма равны
| AB | = | CD | , | AD | = | BC | .
Противоположные углы параллелограмма равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
| AO | = | OC | , | BA | = | OD | .
Сумма углов, прилежащих к одной стороне, равна 180
Сумма всех углов равна 360°
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон:
пусть а — длина стороны AB, b — длина стороны BC, d1 и d2 — длины диагоналей; тогда d1^2+d2^2=2(a^2+b^2)
2) Окружность называется вписанной в треугольник, если она касается всех его сторон.
[П] Теорема о центре окружности, вписанной в треугольник.
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис.
Дано: АВС — данный треугольник; О — центр вписанной в него окружности; D, Е и F — точки касания окружности со сторонами треугольника (рис. 27).
Доказать: О — точка пересечения биссектрис.
Доказательство. Прямоугольные треугольники AOD иАОЕ равны по гипотенузе и катету. У них гипотенуза ОА — общая, а катеты OD и ОЕ равны как радиусы. Из равенства треугольников следует равенство углов OAD и ОАЕ. А это значит, что точка О лежит на биссектрисе треугольника, проведенной из вершины А. Точно так же доказывается, что точка О лежит на двух биссектрисах треугольника.
Дата добавления: 2020-12-12; просмотров: 88; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
