Определение перемещений при нескольких участках нагружения и

ИЗГИБ. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ИЗОГНУТОЙ ОСИ БАЛКИ

Под действием нагрузки балка искривляется. Сечения балки перемещаются перпендикулярно первоначально прямой оси балки и одновременно поворачиваются (рис. VII.1).

Перемещение центра тяжести сечения по направлению, перпендикулярному оси балки, называется прогибом балки в данной точке (сечении) и обозначается u.

Угол J, на который сечение поворачивается по отношению к своему первоначальному положению, называется углом поворота сечения.

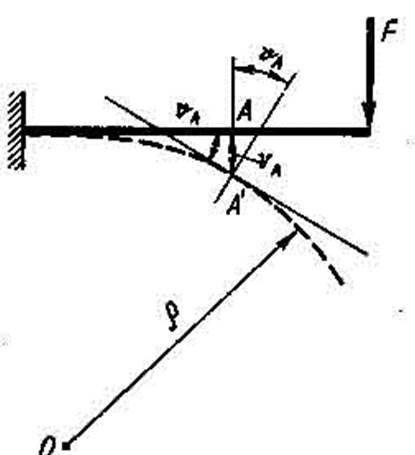
Учитывая, что повернувшееся сечение перпендикулярно изогнутой оси балки, заключаем, что вместо определения угла поворота сечения можно определять равный ему угол между касательной к данной точке изогнутой оси и первоначальной осью балки (рис. VII.1, где прогиб и угол поворота сечения даны для точки А).

Для определения деформаций балки воспользуемся уравнением

К = 1/ r = М / (Е I ), (VII.1)

связывающим кривизну оси балки с изгибающим моментом и жесткостью сечения балки (см. § 52).

Из курса математики известна следующая формула для кривизны линии:

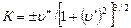(VII.2)
где ,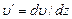

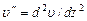
Подставляя это значение К в формулу (VII.1), получаем

(VII.3)

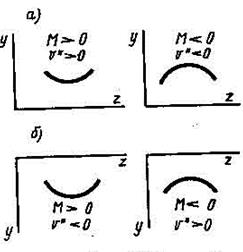Уравнение (VII.3) представляет собой точное дифференциальное уравнение изогнутой оси балки (упругой линии). Интегрирование этого нелинейного уравнения представляет большие трудности. Однако для большинства практических задач величиной ввиду малости деформаций по сравнению с единицей можно пренебречь.

Фактические значения углов поворота сечений балки порядка тысячных долей радиана. Если даже принять J = 0,01 рад, то и в этом случае величина J²=(u')² ничтожно мала по сравнению с единицей.

Рис. VII.

Отбрасывая (u')² в знаменателе формулы (VII. 3), получим приближенное дифференциальное уравнение изогнутой оси балки

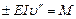(VII.4)

интегрирование которого не представляет затруднений. Выбор знака определяется принятой системой координат. Для системы координат, приведенной на рис. VII.2, а, имеем одинаковые знаки для кривизны и для момента М.

Следовательно, в этой системе координат следует пользоваться уравнением (VII. 4) в виде

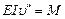(VII.5)

Для системы координат, принятой на рис. VII.2, б, имеем разные знаки для u" и М. Следовательно, в этом случае следует пользоваться уравнением (VI 1.4) в виде

(VII.6)

В дальнейшем будем пользоваться системой координат, показанной на рис. VII.2, а, и дифференциальным уравнением изогнутой оси, записанной в виде (VII.5).

Для вычисления углов поворота и прогибов u необходимо произвести интегрирование уравнения ( VII .5), что может быть выполнено тремя способами: аналитическим, графоаналитическим и графическим.

Рассмотрим аналитический способ.

Проинтегрировав уравнение (VII.5) один раз, получим уравнение углов поворота

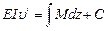(VII.7)

где С – постоянная интегрирования.

Интегрируя второй раз, получаем уравнение прогибов

(VII.8)

где D – вторая постоянная интегрирования.

Постоянные интегрирования С и D определяются из условий опирания балки (граничных условий). Так, для балки, заделанной одним концом (см. рис. VII.1), в месте заделки должны быть равны нулю и прогиб, и угол поворота сечения. Для балки, опертой по концам, прогиб должен быть равен нулю и на левом, и на правом конце.

Определив постоянные интегрирования, можно из уравнений (VII.7) и (VII.8) определить угол поворота и прогиб любого сечения.

Во многих случаях по эксплуатационным соображениям максимальные прогибы балок ограничиваются определенной величиной – допускаемым прогибом u_adm*. Допускаемый прогиб зависит от назначения сооружения или машины. Например, для подкрановых балок принимают

u _adm = (1/ 600 – 1/ 700 ) l

где l – пролет балки.

В машиностроении норма допускаемого прогиба колеблется в довольно широких пределах; в зависимости от назначения детали принимают

u _adm = (1/ 1000 – 1/ 300 ) l

Наибольшие углы наклона опорных сечений валов на роликовых подшипниках не должны превосходить 0,001 рад.

* В специальной технической и справочной литературе допускаемая стрела прогиба (максимального прогиба) обычно обозначается f_adm

Пример VII.1. Определить u_max и J_max для консоли нагруженной сосредоточенной силой на конце (рис. VII.3).

Р е ш е н и е. Начало координат поместим на левом конце балки. Изгибающий момент в сечении с абсциссой z определяем как момент внешних сил, расположенных между данными сечением и началом координат:

М_z = - Fz

Следовательно,

Интегрируем первый раз

Интегрируем второй раз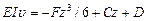

Для определения С и D имеем следующие условия:

1) при z = l u = 0; 2) при z = l J = u' = 0.

Из второго условия получаем С = Fl ² /2.

Из первого условия получаем 0 = Fl ³ /6+ Fl ² /2+ D , откуда D = – Fl ³ /3. Теперь можно определить u_max и J_max

Совершенно очевидно, что u_max и J_max имеют место при z = 0. Полагая в формулах z = 0, получаем

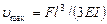; (VII.9)

Положительное значение угла поворота J указывает, что сечение поворачивается в направлении, противоположном движению часовой стрелки.

Отрицательное значение u показывает, что центр тяжести сечения перемещается вниз, т.е. в сторону отрицательных значений ординат u.

Обратим внимание на то, что (VII. 10)

и 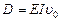(VII.11)

где u₀ – прогиб в начале координат, J₀ – угол поворота в начале координат.

Зависимости (VII.10) и (VII.11) всегда будут справедливы для балок, имеющих один участок нагружения, если вычислять изгибающие моменты от сил, расположенных между сечением и началом координат.

Это же остается в силе и для балок с любым числом участков нагружения, если вместо способа неопределенного интегрирования уравнения (VII.5) применить способ определенного интегрирования (см. § 59).

Нагружая образец по рис. VII.3, весьма просто определить модуль упругости материала.

Зная нагрузку F₁соответствующую прогиб конца образца – u₁ (определенный каким-либо прибором, например индикатором) можно из формулы (VI1.9) получить значение модуля упругости:

Определение модуля упругости путем испытания образцов на растяжение представляет более сложную процедуру.

Определение перемещений при нескольких участках нагружения и

Переменной жесткости балок.

УНИВЕРСАЛЬНЫЕ УРАВНЕНИЯ

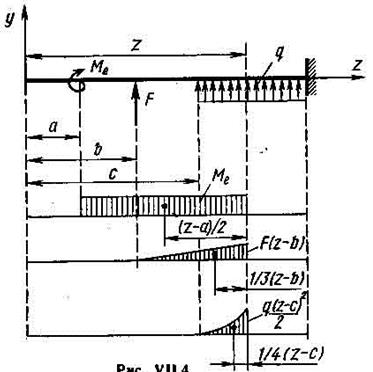
Если на балку действует сложная нагрузка (рис. VII. 4), то в этом случае на разных участках закон изменения изгибающих моментов будет выражаться различными уравнениями. Дифференциальное уравнение изогнутой оси придется составлять для каждого участка.

Число постоянных интегрирования будет равно удвоенному числу участков. Для определения этих постоянных всегда можно составить достаточное число уравнений, используя условия на опорах балки и условия на концах смежных участков, где прогибы и углы поворота равны между собой. Однако такой способ решения очень сложен.

Более простой способ решения получается, если вместо неопределенного интегрирования уравнения (VII.5) применить способ определенного интегрирования. При этом удается достигнуть удобной графоаналитической интерпретации решения.

Рассмотрим снова дифференциальное уравнение (VII.5). Проинтегрируем его один раз в пределах от нуля до z, приняв пока ЕI = const:

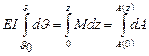(VII.12)

где dA = Mdz – дифференциал площади эпюры М (рис. VII.5).

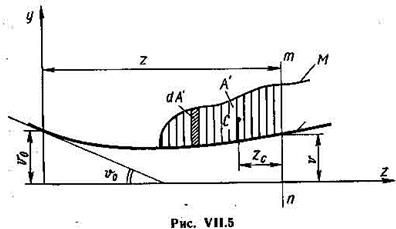
Выполнив интегрирование, получим из (VII. 12)

или 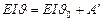(VII.13)

Здесь А (z) =А' – отсеченная площадь эпюры М, т.е. площадь эпюры, расположенная между началом координат и текущим сечением, в котором определяются перемещения; А (0) – отсеченная площадь для сечения, проходящего через начало координат, очевидно, равная 0.

Уравнение (VI 1.13) перепишем в виде (VII.14)

Проинтегрируем это уравнение от 0 до z:

. (VII.15)

Здесь dS = A(z) dz – дифференциал статического момента отсеченной площади эпюры М.

После интегрирования из (VII.15) получим

(VII. 16)

где статический момент отсеченной площади эпюры М относительно текущего сечения; S(0) – статический момент отсеченной площади эпюры М относительно сечения, проходящего через начало координат. Он равен нулю, так как A(0) =0.

Таким образом, для определения угловых и линейных перемещений при изгибе имеем формулы (VII.13) и (VII.16).

Если балка имеет различную жесткость на разных участках, то вместо формул (VII.13) и (VII.16) аналогично получим

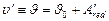(VII.17)

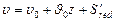(VII.18)

где А'_red – приведенная отсеченная площадь эпюры моментов, т. е. эпюры, ординаты которой поделены на EI. S¢_red – статический момент относительно текущего сечения приведенной отсеченной площади эпюры моментов.

В табл. VII.1 приведены наиболее часто встречающиеся эпюры изгибающих моментов с указанием их площадей и положения центра тяжести (z_с).

Таблица VII.1

Вид эпюры	Площадь эпюры	Расстояние от центра тяжести z_с
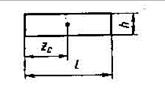
	hl	½ l
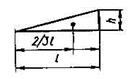
	½ hl	2/3 l
	1/3 hl	¾ l
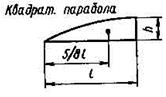
	2/3 hl	5/8 l

Правило знаков при пользовании формулами (VII.13) и (VII.16), а также формулами (VII.17) и (VII.18) следующее:

площадь А' принимается положительной, если эпюра М положительна;

площадь А' принимается отрицательной, если эпюра М отрицательна.

cтатический момент S¢_m_._n принимается положительным, если А' положительна; статический момент S¢_m_._n считается отрицательным, если А' отрицательна.

Если жесткость балки постоянна, то формулы (VII.13) и (VI1.16) можно представить в аналитической форме. Сделаем это для трех типов внешних сил, представленных на рис. VII.4. Строим эпюры изгибающих моментов от каждой нагрузки от-дельно.

По формулам (VII.13) и (VII.16) получим непосредственно следующие формулы, вычисляя площади и статические моменты (относительно текущего сечения) отсеченных площадей эпюр:

(VI1.19)

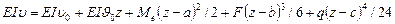(VI1.20)

При одновременном действии нескольких внешних сил уравнения для определения углов поворота и прогибов (на основании принципа независимости действия сил) имеют следующий вид:

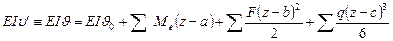(VI1.21)

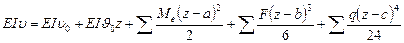(VII.22)

Эти уравнения называют универсальными уравнениями изогнутой оси балки. В них включены со своими знаками все внешние силы (включая опорные реакции), расположенные между началом координат и сечением с абсциссой z, в котором определяются перемещения. Внешние силы, показанные на рис. VII.4, включают в универсальные уравнения со знаком плюс, противоположно направленные внешние силы – со знаком минус.

Важно заметить, что последний член этих уравнений справедлив только в том случае, если распределенная нагрузка не обрывается ранее того сечения, где определяется u или J. Если же нагрузка обрывается, то следует продолжить ее до данного сечения, одновременно добавив нагрузку, равную по абсолютному значению, но обратного направления (рис. VII.6).

Недостаток универсальных уравнений состоит в том, что их нельзя непосредственно использовать для определения перемещений в балках, имеющих различную жесткость ЕI на разных участках.

В этих случаях следует применять общий метод определения перемещений – метод Мора (см. дальше) или пользоваться формулами (VII.17) и (VII.18).

Дата добавления: 2020-12-12; просмотров: 215; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!