Миноры и алгебраические дополнения элементов определителя.
Задание 1. (7.12. ПН)
Тема: Матрицы и действия с ними. Определитель матрицы.
Цель: сформировать умение выполнять арифметические действия с матрицами, находить определители матриц.
Теоретические сведения к практической работе
Матрицей называется прямоугольная таблица чисел, состоящая из m строк и n столбцов, которую записывают в следующем виде:
 .
.
Для обозначения матрицы используют прописные латинские буквы, для обозначения элементов матрицы – строчные латинские буквы с указанием номера строки и столбца, на пересечении которых стоит данный элемент. Запись «матрица B имеет размер m х n» означает, что речь идет о матрице, состоящей из m строк и n столбцов. Например, матрица 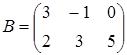 имеет размер 2 х 3. Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j -го столбца данной матрицы (в примере b 23 =5).
имеет размер 2 х 3. Далее, bij - обозначение элемента, стоящего на пересечении i-й строки и j -го столбца данной матрицы (в примере b 23 =5).
При ссылке на i -ю строку матрицы A используют обозначение Ai, при ссылке на j -й столбец – обозначение Aj.
Матрица, у которой число строк совпадает с числом столбцов, называется квадратной. Элементы a 11 , a 22 ,…, ann квадратной матрицы A (размера nxn ) образуют главную диагональ. Квадратная матрица, у которой отличные от нуля элементы могут стоять только на главной диагонали, называется диагональной. Диагональная матрица, у которой все элементы (главной диагонали!) равны 1, называется единичной. Наконец, квадратная матрица, у которой ниже (выше) главной диагонали находятся только нули, называется верхней (нижней) треугольной матрицей. Например, среди квадратных матриц размера 3 х 3
|
|
|
 ,
, 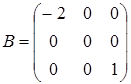 ,
, 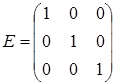 ,
, 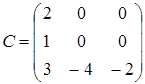
матрица A является верхней треугольной, B – диагональной, C – нижней треугольной, E – единичной.
Матрицы A , B называются равными (A = B), если они имеют одинаковый размер, и их элементы, стоящие на одинаковых позициях, совпадают.
Арифметические действия с матрицами.
1.Сложение матриц.
Операция сложения вводится только для матриц одинаковых размеров.
Суммой двух матриц А =  и В =
и В = 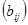 называется матрица С =
называется матрица С = 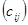 элементы, которой равны сумме соответствующих элементов матриц А и В, т.е
элементы, которой равны сумме соответствующих элементов матриц А и В, т.е 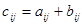 , где i=1,2,3,…,m, j=1,2,3,…,n.
, где i=1,2,3,…,m, j=1,2,3,…,n.
Пример 1. 
Аналогично определяется разность матриц.
Умножение матрицы на число.
Произведением матрицы А на число k называется матица kA, каждый элемент которой равен k  , i=1,2,3,…,m, j=1,2,3,…,n. т.е.
, i=1,2,3,…,m, j=1,2,3,…,n. т.е.
если А=  , то kA=
, то kA= 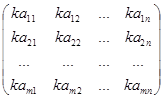
Умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
Пример 2. 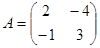 , k=2
, k=2
kA= 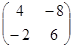
Матрица –А =(-1)∙А называется противоположной матрице А. Разность матриц А-В можно определить так: А-В=А+(-В).
Операция сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. переместительный закон сложения А+В=В+А,
|
|
|
2. сочетательный закон сложения (А+В)+С=А+(В+С),
3. А+О=А;
4. для любой матрицы А существует матрица –А, такая, что А+(-А)=0, т.е. матрица, противоположная А;
5. 1∙А=А;
6. α∙(А+В)=αА+αВ;
7. (α+β)∙А=αА+βА;
8. α∙(βА)=(αβ)∙А.
где где А, В, С - либо квадратные матрицы одного порядка n, либо прямоугольные матрицы одного размера m х n, а α и β – числа.
Пример 1. Найти 2 A - B, если  ,
,  .
.
Решение. Сначала умножаем матрицу A на число «2», затем матрицу B на число «-1», и, наконец, находим сумму полученных матриц:

Произведение матриц.
Операция умножения матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы 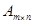 на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что  , где
, где 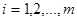 ,
, 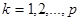 .
.
Получение элемента 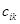 схематично изображается так:
схематично изображается так:


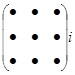
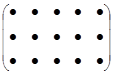 Вообще, чтобы получить элемент, стоящий на пресечении i -ой строки и j -го столбца матрицы произведения, нужно все элементы i -ой строки (
Вообще, чтобы получить элемент, стоящий на пресечении i -ой строки и j -го столбца матрицы произведения, нужно все элементы i -ой строки ( 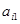 ,
, 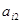 , …,
, …, 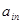 ) матрицы А умножить на соответствующие элементы j -го столбца (
) матрицы А умножить на соответствующие элементы j -го столбца ( 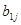 ,
, 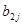 , …,
, …,  ) матрицы В и полученные произведения сложить.
) матрицы В и полученные произведения сложить.
Если матрицы А и В произвольного размера, то произведения АВ и ВА не всегда существуют.
|
|
|
Рассмотрим умножение квадратных матриц второго порядка. Пусть 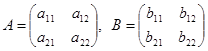 . Произведением этих матриц называется матрица
. Произведением этих матриц называется матрица 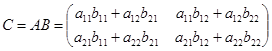
чтобы найти элемент 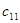 первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е.
первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е. 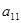 и
и 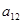 ) умножить на соответствующий элемент первого столбца матрицы В (т.е.
) умножить на соответствующий элемент первого столбца матрицы В (т.е. 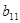 и
и 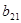 ) и полученные произведения сложить:
) и полученные произведения сложить: 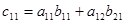 ;
;
чтобы получить элемент  первой строки и второго столбца матрицы С, нужно умножить все элементы первой строки (
первой строки и второго столбца матрицы С, нужно умножить все элементы первой строки ( 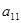 и
и 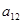 ) на соответствующие элементы второго столбца (т.е.
) на соответствующие элементы второго столбца (т.е. 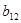 и
и  ) и полученные произведения сложить:
) и полученные произведения сложить: 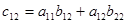 ;
;
аналогично находится элементы  и
и 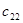 .
.
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко доказать, что А∙Е=Е∙А=А, где А-квадратная матрица, Е- единичная матрица того же размера.
Пример 3. Найти произведение матриц А и В, если
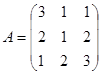 ,
, 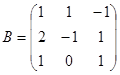
Решение. Так как матрица 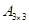 и матрица
и матрица 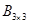 , то матрица произведения
, то матрица произведения 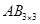 и содержит 9 элементов. Найдем каждый элемент матрицы-произведения:
и содержит 9 элементов. Найдем каждый элемент матрицы-произведения:
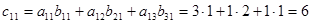
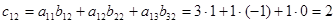
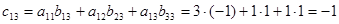


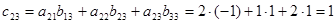

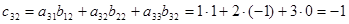
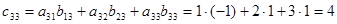

Пример 3. Найти произведение матриц А и В, если

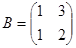
Решение. Произведение матриц А∙В не определенно, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определенно произведение В∙А: Так как матрица 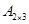 и матрица
и матрица  , то матрица произведения
, то матрица произведения 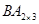 и содержит 6 элементов.
и содержит 6 элементов.
|
|
|
В∙А= 
Умножение матриц обладают следующими свойствами:
1. А∙(В∙С)= (А∙В)∙С;
2. А∙(В+С)=АВ+АС;
3. (А+В)∙С=АС+ВС;
4. α(АВ)=(αА)В.
5. 
Произведение AB можно определить только для матриц A размера m х n и B размера n х p, при этом AB = C, матрица C имеет размер m х p .
3. Транспонирование матриц.
Матрицей, транспонированной к матрице A размера m х n , называется матрица AT размера n х m , строки которой являются столбцами исходной матрицы.
Например, если 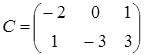 , то
, то 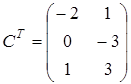 .
.
Пример 3. Найти 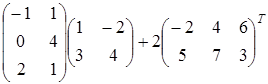 .
.
Решение. Воспользовавшись вычислениями, проведенными при решении примера, а также правилами умножения матрицы на число и сложения матриц, получим:
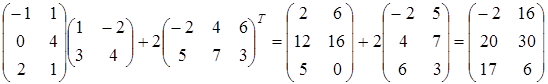 .
.
Матрицы A, B называются эквивалентными, если одна получена из другой путем элементарных преобразований.
4.Ранг матрицы.
Рангом матрицы A в дальнейшем будем считать число строк эквивалентной ей ступенчатой матрицы, используя обозначение r ( A ). Так, в рассмотренном выше примере 3.4 r ( A )=3, r ( B )=2. Можно доказать, что ранг матрицы A (размера mxn) не может быть больше  (например, для матрицы А размера 2 х 3
(например, для матрицы А размера 2 х 3 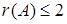 ). Кроме того, ранг матрицы не зависит ни от выбора ведущих элементов, ни от проводимых преобразований. Это свойство можно использовать при проверке. Так, в примере 3.4 после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала рассмотреть элемент b 12, а затем вычеркнуть третью строку, пропорциональную второй (
). Кроме того, ранг матрицы не зависит ни от выбора ведущих элементов, ни от проводимых преобразований. Это свойство можно использовать при проверке. Так, в примере 3.4 после перестановки первой и второй строки в матрице B можно в качестве ведущего сначала рассмотреть элемент b 12, а затем вычеркнуть третью строку, пропорциональную второй (  ):
):
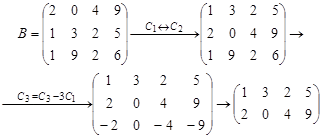
Вычисление определителей.
Определитель матрицы A размера 2 х 2 (определитель 2-го порядка) – это число, которое можно найти по правилу:
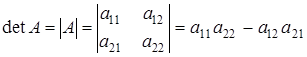
(произведение элементов, стоящих на главной диагонали матрицы, минус произведение элементов, стоящих на побочной диагонали).
Определитель матрицы A размера 3 х 3 (определитель 3-го порядка) – число, вычисляемое по правилу «раскрытие определителя по первой строке»:
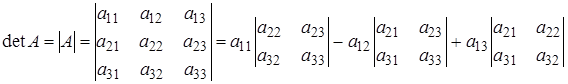
Пример 4. Найти определители: а)  б)
б) 
Решение: а) det  =
=  =
=  = 3·5 – (-2)·(-4) = 15 – 8 = 7
= 3·5 – (-2)·(-4) = 15 – 8 = 7
б) det  =
=  =
= 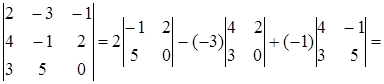

Миноры и алгебраические дополнения элементов определителя.
Минором  некоторого элемента
некоторого элемента  определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.
определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.
Например, Минор М12 , соответствующий элементу 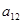 определителя
определителя  , получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.
, получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.  .
.
Пример 3. Записать все миноры определителя 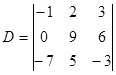
Решение.
 ,
, 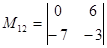 ,
,  ,
,
 ,
, 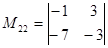 ,
, 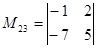 ,
,
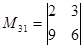 ,
, 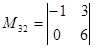 ,
,  .
.
Алгебраическим дополнением элемента  определителя называется минор
определителя называется минор  этого элемента, взятый со знаком
этого элемента, взятый со знаком  . Алгебраическое дополнение элемента
. Алгебраическое дополнение элемента  принято обозначать
принято обозначать 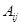 .
.
Таким образом, 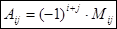 .
.
Знаки алгебраического дополнения Аij: 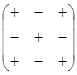
Пример 4. Найти алгебраические дополнения элементов 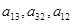 определителя
определителя 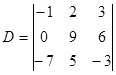 .
.
Решение.

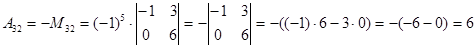
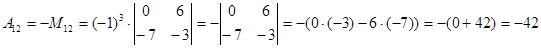 .
.
Обратная матрица.
Пусть А – квадратная матрица n-го порядка 
Квадратная матрица А-1 порядка n называется обратной матрицей для данной матрицы A, если 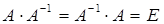 , где − E единичная матрица.
, где − E единичная матрица.
Квадратная матрица А называется вырожденной, если ее определитель det A равен 0 т.е. det A = 0.
В противном случае (det A≠0) матрица А называется невырожденной.
Обратная матрица 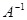 имеет те же размеры, что и матрица А.
имеет те же размеры, что и матрица А.
Теорема. Всякая невырожденная матрица А имеет обратную матрицу A-1, определяемую формулой 
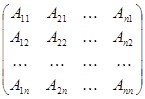
где A11, A12, …, Ann есть алгебраические дополнения соответствующих элементов a11, a12,…, ann матрицы А.
Правило вычисления обратных матриц n-го порядка
1. Находят определитель матрицы А т.е. detA.
2. Находят алгебраические дополнения всех элементов  матрицы А.
матрицы А.
3. Умножают полученную транспонированную матрицу на 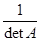 .
.

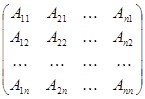
Нахождение обратной матрицы имеет большое значения при решении систем линейных уравнений и в вычислительных методах линейного программирования.
Пример 1. Дана матрица А = 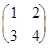 , найти А-1.
, найти А-1.
Решение.
1. det A = 4 - 6 = -2.
2. А11=4; А12= -3; А21= -2; А22=1
3. Таким образом, А-1= 
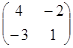 =
= 
Пример 2. Найти матрицу А-1, если 
Решение.
1. Вычислим определитель матрицы (см. выше, как находится определитель.)
det=5≠0, то матрица А невырожденная и имеет обратную матрицу А-1.
2. Вычислим алгебраические дополнения всех элементов матрицы А по формуле 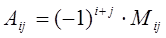 .
.
Знаки алгебраического дополнения Аij: 
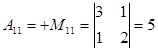
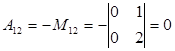
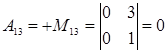
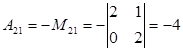
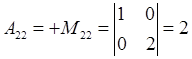
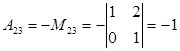
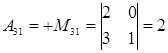
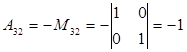

3. Подставляя найденные значения в формулу для А-1 получим:

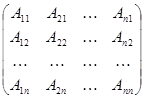


Дата добавления: 2021-01-20; просмотров: 148; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
