Графики обратных тригонометрических функций
Лекция 16
Тема «Обратные тригонометрические функции»
План лекции:
1. Свойство и графики тригонометрических функций.
2. Определение арксинуса.
3. Определение арккосинуса.
4. Определение арктангенса.
5. Определение арккотангенса.
Свойства и графики тригонометрических функций

1. Область определения – множество всех действительных чисел.
2. Область изменения (множество значений) – промежуток  .
.
3. Функция  нечетная:
нечетная:  .
.
4. Функция  периодическая. Наименьший положительный период равен 2p:
периодическая. Наименьший положительный период равен 2p:  .
.
5. Нули функции:  при
при  .
.
6. Промежутки знакопостоянства:
sin x > 0 при  ,
,
sin x < 0 при  .
.
7. Функция  возрастает при
возрастает при  и убывает при
и убывает при  .
.
8. Функция  принимает минимальные значения, равные -1, при
принимает минимальные значения, равные -1, при  и максимальные значения, равные 1, при
и максимальные значения, равные 1, при  .
.
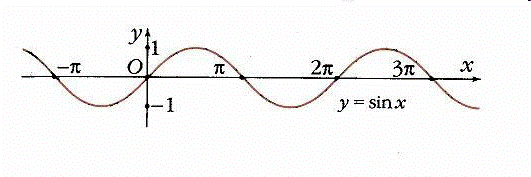
График функции  называют синусоидой.
называют синусоидой.

1. Область определения – множество всех действительных чисел.
2. Область изменения (множество значений) – промежуток  .
.
3. Функция  четная:
четная:  .
.
4. Функция  периодическая. Наименьший положительный период равен 2p:
периодическая. Наименьший положительный период равен 2p:  .
.
5. Нули функции:  при
при  .
.
6. Промежутки знакопостоянства:
cos x > 0 при  ,
,
cos x < 0 при  .
.
7. Функция  возрастает при
возрастает при  и убывает при
и убывает при  .
.
8. Функция  принимает минимальные значения, равные -1, при
принимает минимальные значения, равные -1, при  и максимальные значения, равные 1, при
и максимальные значения, равные 1, при  .
.

График функции  также называют синусоидой.
также называют синусоидой.
|
|
|

1. Область определения – множество всех действительных чисел, кроме чисел  .
.
2. Область изменения (множество значений) – множество всех действительных чисел.
3. Функция  нечетная:
нечетная:  .
.
4. Функция  периодическая. Наименьший положительный период равен p:
периодическая. Наименьший положительный период равен p:  .
.
5. Нули функции:  при
при  .
.
6. Промежутки знакопостоянства:
tg x > 0 при  ,
,
tg x < 0 при  .
.
7. Функция  возрастает в каждом из промежутков
возрастает в каждом из промежутков  .
.
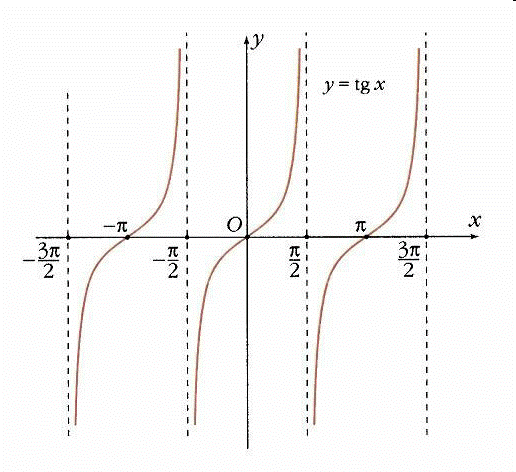
График функции  называют тангенсоидой.
называют тангенсоидой.

1. Область определения – множество всех действительных чисел, кроме чисел  .
.
2. Область изменения (множество значений) – множество всех действительных чисел.
3. Функция  нечетная:
нечетная:  .
.
4. Функция  периодическая. Наименьший положительный период равен p:
периодическая. Наименьший положительный период равен p:  .
.
5. Нули функции:  при
при  .
.
6. Промежутки знакопостоянства:
ctg x > 0 при  ,
,
ctg x < 0 при  .
.
7. Функция  убывает в каждом из промежутков
убывает в каждом из промежутков  .
.
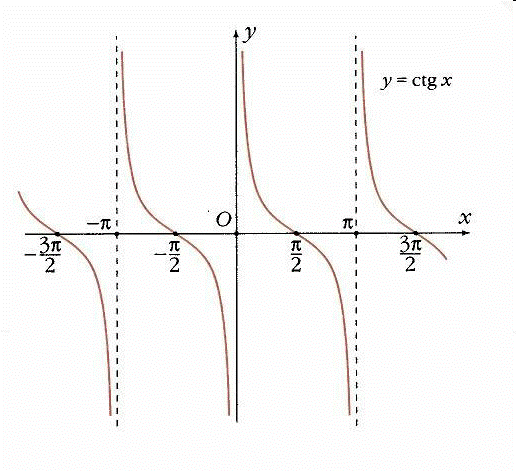
Синус, косинус, тангенс и котангенс часто называют основными тригонометрическими функциями.
Обратные тригонометрические функции
Определение. Арксинусом числа a называется число из отрезка  , синус которого равен a.
, синус которого равен a.
Определение. Функция  на отрезке
на отрезке  имеет обратную функцию, которая называется арксинусом и обозначается
имеет обратную функцию, которая называется арксинусом и обозначается  .
.
|
|
|
Функция  обладает следующими свойствами:
обладает следующими свойствами:
1)  - область определения.
- область определения.
2)  - область значения.
- область значения.
3)  , где
, где 
4) 
Пример 1. Найдите  .
.
Так как  , то
, то  .
.
Пример 2. Найдите 
Число (из промежутка  ), синус которого есть
), синус которого есть 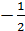 , равно
, равно 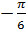 . Поэтому
. Поэтому

Функция  убывает на отрезке
убывает на отрезке  и принимает все значения от -1 до 1. Поэтому для любого числа a, такого, что
и принимает все значения от -1 до 1. Поэтому для любого числа a, такого, что  , на отрезке
, на отрезке  существует единственный корень b уравнения
существует единственный корень b уравнения  . Это число b называют арккосинусом числа a и обозначают
. Это число b называют арккосинусом числа a и обозначают  .
.
Определение. Арккосинусом числа a называется такое число из отрезка  , косинус которого равен a.
, косинус которого равен a.
Определение. Функция  на отрезке
на отрезке  имеет обратную функцию, которая называется арккосинусом и обозначается
имеет обратную функцию, которая называется арккосинусом и обозначается  .
.
Функция  обладает следующими свойствами:
обладает следующими свойствами:
1) 
2) 
3)  , где
, где 
4) 
Пример 3.  .
.
Пример 4.  .
.
На интервале  функция
функция  возрастает и принимает все значения из R. Тогда, по теореме о корне, для любого числа a из интервала
возрастает и принимает все значения из R. Тогда, по теореме о корне, для любого числа a из интервала  существует единственный корень b уравнения
существует единственный корень b уравнения  . Это число b называют арктангенсом числа a и обозначают
. Это число b называют арктангенсом числа a и обозначают  .
.
Определение. Арктангенсом числа a называется такое число из интервала  , тангенс которого равен a.
, тангенс которого равен a.
|
|
|
Определение. Функция  на промежутке
на промежутке  имеет обратную функцию, которая называется арктангенсом и обозначается
имеет обратную функцию, которая называется арктангенсом и обозначается  .
.
Функция  обладает следующими свойствами:
обладает следующими свойствами:
1) 
2) 
3)  , где
, где 
4) 
Пример 5.  .
.
Пример 6. 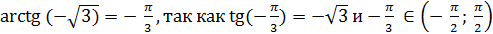 .
.
Функция котангенс на интервале  убывает и принимает все значения R . Следовательно, по теореме о корне, для любого числа a из интервала
убывает и принимает все значения R . Следовательно, по теореме о корне, для любого числа a из интервала  существует единственный корень b уравнения
существует единственный корень b уравнения  . Это число b называют арккотангенсом числа a и обозначают
. Это число b называют арккотангенсом числа a и обозначают  .
.
Определение. Арккотангенсом числа a называется такое число из интервала  , котангенс которого равен a.
, котангенс которого равен a.
Определение. Функция  на промежутке
на промежутке  имеет обратную функцию, которая называется арккотангенсом и обозначается
имеет обратную функцию, которая называется арккотангенсом и обозначается  .
.
Функция  обладает следующими свойствами:
обладает следующими свойствами:
1) 
2) 
3)  , где
, где 
4) 
Пример 7. 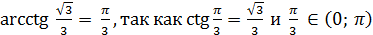 .
.
Пример 8. 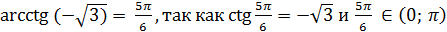 .
.
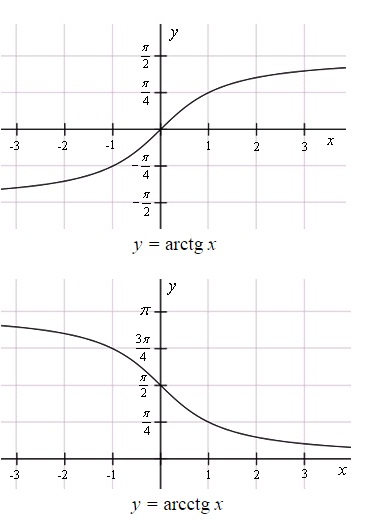
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x.

Пример 9. Найти значение выражения 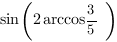
Обозначим  . По определению арккосинуса, y - это число из промежутка
. По определению арккосинуса, y - это число из промежутка  , косинус которого равен
, косинус которого равен  .
.
|
|
|
То есть нам известно, что  , и нам надо найти
, и нам надо найти 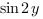 .
.
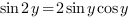 .
.
Значение  . С помощью основного тригонометрического тождества найдем значение
. С помощью основного тригонометрического тождества найдем значение 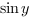 .
.
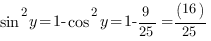 . Т.к.
. Т.к.  ,
, 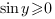
 , значит
, значит  .
.
Отсюда: 
Ответ: 0,96
Пример 10. Найти значение выражения 
Обозначим  . По определению арккотангенса, y - число из промежутка
. По определению арккотангенса, y - число из промежутка  , котангенс которого равен
, котангенс которого равен 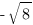 .
.
То есть нам известно, что 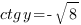 , и нам надо найти значение
, и нам надо найти значение 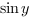 .
.
Т. к.  , значит, с учетом условия,
, значит, с учетом условия, 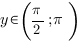 и
и 

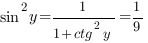
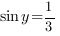
Ответ: 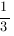
Контрольные вопросы:
1. Какие существуют тригонометрические функции?
2. Перечислите свойства тригонометрических функций.
3. Какие функции называются обратными тригонометрическими функциями?
4. Перечислите свойства обратных тригонометрических функций.
5. Изобразите графики обратных тригонометрических функций.
5. Вычислите:
а) 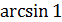 ;
;
б) 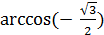 ;
;
в) 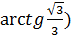 ;
;
г) 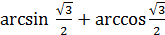 ;
;
д)  .
.
Дата добавления: 2021-01-20; просмотров: 152; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
