Рассмотрим интегралы типа 1-3
111 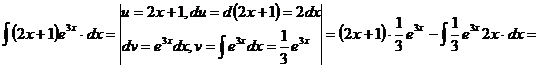
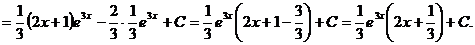 .
.
112 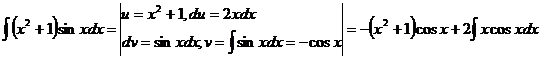
Для вычисления интеграла 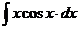 снова применяем метод интегрирования по
снова применяем метод интегрирования по
частям
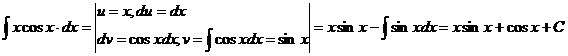
Сформируем окончательный ответ
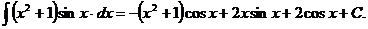 .
.
Рассмотрим интегралы типа 4-6
113 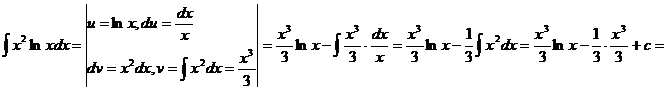
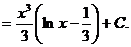 .
.
114 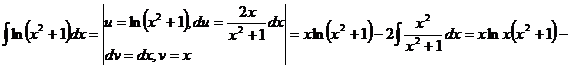
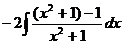
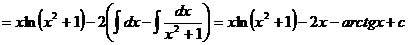 .
.
115 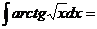 (применим способ подстановки)
(применим способ подстановки) 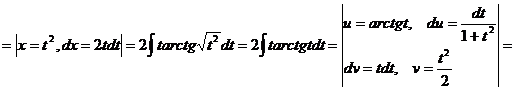
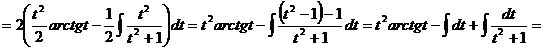
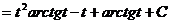 =
= 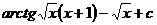
116
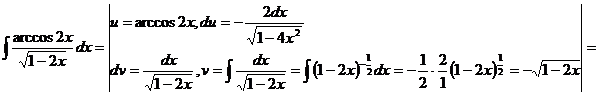
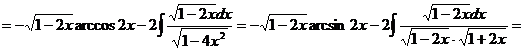
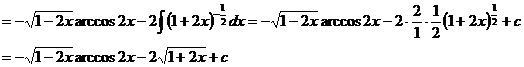
2.3.3 Рассмотрим интегралы, которые интегрируются по частям, но не являются типовыми (таблица 1)
117 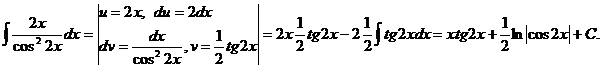 .
.
118
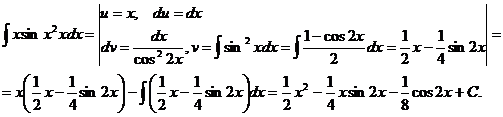
Выполните самостоятельно
119 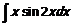 120
120 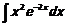
121 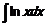 122
122 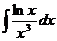
123 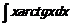 124
124 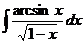
125 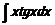 126
126 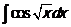
127 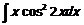 128
128 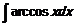
Циклические интегралы
129 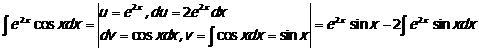 (*)
(*)
К последнему интегралу снова применим интегрирование по частям
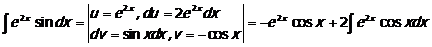
Подставим полученное выражение в равенство.(*)
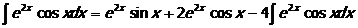
Замечаем, что образовался цикл. Чтобы выйти из цикла перенесем 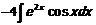 в левую часть, получаем:
в левую часть, получаем:
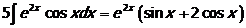 , откуда
, откуда 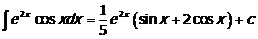 .
.
Дата добавления: 2021-01-20; просмотров: 41; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
