Варианты «Задачи о комивояжере»

Экономическая кибернетика

5-й курс 1-й семестр

     Вариант работы соответствует остатку от деления на 30 двух последних цифр зачетной книжки.

 

Задачі динамічного програмування

Основні принципи динамічного моделювання

 

У ЗЛП економічний процес вважається статичним, тобто не залежним від часу, тому оптимальне рішення знаходиться тільки на один етап планування.

Такі задачі називаються одноетапними чи однокроковими.

У задачах динамічного програмування економики процес залежить від часу (декількох етапів (періодів) часу), тому є ряд оптимальних рішень (послідовно для кожного етапу), що забезпечують оптимальний розвиток процесу в цілому.

Задачі ДП називаються багатоетапними або багатокроковими.

ДП являє собою математичний апарат, що дозволяє здійснити оптимальне планування багатокрокових керованих процесів і процесів, що залежать від часу.

Економічний процес називається керованим, якщо можна впливати на хід його розвитку. Керуванням називається сукупність рішень, прийнятих на кожному етапі з метою впливу на хід процесу (розподіл і перерозподіл засобів на кожному етапі).

Наприклад, випуск продукції будь-яким підприємством – керований процес, тому що він визначається зміною ресурсів, складу устаткування, обсягом постачань сировини і т. ін.

Початком етапу керованого процесу вважається процес ухвалення рішення ( про величину капітальних вкладень, заміні устаткування і т.ін.). Під етапом звичайно, розуміють господарський рік.

Плануючи багатоетапний процес, виходять з інтересів процесу в цілому., тобто при ухваленні рішення на окремих етапах завжди необхідно мати на увазі кінцеву мету.

 

Загальна постановка задачі динамічного програмування

Нехай планується діяльність деякої системи s промислових підприємств Р₁,Р₂,…,Рj,…,Р_n на деякий період часу Т , що складає з k господарських років t_i , де ( t=1,…,k), причому T=å t_i.

На початку періоду Т на розвиток підприємств виділені основні засоби D.

На початку кожного року виробляється фінансування всієї системи підприємств, тобто виділяється частина основних засобів. Відомий первісний стан системи S₀, який характеризується кількістю засобів, вже вкладених у підприємства і кінцевий стан S_k, сумою D.

Як варто розподілити по підприємствах і роках основні засоби D, щоб до кінця періоду Т сумарний доход W від усієї системи підприємств був би max?

 

Позначимо через x_ij суму, виділену на початку i-го року j-му підприємству (i=1,…,k),(j=1,…,n).

Припустимо, що засоби на i-му етапі розподілені, тобто обране визначене керування u₁, воно полягає в тому, що на початку i-го періоду підприємству Р₁ виділені засоби x_i1, підприємству Р₂ – x_i2 , і т.д.

Тоді вектор U_i= (x_i1,x_i2,…,x_in) визначає розподіл засобів на i-му кроці.

Сукупність виділених засобів (керувань) на k кроках виразжається системою векторів

U₁=(x_11, x₁₂,…,x_1n)

U₂=(x₂₁,x₂₂,…,x_2n)

…………..

U_k =(x_k1,x_k2,…,x_kn)

Сумарний доход за k років залежить від сукупності керувань, тобто є функцією від U₁,U₂,…,U_k :

W=W(U₁,U₂,…,U_k).

Завдання полягає в тому, що: на кожнім етапі необхідно вибрати таке керування, щоб сумарний доход від усієї системи підприємств був max.

Пример решения задачи о дилижансе

Постановка задачі: Знайти найкоротший маршрут з кінцевого пункту в початковий, якщо відома матриця транспортних витрат (см. табл 46).

Таблиця 46. Матриця транспортних витрат

	1	2	3	4	5	6	7	8	9	10
1		7	5	9
2					11	7	12
3					8	5	9
4					10	10	6
5							11	13
6							12		9
7										8
8										7
9										6
10

Алгоритм рішення:

f_n(s) – вартість, що відповідає стратегії min витрат для шляху від пункту s, якщо до кінцевого пункту залишилося n кроків.

j_n(s) - рішення, що дозволяє досягти f_n(s) .

Розраховувати будемо, користуючись рекурентним співвідношенням:

f_n (s) =min (c_sj+ f_n-1(j) ) по всем s и j на сети.

Рішенне :

Шаг 1

в       Из	10	f	j
7	8	10	8
8	7	10	7
9	6	10	6

Шаг 2

в       Из	7	8	9	f	j
5	11+8	13+7		19	7
6	12+8		9+6	15	9

Шаг 3

в      Из	5	6	7	f	j
2	11+19	7+15	12+8	20	7
3	8+19	5+15	9+8	17	7
4	10+19	10+15	6+8	14	7

Шаг 4

в       Из	2	3	4	f	j
1	7+20	5+17	9+14	22	3

 

Рисунок 19 Транспортная сеть

 

 

Ответ: F=22, кратчайший путь 1-3-7-10.

Варианты задачи 1

«Задача о дилижансе»

1. Построить сеть.

2. Ручной расчет.

 

 

Варианты:

1.

	1	2	3	4	5	6	7	8	9	10
1		10	15	14
2					11	7	12
3					8	5
4					10	10
5							11	13
6							12	9	6
7										10
8										2
9										6
10

2.

	1	2	3	4	5	6	7	8	9	10
1		12	17	16
2					10	9	15
3					7	7
4					9	12
5							14	10
6							15	6	6
7										12
8										4
9										8
10

3.

	1	2	3	4	5	6	7	8	9	10
1		8	7	11
2					11	7	12
3					8	5	9
4					14	15	6
5							11	13
6							12		9
7										8
8										7
9										6
10

4.

	1	2	3	4	5	6	7	8	9	10
1		9	12	9
2					16	17	12
3					18	15	19
4					10	10	16
5							11	13	12
6							12	10	9
7										3
8										7
9										6
10

5.

	1	2	3	4	5	6	7	8	9	10
1		5	2	4
2					6	7	2
3						5	9
4					5	4	6
5							11	13	12
6							4	4	5
7										8
8										7
9										8
10

6.

	1	2	3	4	5	6	7	8	9	10
1		29	22	22
2					26	15	12
3					21	15	19
4					20	10			10
5							11	13	12
6							12	10	9
7										23
8										17
9										23
10

7.

	1	2	3	4	5	6	7	8	9	10
1		9	12	9
2					4	12	12
3					8	15	19
4					7	13			8
5							11	13	12
6							12	10	9
7										3
8										7
9										6
10

8.

	1	2	3	4	5	6	7	8	9	10	11
1		12	8	7
2					4	5	8
3						7	8	9
4						6	8	7
5									11	10
6									10	9
7									12	8
8										7
9											6
10											9
11

 

 

9.

	1	2	3	4	5	6	7	8	9	10	11
1		9	11	7
2					7	8	10
3						7	9	5
4						6	8	7
5									10	8
6									10	11
7									12	4
8										7
9											6
10											9
11

10.

	1	2	3	4	5	6	7	8	9	10	11
1		24	23	17
2					17	18	10
3						17	19	25
4						26	18	17
5									10	8
6									10	11
7									12	14
8										7
9											16
10											19
11

11.

	1	2	3	4	5	6	7	8	9	10	11
1		36	31	37
2					37	28	30
3						27	29	5
4						26	28	17
5									20	18
6									19	11
7									22	14
8										17
9											6
10											9
11

12.

	1	2	3	4	5	6	7	8	9	10	11
1		9	11	7
2					7	8	10
3						7	9	5
4						6	8	7
5									10	8
6									10	11
7									12	4
8										7
9											6
10											9
11

13.

	1	2	3	4	5	6	7	8	9	10	11
1		9	10	7
2					7	8	10	12
3					9	7	9	5
4					6	6	8	7
5									10
6									10	11
7									12	4
8									11	7
9											16
10											19
11

14

	1	2	3	4	5	6	7	8	9	10	11
1		11	10	12
2					15	19	14	12
3					9	7	9	5
4					7	5	7	9
5									7
6									6	11
7									3	4
8									11	7
9											7
10											9
11

15.

	1	2	3	4	5	6	7	8	9	10	11
1		4	5	6
2					7	8	9	12
3					9	8	7	5
4					6	9	8	7
5									7
6									10	11
7									8	4
8									11	7
9											9
10											5
11

16.

	1	2	3	4	5	6	7	8	9	10
1		4	6	5
2					3	7	5
3					4	7	9
4					5	3	7
5								9	5
6								4	7
7								7	5
8										1
9										1
10

 

 

17.

	1	2	3	4	5	6	7	8	9	10
1		7	10	5
2					9	5	5
3					4	7	5
4					7	8	7
5								7	5
6								4	7
7								3	5
8										8
9										5
10

18.

	1	2	3	4	5	6	7	8	9	10
1		4	6	5
2					5	8
3					4		9
4						3	7
5								19	5
6								14	7
7								17	5
8										10
9										1
10

19.

	1	2	3	4	5	6	7	8	9	10
1		24	26	15
2					23	17	25
3					24	17	19
4					15	13	17
5								9	5
6								24	27
7								17	25
8										21
9										19
10

20.

	1	2	3	4	5	6	7	8	9	10
1		7	8	5
2					15	18
3					14		20
4						3	7
5								11	15
6								10	17
7								17	11
8										21
9										23
10

 

 

М етод ветвей и границ

К задачам целочисленного программирования относятся задачи комбинаторного вида, т.е. такие задачи в которых решение ищется на конечном множестве возможных значений переменных.

Например. Задача Коммивояжера (конечное число маршрутов (n!), задача о ранце (конечное число предметов), задача о максимальном потоке или кратчайшем пути в сетевых задачах (конечное число вершин графа).

Метод Гомори решения целочисленных задач линейного программирования не всегда дает удовлетворительные результаты, из-за слабой сходимости или вообще расходится из-за накопления ошибок вычислений. Другим методом, который вообще не связан с накоплением вычислительной погрешности, является метод ветвей и границ (МВиГ). МВиГ впервые был предложен Лендом и Дойгом в 1960 г., но получил широкое распространение в связи с применением этого метода в работе Литтла, Мурти, Суини и Кэрел в 1963 г., посвященной задаче о коммивояжере.

Идея метода состоит в следующем.

Рассмотрим задачу дискретного программирования:

требуется                             min ® Z=f(Х)                    (1)

при условии, что                 ХÎG                                   (2)

где G некоторое конечное множество.

Функция f(Х) и конечное множество G произвольного вида.

В основе метода лежат построения, позволяющие в ряде случаев существенно уменьшить число перебора вариантов. Введем обозначение G⁰ = G. Пусть нам удалось каким-либо образом найти такое значение x(G⁰), для которого можно сказать с уверенностью, что выполняется условие

                                   f(x) ³ x(G⁰), при xÎG⁰                 (3)

т.е. какое бы xÎG⁰ мы не взяли, значение f(x) всегда будет ³ x(G⁰), т.е. x(G⁰) является нижней граню для Z. Значение x(G⁰) может и не достигаться на G⁰, но если оно достигается, т.е. существует Х* такой, что f(Х*)= x(G⁰), т.е. Х* – оптимальное решение (f(x) не может быть > x(G⁰), к.к. это нижняя грань, но если мы вышли на эту нижнюю грань оставаясь в G⁰ то задача решена).

Производим разбиение G⁰ на подмножества так, чтобы

       , " i, j , i¹j                   (4)

Для каждого из полученных   определяем нижнюю грань 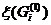. Причем, если

, то 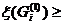 x(G0) нижняя грань x на множестве Gⁱ устанавливается более точно чем на G0.

Определяем:

                                                         (5)

Если существует план Х* Î  Þ f(x*)= , то Х* оптимальный план (существенным является не только то, что Х* Î , но и то, что Х* является планом (1)-(2)).

Если , , то множество  считается перспективным и его разбивают аналогично G⁰ (4) на подмножества 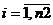. Переобозначим все множества  и  на .

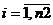                                   (6)

и переходим к (5) и т.д., до тех пор пока не будет найден оптимальный план. Здесь следует отметить тот факт, что в первую очередь ветвлению подвергаются только перспективные подмножества, при этом к ранее не перспективным можно вернуться на одном из последующих шагов, когда их оценка нижней грани будет £ оценки перспективного множества на этом шаге.

 

 

6

Пример. Дана сеть:

 

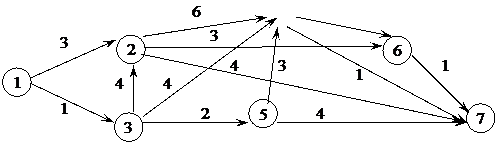
Требуется найти кратчайший путь из вершины 1 в 7, проходящий через вершины 4 или 5.

Планом задачи здесь является путь ведущий из вершины 1, через вершину 4 или 5 в вершину 7.

Шаг 1. Разбиваем множество всех путей ведущих из вершины 1 на 2 не пересекающихся подмножества:G¹ – множество всех путей проходящих из вершины 1 в вершину 2 и далее к вершине 7;G² – множество всех путей проходящих из вершины 1 в вершину 3 и далее к вершине 7.

В качестве оценки x возьмем длину ребер [1,2] и [1,3], т.к. это части пути, то длина полного пути всегда ³ xi.

		не проходят через 4 или 5

 

На третьем шаге получен путь [1,3,5,7], являющийся планом, т.е. ведущим из начальной вершины 1 в конечную – 7 и проходящий через вершину 5, но его оценка хуже двух других возможных маршрутов: x[1,3,2] = x[1,3,4] = 5 < f([1,3,5,7]) = 7, поэтому процесс продолжаем, ветвлением вершин [1,3,2] и [1,3,4].

На четвертом шаге получен план [1,3,4,7] и f(X) = 6 т.к. x(Gn)=6 и существует план с f(X)=6, то решение найдено.

Пути из всех остальных вершин с x=6 могут только увеличиваться, т.к. эти маршруты еще не являются планами.

МВиГ является универсальным методом решения комбинаторных задач. Сложность практического применения метода заключается в трудности нахождения способа ветвления множеств на подмножества и вычисления соответствующих оценок, которые зависят от специфики конкретной задачи.

Методом ветвей и границ решаются классические задачи «О коммивояжере» и «Задача Джонсона».

 

Задача о коммивояжере

Постановка задачи:

Коммивояжер должен обойти n городов А₁, А₂, …, А_n. Расстояния, между которыми известны и заданы в матрице расстояний.

Коммивояжер должен побывать в каждом городе по одному разу. Необходимо построить маршрут, наименьшей протяженности проходящий через все города .

 

Алгоритм решения задачи:

Обозначим через t маршрут перемещения коммивояжера по городам i₁, i₂, …, i_n, : t= (i₁, i₂, …, i_n)

или  t= {(i₁, i₂), (i₁, i₂), …, (i_{n-1, in}), (i_n, i₁)}

Длину маршрута t обозначим через l:

Рассмотрим расстояния от первого А1 города ко всем остальным:

c₁₂, c₁₃, …, c_1n.

Выберем из них минимальное:

h₁ =min(c₁₂, c₁₃, …, c_1n).

Аналогично можно для остальных строк матрицы найти такие же h_i. Так как маршрут должен выходить из каждого города, то величина

ω'=   является нижней гранью длины маршрута, т.е. меньше этого расстояния коммивояжер не пройдет, каков его маршрут ни был.

Вычтем из каждой строки матрицы «свое» h_i (выполним приведение матрицы по строкам).         

Здесь

c'_ij = c_ij - h_i или c_ij = c'_ij +h_i i=1,n, j=1,n.                                                                   

В результате приведения матрицы, в каждой ее строке появится хотя бы один нуль.

Запишем длину маршрута :

l(t)=l(i₁, i₂, …, i_n )= =  = + = + ω⁰,          

здесь сумма по всем (i,j) є t (по парам городов, входящим в маршрут),

а ω⁰= .

ω= ω⁰+ = + .                                                                      

Приведем матрицу по столбцам путем вычитания H_j из столбцов матрицы.

Здесь c"_ij = c'_ij - H _{j =} c_ij - h_i - H _j или c_ij = c"_ij + h_i + H _i i=1,n, j=1,n.            

Длина маршрута t теперь может быть записана в виде                           

l(t)=l(i₁, i₂, …, i_n )= 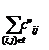+ ω.                                                                      

В маршрут необходимо включать пары городов таким образом, чтобы 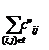была бы минимальной .

Пусть c"_pq =0. Непосредственный переход из города А_p в А_q, назовем «прямым»_, а переход из города А_p в А_q, через_, какой – то другой k-й город, назовем «окольным». Для каждой пары (p_,q), для которой c"_pq =0 оценим длину минимального окольного пути:

Θ(p_,q)= .                                                                        

Для включения в маршрут выберем ту пару городов, для которой c" _k,m = 0 и

Θ(_k,m)=max Θ(p_,q).                                                                                         

Разобьем множество всех маршрутов (а их n!) на два подмножества Х и У. В Х отнесем все те маршруты, которые содержат прямой переход из А_k в А_m, обозначим это множество (k,m), а в У – все маршруты, которые не содержат прямого перехода из А_k в А_m, и обозначим его как (k,m). Тогда для множества У можно определить оценку, как

ξ(У) = ω + Θ(_k,m),                                                                                           

Построим теперь оценку для множества маршрутов Х. Для этого с"_m,k=∞, так как есть переход из А_k в А_m, то переход из А_m в А_k запрещаем. Так как А_k включен в маршрут (из него коммивояжер больше выходить не будет), то этот город необходимо исключить из рассмотрения, т.е. вычеркнем k-ю строку из матрицы. Аналогично исключаем m-й столбец матрицы (город А_m включен в маршрут и, следовательно, этот город не должен больше выбираться, как город, в который коммивояжер еще раз будет входить). При этом следует сохранять первоначальную нумерацию строк и столбцов матрицы.

Приведем снова матрицу по строкам и столбцам. Определим величину

ω'= '+ ',о которой можно сказать, что коммивояжер, в связи с включением в маршрут перехода (k,m), должен будет дополнительно к минимально необходимому пути пройти еще расстояние ω', т.е. оценка длины всех маршрутов, входящих в множество Х равна

ξ(Х) = ω + ω'.                                                                                                 

Таким образом, дерево вариантов в этом случае примет вид:

         ξ(G⁰)= ω                             ξ(Х)                                                  

                    ξ(У)

 

 

 В этом дереве две вершины, выберем ту из них, у которой меньшая оценка. На первом шаге, вероятно, следует ожидать, что это будет вершина с множеством Х=(k,m). Дальше выполним снова ветвление выбранного множества на два подмножества, описанным выше способом . Этот процесс будет повторяться до тех пор, пока в матрице не останется две строки и два столбца, которые и завершат построение маршрута.

Пример решения задачи о коммивояжере:

Решение задачи:

	1	2	3	4	5	6	hi
1	-	41	60	39	46	10	10
2	31	-	59	16	1	51	1
3	29	51	-	14	42	50	14
4	32	12	52	-	16	26	12
5	16	39	15	60	-	57	15
6	15	30	38	47	36	-	15
Hj							67

	1	2	3	4	5	6	hi	αi
1	-	31	50	29	36	043	10	29
2	30	-	58	15	019	50	1	15
3	15	37	-	030	28	36	14	15
4	20	019	40	-	4	14	12	4
5	1	24	019	45	-	42	15	1
6	016	15	18	32	21	-	15	15
Hj	0	0	0	0	0	0	67
βj	1	15	18	15	4	14

 

 

	1	2	3	4	5	hi	αi
2	30	-	58	15	0	0
3	15	37	-	0	28	0
4	20	0	40	-	4	0
5	1	24	0	45	-	0
6	0	15	18	32	21	15
Hj
βj

 

	1	2	3	4	5	hi	αi
2	30	-	58	15	0	0
3	15	37	-	0	28	0
4	20	0	40	-	4	0
5	1	24	0	45	-	0
6	0	0	3	17	6	15
Hj	1	0	0	0	0	16
βj

	1	2	3	4	5	hi	αi
2	29	-	58	15	0­19		15
3	14	37	-	029	28		14
4	29	0­0	58	-	4		0
5	014	24	03	45	-		0
6	0	03	3	17	6		3
Hj
βj	14	0	3	15	4

 

 

	1	2	3	5	hi	αi
2	29	-	58	031	0	29
4	29	025	58	4	0	25
5	029	24	03	-	0	0
6	0	03	3	6	0	3
Hj	0	0	0	0	0
βj	29	0	3	4

	1	2	3	hi	αi
4	25	025	58	0	25
5	025	24	03	0	0
6	0	03	3	0	3
Hj	0	0	0	0
βj	25	0	3

 

	1	3	hi	αi
5	0	0	0
6	0	3	0
Hj	0	0	0
βj

Ответ:

L =83 Путь: 1-6-3-4-2-5-1

Варианты «Задачи о комивояжере»

 

 

1. Решить вручную

2. Решить с помощью пакета прикладных программ «KOMI»

 

 

Варианты:

1.

	1	2	3	4	5	6
1	-	4	10	13	4	8
2	2	-	9	7	6	7
3	8	5	-	5	5	9
4	5	8	5	-	7	10
5	6	4	4	9	-	4
6	5	1	4	8	3	-

2.

	1	2	3	4	5	6
1	-	51	21	21	24	59
2	43	-	6	10	9	15
3	54	13	-	33	21	35
4	16	37	15	-	55	43
5	19	12	26	60	-	30
6	3	44	42	46	30	-

3.

	1	2	3	4	5	6
1	-	41	60	39	46	10
2	31	-	59	16	1	51
3	29	51	-	14	42	50
4	32	12	52	-	16	26
5	16	39	15	60	-	57
6	15	30	38	47	36	-

 

4.

	1	2	3	4	5	6
1	-	31	40	25	47	12
2	22	-	44	26	20	22
3	37	17	-	43	11	55
4	11	35	9	-	40	26
5	50	4	11	34	-	36
6	18	7	28	25	26

 

5.

	1	2	3	4	5	6
1	-	48	4	46	0	0
2	24	-	26	38	0	19
3	53	50	-	0	26	14
4	12	34	0	-	23	4
5	0	0	41	14	-	14
6	35	7	31	0	32

6.

	1	2	3	4	5	6
1	-	20	28	12	39	32
2	21	-	15	9	17	27
3	30	25	-	45	29	47
4	7	52	40	-	15	1
5	60	46	11	5	-	34
6	11	45	14	21	30	-

 

7.

	1	2	3	4	5	6
1	-	19	40	30	15	9
2	56	-	14	57	12	8
3	42	4	-	28	33	24
4	1	12	5	-	21	16
5	21	16	38	52	-	59
6	51	1	17	22	29	-

 

8.

	1	2	3	4	5	6
1	-	40	100	130	40	80
2	20	-	90	70	60	70
3	80	50	-	50	50	90
4	50	80	50	-	70	100
5	60	40	40	90	-	40
6	50	10	40	80	30	-

 

9.

	1	2	3	4	5	6
1	-	56	26	66	29	64
2	48	-	11	15	14	20
3	59	18	-	38	26	40
4	21	42	20	-	60	48
5	24	17	31	65	-	35
6	8	49	47	51	35	-

 

10.

	1	2	3	4	5	6
1	-	46	65	44	51	15
2	36	-	64	21	6	55
3	34	56	-	19	47	55
4	37	17	57	-	21	31
5	21	44	20	65	-	62
6	20	35	43	52	41	-

11.

	1	2	3	4	5	6
1	-	36	45	30	52	17
2	27	-	49	31	25	27
3	42	22	-	48	16	60
4	16	40	14	-	45	31
5	55	9	16	39	-	41
6	23	12	33	30	31	-

 

	1	2	3	4	5	6
1	-	53	9	51	5	5
2	29	-	31	43	5	24
3	58	55	-	5	31	19
4	17	39	5	-	28	9
5	5	5	46	19	-	19
6	40	12	36	5	37	-

12.

	1			2		3		4		5		6
1	-			19		15		21		17		13
2	15			-		12		10		22		10
3	17			18		-		25		30		10
4	10			15		37		-		42		12
5	13			43		13		10		-		27
6	21			35		45		10		10		-
13.
		1	2		3		4		5		6
1		-	5		10		16		12		8
2		10	-		7		5		17		5
3		12	13		-		20		25		5
4		5	10		32		-		35		7
5		8	38		8		5		-		22
6		16	30		40		5		5		-

14.

	1	2	3	4	5	6
1	-	46	16	26	19	54
2	38	-	1	5	44	10
3	49	8	-	28	16	30
4	11	32	10	-	50	38
5	14	7	21	55	-	25
6	0	39	37	41	25	-

15.

	1	2	3	4	5	6
1	-	2	8	11	2	6
2	12	13	-	20	25	5
3	6	3	-	3	3	7
4	3	6	3	-	5	8
5	4	2	2	7	-	2
6	16	30	40	5	5	-

 

16.

	1	2	3	4	5	6
1	-	15	20	26	32	18
2	20	-	17	15	27	15
3	22	23	-	30	35	15
4	15	20	42	-	45	17
5	18	48	18	15	-	32
6	26	41	50	15	15	-

17.

	1	2	3	4	5	6
1	-	12	16	46	28	50
2	24	-	2	41	27	15
3	35	23	-	34	37	27
4	29	0	6	-	47	0
5	25	46	30	48	-	17
6	0	10	26	21	8	-

18.

	1	2	3	4	5	6
1	-	25	46	31	50	25
2	16	-	28	31	29	13
3	21	32	-	43	21	17
4	34	51	32	-	45	38
5	17	21	15	23	-	17
6	45	34	65	50	34	-

19.

	1	2	3	4	5	6
1	-	20	34	19	34	25
2	45	-	50	34	38	29
3	36	7	-	18	23	19
4	35	12	4	-	50	20
5	43	50	60	25	-	32
6	45	56	78	60	50	-

 

 

Задача Джонсона

Постановка задачи:

Необходимо обработать на трех станках n деталей. У всех деталей одна и та же последовательность обработки: 1-й, 2-й и 3-й станки. Времена обработки деталей на каждом станке приведены в таблице:

 

Детали Станки	1	2	…	n	Σ
Станок 1	a1	a2	…	an	Σ ai
Станок 2	b1	b2	…	bn	Σ bi
Станок 3	c1	c2	…	cn	Σ ci

 

Требуется составить оптимальную последовательность обработки всех n деталей на этих станках, т.е. такую последовательность запуска деталей на обработку, для которой время окончания обработки на всех станках будет наименьшим.

 

Алгоритм решения

 

Эта задача решается методом ветвей и границ, для этого введем ряд параметров:

σ_k={i_1, i₂, …,i_k} –произвольная последовательность из k деталей;

σ_k+1={σ_k , i_k+1} – произвольная последовательность из k+1 деталей;

A(σ_k), B(σ_k) и C(σ_k) - моменты окончания обработки последовательности деталей σ_k на первом, втором и третьем станках соответственно. Для последовательности σ_k+1 аналогичные моменты можно вычислить по рекурентным формулам:

A(σ_k+1) = A(σ_k)+a_k+1;

B(σ_k+1) = max(A(σ_k+1),B(σ_k)) + b_k+1;                                                                             

C(σ_k+1) = max(B(σ_k+1),C(σ_k)) + c_k+1.

Оценки:

δ_Ak= A(σ_k) +Σ a_i + min (b_i + c_i), по всем i Є σ_k (по всем деталям i не входящим в последовательность σ_k);

δ_Bk= B(σ_k) +Σ b_i + min c_i, по всем i Є σ_k;                                         

δ_Ck= C(σ_k) +Σ c_i, по всем i Є σ_k.

Величина δ_Ak имеет смысл оценки окончания обработки всей последовательности деталей на всех станках. Таким образом, можно сказать, что обработка всех деталей на трех станках завершится не ранее чем через δ_{Ak ,} δ_Bk и δ_Ck.

Введем обозначение

ξ = max(δ_Ak, δ_Bk, δ_Ck)_,                                                                                            

тогда С(σ_n) ≥ ξ,

т.е. величина ξ является оценкой (нижней границей) момента окончания всех n деталей на трех станках, при условии, что последовательность σ_k прошла обработку на всех станках. Очевидно, если взять другую последовательность (из других номеров) деталей, то величина ξ может быть иной. Та из последовательностей σ_k, для которой ξ имеет меньшее значение, является более предпочтительной для рассмотрения в первую очередь.

---

Дата добавления: 2021-01-20; просмотров: 317; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!