Физический смысл определенного интеграла
ПРАКТИЧЕСКАЯ РАБОТА №8
Тема: Вычисление определенных интегралов
Цель: закрепить навык вычисления определенных интегралов различными методами
уметь:
- применять основные методы интегрирования при решении задач;
знать:
- основные понятия и методы математического анализа;
Порядок выполнения работы:
1. Повторите теоретические материал по теме работы.
2. Выполните задание вашего варианта, с указанием используемых правил и формул.
3. Оформите работу и сделайте вывод
Таблица неопределенных интегралов.
1. 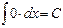 , где C – константа.
2. , где C – константа.
2.  3.
3.  , n¹–1.
4. , n¹–1.
4. 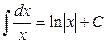 .
5. .
5. 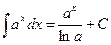 , ,  .
6. .
6. 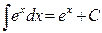 .
7. .
7. 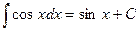 . .

| 8.  .
9. .
9.  .
10. .
10. 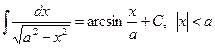 .
11. .
11.  .
12. .
12.  .
13. .
13.  .
В случае .
В случае 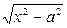 , предполагается что, , предполагается что,  . .
|
Определение:Приращение F ( b ) – F ( a ) любой из первообразных функций F ( x ) + C при изменении аргумента от x = a до x = b называется определённым интегралом от a до b функцииf ( x ) и обозначается:  (1)
(1)
Числа a и b называются пределами интегрирования, а – нижним, b – верхним. Отрезок [a ; b] называется отрезком интегрирования. Функция f ( x ) называется подынтегральной функцией, а переменная x – переменной интегрирования. Таким образом, по определению
 (2)
(2)
Данное равенство называется формулой Ньютона - Лейбница.
Свойства определённого интеграла:
1) Постоянный множитель можно выносить за знак интеграла, т.е. если A = const. то
|
|
|
 (3)
(3)
2) Определённый интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме их интегралов, т.е.  (4)
(4)
3) Если a<c<b, то 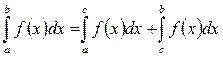
4) Если функция f ( x ) неотрицательная на отрезке [ a ; b ], где a < b, то 
5) Если f ( x )≥ g ( x ) для всех x € [ a ; b ], где a < b, то 
Рассмотрите примеры вычисления определенных интегралов, решенные методом непосредственного интегрирования
Непосредственное интегрирование предполагает использование основных свойств определенного интеграла и формулы Ньютона – Лейбница.
Приме 1: Вычислить  .
.
Решение: 
Пример2:Вычислить 
Решение: 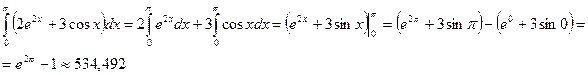
Пример3. Вычислить  .
.
Решение:
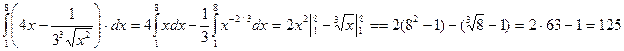
Геометрический смысл определенного интеграла
Если интегрируемая на отрезке [a;b] функция f ( x ) неотрицательна, то определённый интеграл  численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми x = a и x = b :
численно равен площади S криволинейной трапеции, ограниченной графиком функции f (x), осью абсцисс и прямыми x = a и x = b :

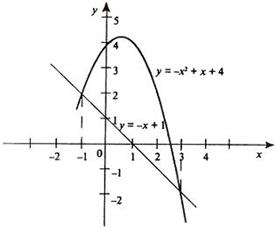
Пример 1. Вычислить площадь фигуры, ограниченной линиями  ,
,  .
.
Решение. Находим точки пересечения заданных линий.
|
|
|
Для этого решаем систему уравнений: 
 Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:
Для нахождения абсцисс точек пересечения заданных линий решаем уравнение:  или
или  .
.
Находим: x1 = – 2, x2 = 4. Итак, данные линии, представляющие собой параболу и прямую, пересекаются в точках A(-2; 0), B(4; 6).
Эти линии образуют замкнутую фигуру, площадь которой вычисляем по указанной выше формуле:
 .
.
По формуле Ньютона-Лейбница находим:
 .
.
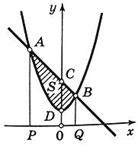
 Пример 2. Найти площадь фигуры, ограниченной линиями
Пример 2. Найти площадь фигуры, ограниченной линиями 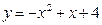 и
и  .
.
Решение. Найдем точки пересечения линий 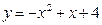 ,
,  , приравнивая ординаты линий:
, приравнивая ординаты линий: 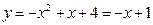 или
или  . Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
. Находим корни x1 = – 1 , x2 = 3 и соответствующие им ординаты y1 = 2, y2 = – 2.
По формуле площади фигуры получаем

Пример 3. Определить площадь, ограниченную параболой y = x2 + 1 и прямой x + y = 3.
Решение.
Решая систему уравнений  находим абсциссы точек пересечения x1 = – 2 и x2 = 1.
находим абсциссы точек пересечения x1 = – 2 и x2 = 1.
Полагая y2 = 3 – x и y1 = x2 + 1, на основании формулы  получаем
получаем 

Физический смысл определенного интеграла
1.  − сила, параллельная оси 0Х и ориентированная в положительном направлении оси 0Х, действующая на материальную точку при прямолинейном перемещении по промежутку [a, b]. Работа А силы
− сила, параллельная оси 0Х и ориентированная в положительном направлении оси 0Х, действующая на материальную точку при прямолинейном перемещении по промежутку [a, b]. Работа А силы  при этом равна:
при этом равна: 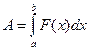 .
.
2.  − скорость неравномерного прямолинейного движения материальной точки.
− скорость неравномерного прямолинейного движения материальной точки.
|
|
|
Путь  , пройденный точкой за промежуток времени
, пройденный точкой за промежуток времени 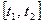 ,
,
при этом равен: 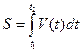 .
.
3.  − плотность неоднородного прямолинейного стержня с концами в точках
− плотность неоднородного прямолинейного стержня с концами в точках  .
.
Масса m такого стержня равна:  .
.
Задача о вычислении пути
Согласно физическому смыслу первой производной, производная функции в точке есть мгновенная скорость точки, т.е.  . Отсюда,
. Отсюда,  . Интегрируя полученное равенство в пределах от t1 до t2 получаем
. Интегрируя полученное равенство в пределах от t1 до t2 получаем

Тогда путь, пройденный точкой при неравномерном движении по прямой с переменной скоростью  (е) за отрезок времени [
(е) за отрезок времени [ 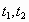 ]выражается интегралом
]выражается интегралом
 (1)
(1)
Пример 1. Скорость прямолинейного движения тела выражается формулой  = 2t+3t2(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
= 2t+3t2(м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
Решение.
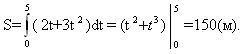
Пример 2. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью v  =(6t2+2t) м/с, второе – со скоростью v2=(4t+5) м/с. На каком расстояния друг от друга они окажутся через 5 с?
=(6t2+2t) м/с, второе – со скоростью v2=(4t+5) м/с. На каком расстояния друг от друга они окажутся через 5 с?
Решение. Искомая величина есть разность расстояний, пройденных телами за 5 с.

Таким образом, S=S1-S2= 275-75=200 (м).
Дата добавления: 2020-12-22; просмотров: 438; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
