Примеры универсальных исполнителей
Электронные ресурсы:
1. Машина Тьюринга. Введение. Понятие машины Тьюринга. Решение задачиhttps://www.youtube.com/watch?v=clrdEuTX9r8&list=PLT1KJddt96CF5dFATm3KXemsfPTKsxGS_
2.Машина Тьюринга. 2 часть. Решение задач.
https://www.youtube.com/watch?v=1pyrb01JKKM&list=PLT1KJddt96CF5dFATm3KXemsfPTKsxGS_&index=2.
Ссылка на эмулятор «Машина Тьюринга»: http://kpolyakov.spb.ru/prog/turing.htm
Алгоритм — это строго детерминированная последовательность действий, описывающая процесс преобразования объекта из начального состояния в конечное, записанная с помощью понятных исполнителю команд (Н. Д. Угринович)
Алгоритмом называют точный набор инструкций для исполнителя, который приводит к решению задачи за конечное время (К. Ю. Поляков)
Впервые необходимость формального понятия алгоритма возникла в связи с проблемой алгоритмической неразрешимости некоторых задач. Долгое время математики верили в возможность того, что все строго поставленные математические задачи могут быть алгоритмически решены, нужно только найти алгоритм их решения. Вера в универсальность алгоритмических методов была подорвана работой Курта Геделя (1931 год), в которой было показано, что некоторые математические проблемы не могут быть решены с помощью алгоритмов из некоторого класса. Этот класс алгоритмов определяется некоторой формальной конкретизацией понятия алгоритма. Встал вопрос: являются ли алгоритмически неразрешимыми эти проблемы только в рамках использованной Геделем модели алгоритма или же для решения этих проблем вообще нельзя придумать никакого алгоритма ни в каком смысле? Общность результата Геделя зависит от того, совпадает ли использованный им класс алгоритмов с классом всех алгоритмов в интуитивном смысле. Поэтому поиск и анализ различных уточнений и формализации алгоритма и соотношение этих формализаций с интуитивным понятием алгоритма является практически важным.
Интенсивный поиск универсального уточнения алгоритма предложил примерно 20 формальных конструкций алгоритмов, которые условно можно разбить на три типа:
- Алгоритмическиемашины (АМ).
- Функции, вычислимыеалгоритмом.
- Исчисления.
Алгоритмические машины (АМ)имеют единственный процессор, выполняющий небольшой набор очень примитивных действий,простую структуру данных (структуру памяти) в виде бесконечной ленты,простую логику (правила) управления процессором.
Основные АМ:
- Машина Тьюринга (МТ) предложена Тьюрингом в 1937 г.
- Машина Поста (МР) предложена Постом в 1937 г.
- Нормальный алгоритм Маркова (НАМ) предложен Марковым в 1953 г.

Машина Тьюринга-абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
Тьюринг назвал свое абстрактное механическое устройство "универсальной машиной", поскольку она должна была справляться с любой допустимой, то есть теоретически разрешимой задачей — математической или логической.
Данные должны были вводиться в машину на бумажной ленте, поделенной на клетки — ячейки.
Каждая такая ячейка либо содержала символ, либо была пустой.
Машина могла не только обрабатывать записанные на ленте символы, но и изменять их, стирая старые и записывая новые в соответствии с инструкциями, хранимыми в ее внутренней памяти.
Машина Тьюринга
Машина Тьюринга
(тренажер для изучения универсального исполнителя)
Машина Тьюринга состоит из каретки (считывающей и записывающей головки) и бесконечной ленты, разбитой на ячейки. Каждая ячейка ленты может содержать символ из некоторого алфавита A={a0,a1,…,aN}. Любой алфавит содержит символ «пробел», который обозначается как a0 или Λ. При вводе команд пробел заменяется знаком подчеркивания «_».
Машина Тьюринга — это автомат, который управляется таблицей. Строки в таблице соответствуют символам выбранного алфавита A, а столбцы — состояниям автомата Q={q0,q1,…,qM}. В начале работы машина Тьюринга находится в состоянии q1. Состояние q0 — это конечное состояние: попав в него, автомат заканчивает работу.
В каждой клетке таблицы, соответствующей некоторому символу ai и некоторому состоянию qj, находится команда, состоящая из трех частей:
- символизалфавита A;
- направление перемещения: > (вправо), < (влево) или.(на месте);
- новоесостояниеавтомата
В верхней части программы находится поле редактора, в которое можно ввести условие задачи в свободной форме.
Лента перемещается влево и вправо с помощью кнопок, расположенных слева и справа от нее. Двойным щелчком по ячейке ленты (или щелчком правой кнопкой мыши) можно изменить ее содержимое.
С помощью меню Лента можно запомнить состояние ленты во внутреннем буфере и восстановить ленту из буфера.
В поле Алфавит задаются символы выбранного алфавита. Пробел добавляется к введенным символам автоматически.
В таблице в нижней части окна набирается программа. В первом столбце записаны символы алфавита, он заполняется автоматически. В первой строке перечисляются все возможные состояния. Добавить и удалить столбцы таблицы (состояния) можно с помощью кнопок, расположенных над таблицей.
При вводе команды в ячейку таблицы сначала нужно ввести новый символ, затем направление перехода и номер состояния. Если символ пропущен, по умолчанию он не изменяется. Если пропущен номер состояния, по умолчанию состояние автомата не изменяется.
Справа в поле Комментарий можно вводить в произвольной форме комментарии к решению. Чаще всего там объясняют, что означает каждое состояние машины Тьюринга.
Программа может выполняться непрерывно (F9) или по шагам (F8). Команда, которая сейчас будет выполняться, подсвечивается зеленым фоном. Скоростьвыполнения регулируется с помощью меню Скорость.
Задачи для машины Тьюринга можно сохранять в файлах. Сохраняется условие задачи, алфавит, программа, комментарии и начальное состояние ленты. При загрузке задачи из файла и сохранении в файле состояние ленты автоматически записывается в буфер.
Головка всегда расположена над одной из ячеек ленты.
Работа происходит тактами (шагами).
Система исполняемых головкой команд предельно проста:на каждом такте она производит замену символа в обозреваемой ячейке ai символом aj
При этом возможны сочетания:
j = i – это означает, что в обозреваемой ячейке символ не изменился;
i_0, j = 0 означает, что хранившийся в ячейке символ заменяется пустым, т.е. стирается;
i =0, j_ 0 означает, что пустой символ заменяется непустым (с номером j в алфавите), т.е. производится вставка символа;
i j_ 0 соответствует замене одного символа другим.
Команды перемещений ленты
L («Left») на ячейку влево,
R («Right») на ячейку вправо
S («Stop») остаться на месте, т.е. адрес обозреваемой ячейки в результате выполнения команды может либо измениться на 1, либо остаться неизменным.
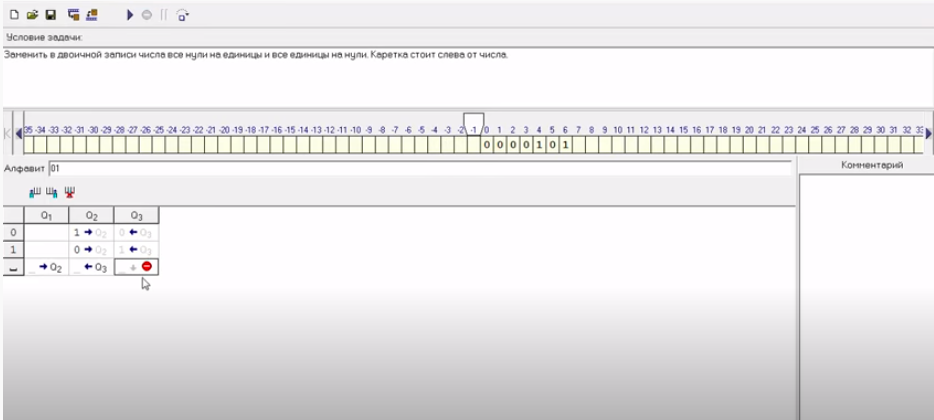
Пример 1.В двоичной записи заменить все нули на единицы, а единицы на нули. Каретка стоит слева от первого символа (их отделяет больше одного пустого символа!!!!).
Решение:
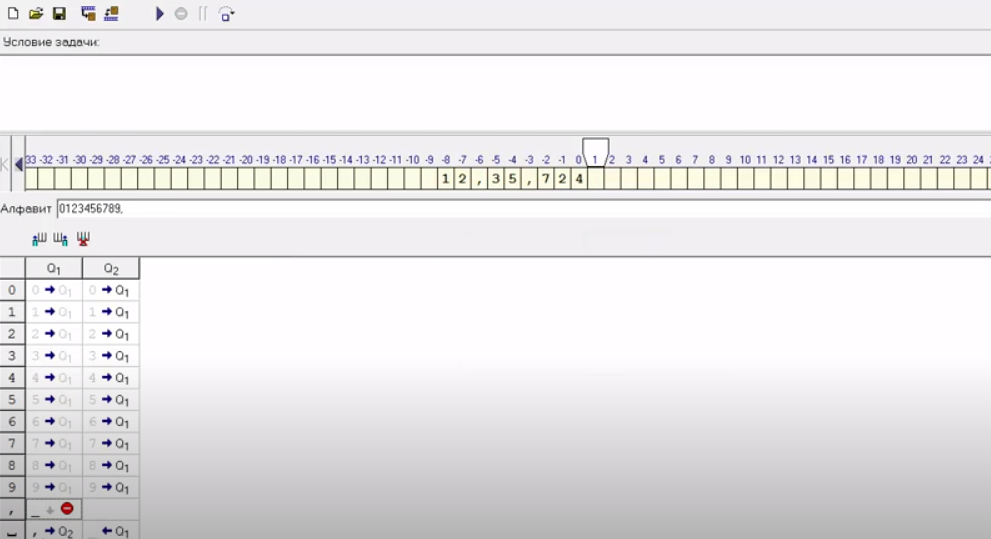
Пример. 2Записать три числа через пробел) а затем заменить эти пробелы на запятые (алфавит "0123456789,") Изначально каретка стоит первом слева не пустом символе.
Решение:
Машина Тьюринга - это модель компьютера
Отличия ЭВМ и машины Тьюринга. Главное отличие машины Тьюринга от ЭВМ – бесконечная лентаВ отличие от машины Тьюринга память реальных машин всегда конечна и ее ограничения удается преодолеть путем организации циклов if – если и for – делай до тех пор пока.
Совокупность всех команд, которые может выполнять машина, называется ее программой. Машина Тьюринга считается заданной, если заданы ее внешний и внутренний алфавиты, программа, начальная конфигурация и указано, какие из символов обозначают пустую ячейку и заключительное состояние.
Чтобы записать совокупность команд, нужно воспользоваться следующими правилами:
1) начальному шагу алгоритма ставится в соответствие q 0 - начальное состояние;
2) циклы реализуются так, что последнее действие цикла должно соответствовать переходу в то состояние, которое соответствует началу цикла;
3) соседним шагам алгоритма соответствует переход в смежные состояния, которые соответствуют этим пунктам;
4) последний шаг алгоритма вызывает переход в заключительное состояние.
Тезис Чёрча – Тьюринга: всякая вычислимая функция вычислима машиной Тьюринга.Другими словами, машина Тьюринга является формальным определением понятия алгоритма.
Тезис Чёрча – Тьюринга не является математическим утверждением. Это математическоеопределение. Его можно также воспринимать как закон природы: утверждение об окружающем нас мире, основанное на опыте.
Обсудим неформальные обоснования для этого тезиса. Во-первых, почему работа МТ реализуется алгоритмом? Это почти очевидно: каждый такт работы МТ состоит в выполненииочень простого набора действий: найти в таблице переходов строчку, которая начинается с текущего символа и текущего состояния; если таковой не нашлось, закончить работы и выделить из конфигурации результат; в противном случае заменить текущий символ на тот, который указан в найденной строчке, изменить состояние на указанное в найденной строчке, переместить головку влево, оставить на месте или переместить вправо в зависимости от указанной в найденной строчке команды движения. Фактически мы описали простые и однозначно понимаемые инструкции действий, что и есть алгоритм в неформальном понимании слова.
А исполнение алгоритма человеком в предельно упрощенном виде можно представить так.У человека есть карандаш, ластик, неограниченный запас листов бумаги и книжечка с инструкциями (собственно алгоритм). Бумага лежит в двух стопках, человек может выполнять действия лишь на одной стороне листа. Это аналог ленты машины. Действия определяются номером страницы в книге инструкций (состояние МТ) и содержимым верхнего листа бумаги (символ алфавита в ячейке, на которую смотрит головка). Чтобы действие было однозначно понимаемым, разных содержимых листа бумаги должно быть конечное число. Вот таким образом и приходим к формальному определению.
Универсальный исполнитель – это исполнитель, который может моделировать работу любого другого исполнителя. То есть, для любого алгоритма, написанного для любого исполнителя, существует эквивалентный алгоритм для универсального исполнителя. Система команд такого исполнителя должна быть как можно проще – так его будет проще использовать в доказательствах.
Примеры универсальных исполнителей
· МашинаТьюринга
· Машина Поста
· НормальныеалгорифмыМаркова
Алгоритмическая машина Поста
Машина Поста — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом (Emil L.Post), которая отличается от машины Тьюринга большей простотой. Обе машины «эквивалентны» и были созданы для уточнения понятия «алгоритм».
Абстрактная машина Поста состоитиз бесконечной ленты, разделенной на равные секции, считывающе-записывающей головки.
Каждая секция может быть либо пуста (т.е. в нее ничего не записано), либо заполнена (отмечена – т.е. в нее записана метка).
Состояние ленты и информация о положении головки характеризуют состояние машины Поста.
За один такт (его называют шагом) головка может сдвинуться на одну секцию вправо или влево и поставить или удалить метку.
Работа машины Поста заключает в переходе от одного состояния машины к другому в соответствии с заданной программой, которая строится из отдельных команд.
Структура команды
- Каждая команда имеет следующую структуру
- xKy,
- x – номер исполняемой команды;
- K – указание о выполняемом действии;
- y – номер следующей команды (наследника).
- Комментарий к примеру
Последовательное исполнение команд 1 и 2 приводит к тому, что головка за два такта работы машины сдвигается на одну позицию вправо.Это передвижение продолжается до тех пор, пока после очередного сдвига под головкой не окажется пустая ячейка – тогда по команде 3 в нее будет поставлена меткаи по команде 4 машина остановится. Если данные условия не выполняются, происходит безрезультатная остановка машины, т.е. остановка до получения запланированного результата.
Дата добавления: 2020-12-22; просмотров: 1066; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
