Примеры для самостоятельного решения
СЕМИНАР 13
Несобственные интегралы
При изучении определённого интеграла от функции f (x) требуется, чтобы функция f (x) удовлетворяла следующим условиям:
· была определена на конечном отрезке [a;b];
· была непрерывна на отрезке [a;b].
Если нарушено хотя бы одно из указанных условий, то речь будет идти о несобственных интегралах первого и второго рода.
Интегралы с бесконечными пределами
Пусть функция f (x) определена и непрерывна на промежутке [a;+¥) или (–¥;a] или (–¥;+¥).
Определение 1. Если существует конечный предел  , то этот предел называется несобственным интегралом от функции f(x) на бесконечном промежутке [a;+¥) первого рода, обозначается
, то этот предел называется несобственным интегралом от функции f(x) на бесконечном промежутке [a;+¥) первого рода, обозначается 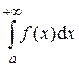 и в этом случае считается, что интеграл сходится. Если
и в этом случае считается, что интеграл сходится. Если 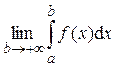 не существует или равен ¥, то считается, что интеграл
не существует или равен ¥, то считается, что интеграл 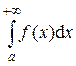 расходится.
расходится.
Аналогично определяются интегралы:

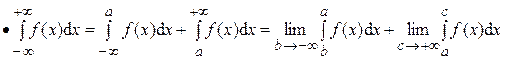
Если пределы конечные, то соответствующий интеграл считают сходящимся, а если хотя бы один из пределов не существует или бесконечный, то интеграл считают расходящимся.
Интегралы от разрывных функций
1) Пусть функция y = f (x) определена и непрерывна на отрезке [a;b], а в точке x = b либо не определена, либо имеет разрыв. Такую точку x = b
будем называть особой точкой функции f (x).
Определение 2. Если существует конечный предел  , то он называется несобственным интегралом второго рода от функции f(x) на отрезке [a;b] и обозначается символом
, то он называется несобственным интегралом второго рода от функции f(x) на отрезке [a;b] и обозначается символом 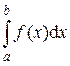 . При этом говорят, что несобственный интеграл
. При этом говорят, что несобственный интеграл  сходится и записывается равенство:
сходится и записывается равенство:
|
|
|
 .
.
Если конечный предел не существует или он бесконечный, то говорят, что несобственный интеграл  расходится.
расходится.
2) Пусть функция y = f (x) определена и непрерывна на отрезке [a;b], а в точке x = a либо не определена, либо имеет разрыв. Такую точку x = a называют особой точкой функции f (x).
Определение 3. Если существует конечный предел  , то он называется несобственным интегралом второго рода от функции f (x) на отрезке [a;b] и обозначается символом
, то он называется несобственным интегралом второго рода от функции f (x) на отрезке [a;b] и обозначается символом 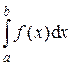 .
.
При этом говорят, что несобственный интеграл 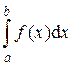 сходится и записывается равенство:
сходится и записывается равенство:
 .
.
Если конечный предел не существует или бесконечен, то говорят, что несобственный интеграл 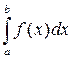 расходится.
расходится.
Замечание. Если функция f(x) имеет разрыв в некоторой точке x = c внутри отрезка [a;b], то по определению полагают:
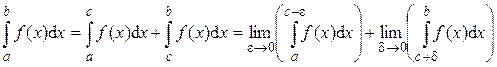
при условии, что оба предела в правой части существуют, и e иd не зависят друг от друга. Этот интеграл также называют несобственным интегралом второго рода от функции f (x) на отрезке [a;b] и обозначается символом:
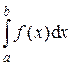 .
.
Сходимость или расходимость такого интеграла зависит от существования или не существования конечного предела.
|
|
|
Примеры с решениями
Пример 1. Исследовать на сходимость несобственный интеграл 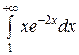
Решение.
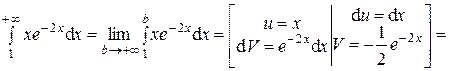
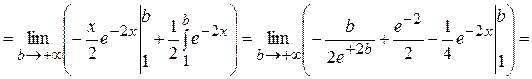
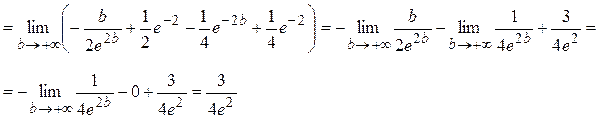
Так как получили конечное число, то интеграл  сходится и равен
сходится и равен 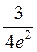 .
.
Ответ:  .
.
Пример 2. Исследовать на сходимость 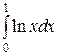
Решение.
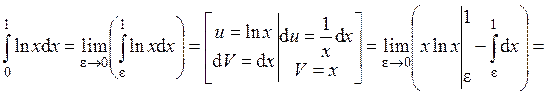
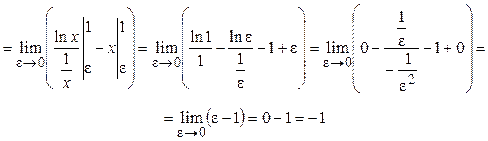
Так как получили конечное число, то 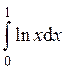 сходится и равен –1.
сходится и равен –1.
Ответ: 
Пример 3. Исследовать на сходимость 
Решение.

Так как получили конечное число, то 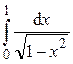 сходится и равен
сходится и равен 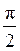 .
.
Ответ: 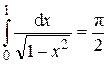 .
.
Пример 4. Исследовать на сходимость 
Решение.

Так как получили бесконечность, то  расходится.
расходится.
Ответ: 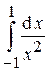 расходится.
расходится.
Примеры для самостоятельного решения
1.  7.
7. 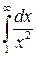
2.  8.
8. 
3. 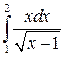 9.
9. 
4. 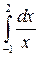 10.
10. 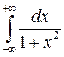
5. 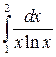 11.
11. 
6. 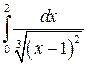 12.
12. 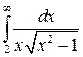
Ответы
1. 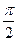 ; 2. расходится; 3.
; 2. расходится; 3. 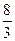 ; 4. расходится; 5. расходится; 6. 6; 7. 1; 8. расходится; 9.
; 4. расходится; 5. расходится; 6. 6; 7. 1; 8. расходится; 9.  ; 10. расходится; 11. 1; 12.
; 10. расходится; 11. 1; 12.  .
.
Дата добавления: 2020-12-22; просмотров: 38; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
