Примеры для самостоятельного решения
СЕМИНАР 10
Интегрирование рациональных дробей
Разложение рациональной дроби на сумму простых дробей
Определение 1. Рациональной дробью называется отношение двух многочленов:



Определение 2. Рациональная дробь называется правильной, если m < n . В противном случае (если m ³ n ) она называется неправильной.
Определение 3. Простыми рациональными дробями называются дроби следующих четырех типов:
I . 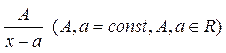 ,
,
II.  ,
,
III.  ,
,
IV. 
Теорема 1. Всякую неправильную рациональную дробь можно представить в виде суммы целой части (многочлена) и правильной рациональной дроби.
Теорема 2. Любую правильную рациональную дробь можно единственным образом представить в виде суммы конечного числа простых рациональных дробей.
Разложение правильной рациональной дроби  (m < n) на сумму простых дробей можно выполнить по следующей схеме:
(m < n) на сумму простых дробей можно выполнить по следующей схеме:
· Найти корни многочлена Qn(x ) и представить его в виде произведения простых множителей:
 ,
,
где  ,
, 
 ,
, 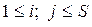
 ,
, 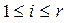
 ,
, 
· Записать разложение дроби с неопределёнными коэффициентами:


· Определить коэффициенты
 ,
,
суммарное число которых равно n, методом неопределённых коэффициентов.
Для этого необходимо всё разложение привести к общему знаменателю и приравнять числитель полученной дроби к Pm(x). Приравнивая в этих многочленах коэффициенты при одинаковых степенях x, получим систему из n линейных уравнений с n неизвестными. Эта система имеет единственное решение – искомые коэффициенты.
|
|
|
Интегрирование простых дробей
Задача интегрирования рациональной дроби сводится к интегрированию простых дробей четырёх типов.
I тип. 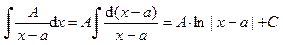
II тип. 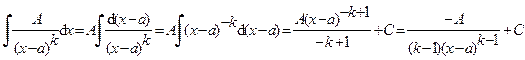

III тип. 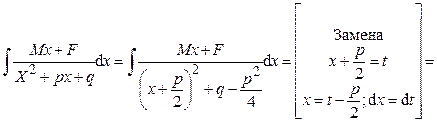
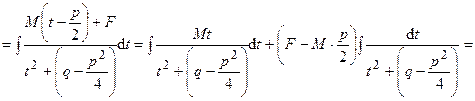


Интегрирование дроби IV типа проводится аналогично интегрированию дроби III типа.
Итак, любая рациональная дробь интегрируема. Для этого необходимо выполнить следующие шаги:
1) Выделить целую часть дроби, если дробь является неправильной, т.е. представить в виде:
 ,
,
где T m – n(x) и R r(x) – многочлены степени m – n и r соответственно (причём r < n).
2) Разложить правильную рациональную дробь  на сумму простых дробей.
на сумму простых дробей.
3) Вычислить интегралы от многочлена T m – n(x) и каждой из простых дробей, полученных на шаге 2).
Примеры с решениями
Пример 1. Найти интеграл 
Решение.
1) Дробь  – неправильная рациональная дробь. Выделим её целую часть:
– неправильная рациональная дробь. Выделим её целую часть:

Поэтому можно записать:
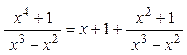 .
.
2) Полученную правильную дробь  разложим на сумму простых дробей:
разложим на сумму простых дробей:



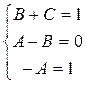
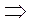

Отсюда следует: 
 .
.
Значит, подынтегральную рациональную дробь можем представить в виде:
 .
.
3) Найдём интеграл:

Ответ: 
Пример 2. Найти интеграл 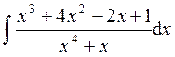
|
|
|
Решение.
1) Разложим подынтегральную правильную дробь на сумму простых дробей

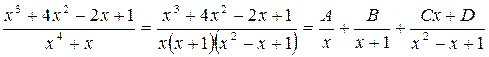
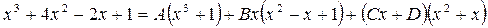


Отсюда следует:
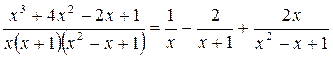
Найдем интеграл:
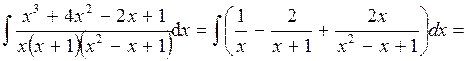

Последний интеграл находим по правилу, указанному в интегрировании дроби третьего типа. Выделяем полный квадрат в знаменателе
 и выполняем замену
и выполняем замену 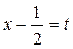 .
.


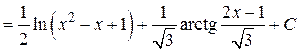 .
.
Подставляя найденный интеграл I в предыдущее выражение искомого интеграла, найдём
 .
.
Примеры для самостоятельного решения
1. 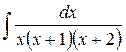
2. 
3. 
4. 
5. 
6. 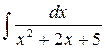
7. 
8. 
9. 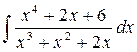
10. 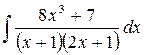
11. 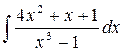
12. 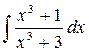
13. 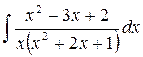
14. 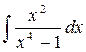
15. 
16. 
17. 
18. 
19. 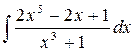
20. 
Ответы
1.  ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4. 
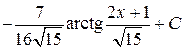 ; 5.
; 5.  ; 6.
; 6.  ; 7.
; 7.  8.
8.  ; 9.
; 9. 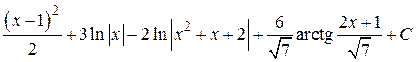 ; 10.
; 10. 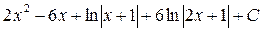 ; 11.
; 11. 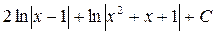 ;
;
12. 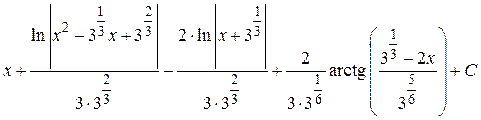 ;
;
13.  ; 14.
; 14.  ; 15.
; 15.  ; 16.
; 16.  ; 17.
; 17. 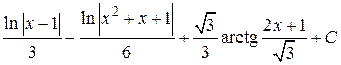 ; 18.
; 18. 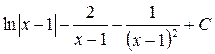 ; 19.
; 19.  ; 20.
; 20.  .
.
Дата добавления: 2020-12-22; просмотров: 43; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
