Доверительные интервалы и доверительная вероятность

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.

В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.

Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.

Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.

Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.

Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.

Пусть для генерального параметра a получена из опыта несмещенная оценка a*. Нужно оценить возможную при этом ошибку. Назначим достаточно большую вероятность β – такую, что событие с этой вероятностью можно считать практически достоверным, и найдем такое значение ε для которого

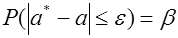(5.8.1)

При этом диапазон практически возможных значений ошибки, возникающей при замене а на а* , будет 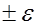, большие по абсолютной величине ошибки будут появляться только с малой вероятностью

α=1-β

называемой уровнем значимости или риском. Уровень значимости часто выражают в процентах. Иначе формулу ( (5.8.1* ) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах

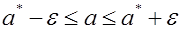
Вероятность β называется доверительной вероятностью, доверительным уровнем или надежностью, т.к. она характеризует надежность полученной оценки.

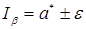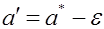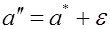Интервал называется доверительным интервалом. Границы интервала и доверительными границами. Доверительный интервал при данной доверительной вероятности определяет точность оценки параметра.

При этом отметим следующее. Ранее мы рассматривали вероятность попадания случайной величины на заданный (неслучайный) интервал. В данном случае дело обстоит иначе: величина ане случайна, зато случаен интервал I _b . Случайно его положение на числовой прямой, определяемое его центром а ^*, случайна и длина интервала 2 e, так как величина e вычисляется, как правило, по опытным данным, т.е. по результатам эксперимента. Поэтому в рассматриваемом случае удобно толковать интервал I как вероятность того, что случайный интервал I _b накроет величину а.

Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра внутри доверительного интервала: чем больше величина β, тем больше и ε (т.е. с чем большей вероятностью мы хотим гарантировать полученный результат, тем в большем интервале он должен находиться).

Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.

Обычно на практике фиксируется на определенном уровне значение доверительной вероятности (0.9, 0.95, 0.99, 0.999). Исходя из этого значения, определяют доверительный интервал результата I_β .

ППри построении доверительного интервала решается задача об абсолютном отклонении:

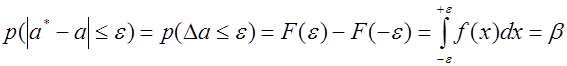(5.8.2.)

Таким образом, если известен закон распределения оценки a*, то задача определения доверительного интервала решается довольно просто.

Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины с известным генеральным стандартом σ_х.

Понятие генерального стандарта тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям

(ПРИМЕР: класс точности прибора K = abs ( a _max – a *)/ a_max =0.01 (1%) манометр с максимальным значением давления по шкале 100 кгс/см², абсолютная погрешность прибора Δ a = abs ( a - a *) =100*0.01=1ат Δ a =2σ_х, следовательно, σ_х=0,5 ат).

Пусть имеется выборка объема n значений случайной величины. Оценкой m_x является среднее выборки:

Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально можно показать, что 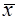также имеет нормальное распределение с математическим ожиданием m_x и средним квадратическим отклонением 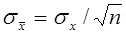. Тогда

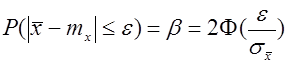. (5.8.3.)

Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 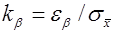. Тогда доверительный интервал для математического ожидания будет иметь вид

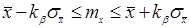или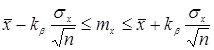

Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.

Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:

1) приближенный – при n более 50 заменяют неизвестные параметры их оценками;

2) от случайной величины a * переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра а, а зависит только от объема выборки n и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили

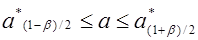Если выразить через р,

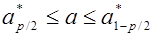На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 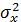неизвестна, поэтому для построения доверительного интервала математического ожидания используют выборочную дисперсию 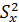и приведенную случайную величину:

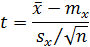
t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала

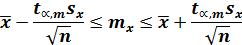
Дата добавления: 2020-12-22; просмотров: 4915; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 234 Следующая ⇒

Мы поможем в написании ваших работ!