Задания: (выполнить в практических тетрадях)

Числовые множества.

В повседневной жизни постоянно различные совокупности предметов называют одним словом. Совокупность документов называют архивом; собрание музыкантов – оркестром; группу лошадей – табуном; родителей, детей и их родственников – семьей; большую группу людей – толпой или очередью; собрание книг – библиотекой и т.д.

Математическим понятием, отражающим объединение некоторых объектов, предметов или понятий в одну единую совокупность является понятие множества. Это понятие не определяется, подобно понятиям точки, числа, и является первичным.

Предметы (объекты), составляющие некоторое множество, называются его элементами. Все множества можно записывать с помощью заглавных букв латинского алфавита:

А – множество квадратов;

В – множество чисел.

Элементы множества можно записать с помощью маленьких букв: х является элементом множества А.

Это можно записать так: х 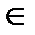А (читают: х есть элемент множества А, или х принадлежит А, или х содержится в А, или А содержит х). Если объект х не является элементом множества А, то это записывают так: х 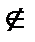А (читается: х не есть элемент множества А, или х не принадлежит А, или х не содержится в А).

Например: Если множество В – множество натуральных чисел, то 2 В, –7 В, муха 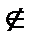В и т.д.

Множество можно задавать перечислением его элементов.

Например: множество стран на земном шаре задается их списком в географическом атласе, множество учеников в классе – их списком в классном журнале. Если множество задано списком, то названия всех элементов множества записывают в фигурные скобки, разделяя точкой с запятой.

Например: если множество С состоит из трех элементов: 1,9 и –4, то это записывают так:

С ={1;9; –4}.

Но не все множества можно записывать списком. Если множество содержит бесконечно много элементов, то такой список составить нельзя.

Множество считается заданным, если указано некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называют характеристическим свойством множества.

Множество элементов обладающих характеристическим свойством записывают так:

А = {х| х=2n, n N} означает, что множество А состоит из всех четных натуральных чисел х

Задание 1(устно):

Пусть А множество всех многочленов от одной переменной х, все коэффициенты которых целые. Верна ли запись:

а) ( – 15 х + 6) 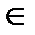А

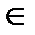б) ( х³ – 1) А

в) (х² + у² – 1) 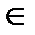А.

Далее мы будем говорить только о числовых множествах.

Давайте вспомним, какие числа вам уже знакомы из школьного курса математики. Это натуральные, целые, рациональные, иррациональные и действительные числа. Указанные числа являются элементами следующих множеств:

N – множество натуральных чисел – его элементами являются числа, которые используются при счете предметов.

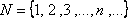
Так как множество натуральных чисел является одним из первоначальных понятий математики, то определения ему не дается. Следует помнить, что ноль не является натуральным числом.

Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течении сотен тысячелетий этого периода люди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и их энергия уходила преимущественно на добывание пищи простейшим способом – собиранием её, где только это было возможно. Пока не произошёл переход от простого собирания пищи к активному её производству, от охоты и рыболовства к земледелию, люди мало продвинулись в понимании числовых величин и пространственных отношений.

Мало-помалу сложилось первобытно-коммунистическое общество с соответствующим распределением пищи, одежды и орудия. Все эти обстоятельства вынудили человека так или иначе вести счет общего имущества, сил врага, с которым приходилось вступать в борьбу за овладение новыми территориями. Процесс счета уже не мог остановиться на четырех(поднятие обеих рук и указание на ноги) и должен был развиваться далее и далее. На этой ступени развития в математику входит первая абстракция, заключающаяся в том, что пересчитываемые предметы заменяются какими-либо другими однородными между собой предметами или знаками: камешками, узелками, ветками, зарубками. Операция производится по принципу взаимно-однозначного соответствия: каждому пересчитываемому предмету ставится в соответствие один из предметов, выбранных в качестве орудия счета (то есть один камешек, один узелок на веревке и т.д.).

Чтобы следить за своим стадом, древние пастухи делали из глины кружки - по одному на каждую овцу. Для того, чтобы узнать, не пропала ли за день хоть одна овца, пастух откладывал в сторону по кружку каждый раз, когда очередное животное заходило в загон. Но в его стаде были не только овцы, поэтому пришлось делать из глины и другие фигурки. А земледельцы с помощью глиняных фигурок вели учёт собранного урожая, отмечая, сколько мешков зерна положено в амбар, сколько кувшинов масла выжато из оливок, сколько соткано кусков льняного полотна. Так, ещё не умея считать, занимались древние люди арифметикой.

Но перекладывать каждый раз глиняные фигурки с места на место было довольно утомительным занятием. Да и при обмене рыб на каменные ножи и или антилоп на каменные топоры удобнее было сначала пересчитывать товары, а уж потом приступать к обмену. Но прошло много тысячелетий, прежде чем люди научились пересчитывать предметы. Для этого им пришлось придумать названия для чисел.

Для упрощения счета использовались различные счетные приборы, например, абак , русские счеты или сходный с ними китайский суан-пан. Абак, впервые появился, вероятно, в Древнем Вавилоне около 3 тыс. до н. э. Первоначально представлял собой доску, разграфлённую на полосы или со сделанными углублениями. Счётные метки (камешки, косточки) передвигались по линиям или углублениям. В 5 в. до н. э. в Египте вместо линий и углублений стали использовать палочки и проволоку с нанизанными камешками.

На множестве натуральных чисел можно ввести операции сложения, умножения и возведения в степень. Это означает, что результатом введенной операции будет также натуральное число. Операция вычитания может выполняться, только если уменьшаемое больше вычитаемого (или равно ему, если считать 0 натуральным числом). Операция деления возможна, если частное p и остаток r от деления a на b определяются так: a = p * b + r.

Натуральные числа можно разбить на два класса – простые и составные числа.

Определение. Натуральное число n называется простым числом, если оно не имеет других делителей, кроме единицы и самого этого числа.

Z - множество целых чисел, его элементы - это натуральные числа, числа, противоположные натуральным и ноль.

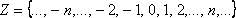
Отрицательные числа стали использоваться в математике значительно позже дробных, тем более, натуральных. В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).

В результате появления отрицательных чисел и нуля стало возможным введение операции вычитания, которая, если строго ее определить, есть операция сложения, в которой второе слагаемое заменяется противоположным по знаку: .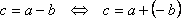

Q – множество рациональных чисел, состоящее из чисел, которые можно представить в виде несократимой дроби вида р – целое, q - натуральное .

Определив понятие рационального числа в виде дроби, можно ввести операцию деления на множестве рациональных чисел, как умножения на обратное число:

Из курса математики хорошо известны правила выполнения основных арифметических действий над рациональными числами:

и , тогда

1) ,

2) ,

3) ,

4) .

R – множество действительных чисел, элементы которого – либо рациональные, либо иррациональные числа.

Любое иррациональное число можно записать в виде бесконечной непериодической дроби, и любая непериодическая дробь является иррациональным числом (примеры).

Если мы представим данные множества в виде кругов, то, конечно, эти круги будут неравными. Такие круги называются Кругами Эйлера и выглядят вот так (рис. 1)

Операции над множествами.

Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .

Говорят, что множество А содержится в множестве В ( рис.1 ) или множество А является подмножеством множества В ( в этом случае пишут А ⸦ В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: А и А ⸦ А

Сумма ( объединение ) множеств А и В ( пишется А В ) есть множество элементов, каждый из которых принадлежит либо А , либо В. Таким образом, є А В тогда и только тогда, когда либо є А , либо є В .

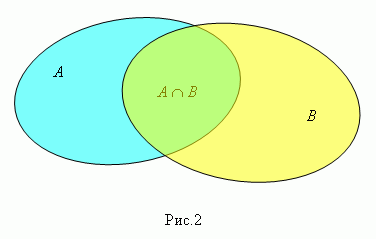
Произведение ( пересечение ) множеств А и В ( пишется А∩ В , рис.2 ) есть множество элементов, каждый из которых принадлежит и А , и В . Таким образом, є А В тогда и только тогда, когда є А и є В .

Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением будет отрезок [1, 4], пересечением - отрезок [2, 3], разностью A\B - полуинтервал [1, 2), B\A - полуинтервал (3, 4].

Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда есть множество всех квадратов, A\B - множество прямоугольников с неравными сторонами, B\A - множество всех ромбов с неравными углами.

Пример 3. Пусть A = {1, 2, 3, 4, 5, 6, 7, 8, 9} и B = {1, 3, 5, 7, 9, 11, 13, 17, 19}. Найти и объединение и пересечение данных множеств.

= {1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 17, 19},

= {1, 3, 5, 7, 9}.

Пример 4. Пусть A = [−2; 1] и B = (0; 3). Найти и объединение и пересечение данных множеств.

= [−2; 3), = (0; 1].

Задания: (выполнить в практических тетрадях)

1. найти пересечение и объединение множеств A={1,4,7,8,9,12} B={1,3,7,9,10,12}.

2. найти пересечение A={3, 1, 7, 12, 5, 2}, B={1, 0, 2, 12}, D={7, 11, 2, 1, 6}, E={1, 7, 15, 8, 2, 6}

3. Найдите пересечение и объединение множеств A=(−∞, −15)∪{−5}∪[0, 7]∪{12} и B=(−20, −10)∪{−5}∪(2, 3)∪{17}.

Дата добавления: 2020-12-22; просмотров: 60; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!