Определение истинных положений поршня при повороте кривошипа с учётом поправки Брикса.

На развёрнутой индикаторной диаграмме по оси абцис откладывается в масштабе величины хода поршня при повороте на какой -то угол. Известно, что между поворотом кривошипа и ходом поршня нет прямой пропорциональности, т.е. при повороте кривошипа на 45° поршень пройдёт меньше или больше четверти хода, а при повороте на 90° - меньше или больше половины хода поршня. Это в первые установил французский инженер Брикс и ввел необходимую поправку.

Истинные положения поршня при повороте кривошипа через каждые 15°, с учётом поправки Брикса, определяют следующим образом:

Определяется истинная величина поправки Брикса – ОО₁ в масштабе

                       λ

R – радиус кривошипа в масштабе, равный ½

                                   R =  мм

λ – выбирается в разделе диаграмма «время сечение», λ =

                                  

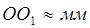
На диаграмме участок в пуска делится пополам и из центра О, радиусом R описывается полуокружность.

Вправо от центра О поправка Брикса ОО₁; из центра О₁ описывается малая полуокружность произвольным радиусом, меньшим R.Эта малая полуокружность делится на 12 малых частей

Из центра ОО₁ проводится через зафиксированные точки радиусы до пересечения с большой полуокружностью и наносятся численные значения.

Из точек пересечения опускаются перпендикуляры, которые фиксируют на оси абцис истинное положение поршня при повороте кривошипа через каждые 15°

Для того чтобы разметить горизонтальную ось всей диаграммы через 15° с учётом поправки Брикса необходимо, установив ножу измерителя в точку 180° , «перекидывать» величины отрезков от 165° до 0° и фиксировать их сжатия. При этом следует учитывать, что разметка будет одинаковой при движении поршня вниз, т.е. на тактах впуска и расширения и при движении поршня вверх, т.е. на тактах сжатия и выпускаю

Поправка Брикса – поправка на конечную длину шатуна. Если – бы шатун имел бесконечную длину (L = ∞) , то поправка Брикса равнялась бы нулю.

                                    

т.е. между поворотом кривошипа и ходом поршня была бы прямая пропорциональность. Следовательно, в этом случае при повороте кривошипа на каждые 15° поршень проходил бы одинаковые расстояния.                       

Построение диаграммы сил инерции (диаграммы Толле)

По законам кинематики кривошипно – шатунного механизма (КШМ) поршень и верхняя часть шатуна, совершая поступательное движение движется не равномерно – то с ускорением, то с замедлением. Следовательно, всё время будут возникать силы инерции поступательно движущихся масс.

Математическое выражение силы инерции в общем виде при поступательном движении

                                   Р_и = -м * а

М – масса; она определяется как вес тела G, поделенный на ускорение свободного падения g = 9,8м/сек²

                                   М = G/9,8

В КШМ силы инерции в ВМТ и НМТ   будут не равными из – за влияния конечной длины шатуна

                                    

В поступательном движении участвуют масса поршня в комплекте с кольцами, пальцем и 40% массы шатуна.

            М = G_{поршня(кг)} / 981 (см/сек²)+0,4G(_{шатуна)}/981(кг/сек²)

Вес поршня и шатуна выбирается по данным прототипа.

Принимаю G_поршня = кг

              G_шатуна =  кг

                   М = кг/сек²

R – истинный радиус кривошипа проектируемого дизеля (см )  

R = см.

ω – угловая скорость ( 1/сек )

                                  ω =π * n / 30

n – частота вращения проектируемого дизеля ( об/ мин ) n = 450 об/мин

                     ω =  (1 / сек)

λ = R / L – принята ранее при определении поправки Брикса

λ =1 / 4

Для получения движущей силы Р_g необходимо сложить силу давления газов P_r и силу инерции Р_и

                                   P_g = P_r + Р_и

Р_г – измеряется в кгс/см², Р_и нужно получить тоже в кгс/см². Полученную величину нужно разделить па площадь

                          M/F либо G/F

F (см2) – площадь поршня проектируемого дизеля.

                                     

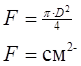
D (см2) – диаметр проектируемого дизеля

           

D (см2) – диаметр проектируемого дизеля

      

Полученные значения в кгс/см² переводятся в линейные величины

(1 кгс/см² - 2мм)

            Р_и (вмт) * m=  мм =АС

            Р_и(нмт) *  m мм = ВД

Построение диаграммы Толле.

1. на концах отрезка АВ равного длине индикаторной диаграмме I откладываются величины АС – вверх, ВД - вниз

точки С и Д соединяются прямой линией и из точки пересечения E

откладывается вниз отрезок

                  

точка F соединяется прямыми линиями с точками С и Д; полученные отрезки CF и FД делятся на одинаковое число (8) равных частей.

2. Одноимённые точки соединяются прямыми линиями. К этим линиям проводится касательная, которая и будет являться кривой сил инерции поступательного движения масс.

3. Полученная диаграмма показывает, что наибольших значений силы инерции достигают в мёртвых точках (АС – ВМТ, ВД - НМТ). В районе среднего ход поршня силы становятся равными и теряют своё направление. В первой половине хода поршня силы инерции препятствуют движению, а во второй – помогают.

 

---

Дата добавления: 2020-04-08; просмотров: 936; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!